Взаимодействия среды

Без опции Symbolic функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.

Пример 1

Уравнения и переменные могут быть введены как наборы или списки:

numeric::linsolve({x = y - 1, x + y = z}, {x, y});
numeric::linsolve([x = y - 1, x + y = z], {x, y});
numeric::linsolve({x = y - 1, x + y = z}, [x, y]);
numeric::linsolve([x = y - 1, x + y = z], [x, y])

С опцией Symbolic используется точная арифметика. Следующая система имеет набор с 1 параметром решения; неизвестный x ₃ произволен:

numeric::linsolve([x[1] + x[2] = 2, x[1] - x[2] = 2*x[3]],
                  [x[1], x[2], x[3]], Symbolic)

Неизвестные могут быть выражениями:

numeric::linsolve([f(0) - sin(x + 1) = 2, f(0) = 1 - sin(x + 1)],
                  [f(0), sin(x + 1)])

Следующая система не имеет решения:

numeric::linsolve([x + y = 1, x + y = 2], [x, y])

Пример 2

Мы демонстрируем некоторые примеры с символьными коэффициентами. Обратите внимание на то, что опция Symbolic должна использоваться:

eqs := [x + a*y = b, x + A*y = b]:
numeric::linsolve(eqs, [x, y], Symbolic)

Обратите внимание на то, что для a = A, это не общее решение. Используя опцию ShowAssumptions, оказывается, что вышеупомянутым результатом является общее решение, подвергающееся предположению a ≠ A:

numeric::linsolve(eqs, [x, y], Symbolic, ShowAssumptions)

delete eqs:

Пример 3

Мы даем дальнейшую демонстрацию опции ShowAssumptions. Следующая система не имеет решения для всех значений параметра a:

numeric::linsolve([x + y = 1, x + y = a], [x, y], Symbolic)

С ShowAssumptions numeric::linsolve занимается расследованиями под который условия (на параметре a) существует решение:

numeric::linsolve([x + y = 1, x + y = a], [x, y], Symbolic,
                  ShowAssumptions)

Мы приходим к заключению, что существует набор с 1 параметром решений для a = 1. Ограничение в a является линейным уравнением, начиная с параметра, a вводит уравнения линейно. Если a рассматривается как неизвестное, а не в качестве параметра, ограничение становится частью решения:

numeric::linsolve([x + y = 1, x + y = a], [x, y, a], Symbolic,
                  ShowAssumptions)

Пример 4

С точной арифметикой PI рассматривается как символьный параметр. Следующая система имеет решение, подвергающееся ограничению PI = 1:

numeric::linsolve([x = x - y + 1, y = PI], [x, y],
                  Symbolic, ShowAssumptions)

С арифметикой с плавающей точкой PI преобразован в 3.1415.... Система не имеет никакого решения:

numeric::linsolve([x = x - y + 1, y = PI], [x, y], 
                  ShowAssumptions)

Пример 5

Поскольку numeric::linsolve не делает систематической внутренней проверки на нелинейность, пользователь должен убедиться, что уравнения, которые будут решены, действительно линейны в неизвестных. В противном случае странные вещи могут произойти. Мусор производится для следующих нелинейных систем:

a := sin(x):
numeric::linsolve([y = 1 - a, x = y], [x, y], Symbolic)

numeric::linsolve([a*x + y = 1, x = y], [x, y], Symbolic)

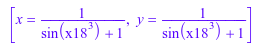
Полиномиальная нелинейность обычно обнаруживается. Относительно x, y, c как неизвестные следующая квадратичная система приводит к ошибке:

numeric::linsolve([x*c + y = 1, x = y], Symbolic)

Error: This system does not seem to be linear. [numeric::linsolve]

 Error:
This system does not seem to be linear. [numeric::linsolve] 

Эта система линейна в x, y, если c расценивается в качестве параметра:

numeric::linsolve([x*c + y = 1, x = y], [x, y], Symbolic)

delete a:

Пример 6

Мы решаем большую разреженную систему. Матрица коэффициентов имеет только 3 диагональных полосы. Обратите внимание на то, что оба уравнения, а также переменные передаются как списки. Это гарантирует, что структура полосы не потеряна внутренне:

n := 500: x[0] := 0: x[n + 1] := 0:
eqs := [x[i-1] - 2*x[i] + x[i+1] = 1 $ i = 1..n]:
vars := [x[i] $ i = 1..n]:
numeric::linsolve(eqs, vars)

Структура полосы потеряна, если уравнения или неизвестные заданы наборами. Следующий вызов занимает больше времени, чем предыдущий вызов:

numeric::linsolve({op(eqs)}, {x[i] $ i = 1..n})

delete n, x, eqs, vars:

Пример 7

Symbolic опции не должен использоваться для уравнений с коэффициентами с плавающей точкой, потому что символьная вертящаяся стратегия способствует эффективности вместо числовой устойчивости.

eqs := [x + 10^20*y = 10^20, x + y = 0]:

Приближение плавающее точного решения:

map(numeric::linsolve(eqs, [x, y], Symbolic), map, float)

Мы теперь преобразовываем точные коэффициенты в числа с плавающей запятой:

feqs := map(eqs, map, float)

Значение по умолчанию, вертящееся стратегия, стабилизирует операции с плавающей точкой. Следовательно, каждый получает правильный результат:

numeric::linsolve(feqs, [x, y])

С Symbolic вертящаяся стратегия оптимизирует скорость, принимая точную арифметику. Числовая нестабильность может произойти, если коэффициенты с плавающей точкой включены. Следующий неправильный результат вызывается внутренними эффектами округления (“отмена”):

numeric::linsolve(feqs, [x, y], Symbolic)

delete eqs, feqs:

Пример 8

Мы демонстрируем, что упрощенные уравнения, представляющие решение, могут использоваться для последующей обработки с subs:

eqs := [x + y = 1, x + y = a]:
[Solution, Constraints, Pivots] := 
  numeric::linsolve(eqs, [x, y], ShowAssumptions)

subs(eqs, Solution)

Решение может быть присвоено неизвестным через assign:

assign(Solution):
x, y, eqs

delete eqs, Solution, Constraints, Pivots, x:

Пример 9

Если решение линейной системы не уникально, то некоторые неизвестные используются в качестве “свободных параметров” охват пробела решения. В следующем примере, неизвестные z, w такие параметры. Они не поднимаются на левой стороне решенных уравнений:

eqs := [x + y = z, x + 2*y = 0, 2*x - z = -3*y, y + z = 0]:
vars := [x, y, z, w]:
Solution := numeric::linsolve(eqs, vars, Symbolic)

Можно задать функцию, такую как следующий NewSolutionList, чтобы переименовать свободные параметры к “myName1”, “myName2” и т.д. и заполнить список решенных уравнений соответственно:

NewSolutionList := 
proc(Solution : DOM_LIST, vars : DOM_LIST, myName : DOM_STRING)
local i, solvedVars, newEquation;
begin
  solvedVars := map(Solution, op, 1);
  for i from 1 to nops(vars) do
     if not has(solvedVars, vars[i]) then
        newEquation := vars[i] = genident(myName);
        Solution := listlib::insertAt(
            subs(Solution, newEquation), newEquation, i) 
     end_if 
  end_for:
  Solution
end_proc:

NewSolutionList(Solution, vars, "FreeParameter")

delete eqs, vars, Solution, NewSolutionList:

Пример 10

Мы демонстрируем различие между аппаратной и программной арифметикой. Следующая проблема очень плохо обусловлена. Результаты, оба с HardwareFloats, а также с SoftwareFloats, омрачены числовым округлением:

n:= 10:
eqs:= [(_plus(x[j]/(i + j -1) $ j = 1..n) = 1) $ i = 1..n]:
vars:= [x[i] $ i = 1..n]:
numeric::linsolve(eqs, vars, SoftwareFloats);
numeric::linsolve(eqs, vars, HardwareFloats)

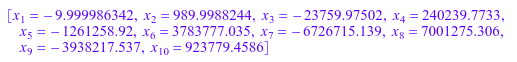
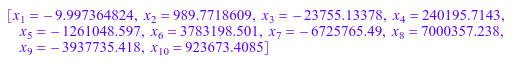
Это - точное решение:

numeric::linsolve(eqs, vars, Symbolic);

delete eqs, vars:

Пример 11

Мы демонстрируем, как полное решение следующей линейной системы в x, y с символьными параметрами a, b, c, d может быть найден:

eqs := [x + y = d, a*x + b*y = 1, x + c*y = 1]:
numeric::linsolve(eqs, [x, y], Symbolic, ShowAssumptions)

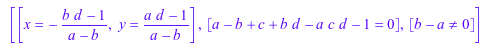
Это - общее решение, принимая a ≠ b. Мы теперь устанавливаем b = a исследовать дальнейшие ответвления решения:

eqs := subs(eqs, b = a):
numeric::linsolve(eqs, [x, y], Symbolic, ShowAssumptions)

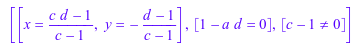
Это - общее решение для a = b, принимая c ≠ 1. Мы наконец устанавливаем c = 1 получать последнее ответвление решения:

eqs := subs(eqs, c = 1):
numeric::linsolve(eqs, [x, y], Symbolic, ShowAssumptions)

От ограничений на символьные параметры a и d, мы приходим к заключению, что существует специальное решение с 1 параметром x = 1 - y для a = b = c = d = 1.

delete eqs:

Возвращаемые значения

Без опции ShowAssumptions возвращен список упрощенных уравнений. Это представляет общее решение системы eqs. FAIL возвращен, если система не разрешима.

С ShowAssumptions список возвращен [Solution, Constraints, Pivots]. Solution является списком упрощенных уравнений, представляющих общее решение eqs. Списки Constraints и Pivots содержат уравнения и неравенства, вовлекающие символьные параметры в eqs. Внутренне, они были приняты, чтобы сохраняться при решении системы.

[FAIL, [], []] возвращен, если система не разрешима.