числовой::Числовое приближение сумм (атрибут Плавающий Суммы)
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
numeric::sum(f(x),x = a .. b) numeric::sum(f(x),x in {x1, x2, …}) numeric::sum(f(x),x = {x1, x2, …}) numeric::sum(f(x),x in RootOf(p(X), X)) numeric::sum(f(x),x = RootOf(p(X), X)) float(hold(sum)(f(x),x = a .. b)) float(hold(sum)(f(x),x in {x1, x2, …})) float(hold(sum)(f(x),x = {x1, x2, …})) float(hold(sum)(f(x),x in RootOf(p(X), X))) float(hold(sum)(f(x),x = RootOf(p(X), X))) float(freeze(sum)(f(x),x = a .. b)) float(freeze(sum)(f(x),x in {x1, x2, …})) float(freeze(sum)(f(x),x = {x1, x2, …})) float(freeze(sum)(f(x),x in RootOf(p(X), X))) float(freeze(sum)(f(x),x = RootOf(p(X), X)))
numeric::sum(f(i), i=a..b) вычисляет числовое приближение
.
numeric::sum(f(x), x ∈ {x1, x2, …}) вычисляет числовое приближение
.
numeric::sum(f(x), x in RootOf(p(X), X)) вычисляет числовое приближение
.
Вызов numeric::sum(…) эквивалентен вызову атрибута float sum через float ( hold( sum )(…)) или float ( freeze( sum )(…)).
Если существуют другие символьные параметры в f (x) кроме переменной x суммирования, символьная сумма возвращена. Числовые выражения такой как
,
и т.д. приняты и преобразованы в числа с плавающей запятой.
За бесконечные суммы выражение f (i) с целочисленным i должен иметь дополнительный f (x) ко всему действительному x в интервале
. Внутренне, интеграл
вычисляется численно и используется в процессе приближения.
За конечные суммы numeric::sum только возвращает _plus ( float(f(i)$i=a..b)). Обратите внимание на то, что числовая отмена может произойти! Если f(i) не содержит числа с плавающей запятой, отмены может избежать, суммировав символьные условия _plus(f(i)$i=a..b) вместо этого. Cf. Пример 3.
Сходимость быстра, если f (x) затухает быстро для x -> infinity или | x | -> infinity, соответственно
Сходимость может быть медленной для чередования сумм, содержащих выражения такой как (-1) i. Такие суммы также часто подвергаются проблемам отмены!
Вызов numeric::sum(f(x), x = {x1, x2, …}) вычисляет числовые приближения x1, x2 и т.д., заменяет этими значениями в f (x) и складывает результаты. Этот процесс может подвергнуться проблемам отмены!
Вызовы numeric::sum(f(x), x ∈ {x1, x2, …}) и numeric::sum(f(x), x = {x1, x2, …}) эквивалентны.
Вызов numeric::sum(f(x), x in RootOf(p(X), X)) вычисляет числовые приближения всех корней p, заменяет этими значениями в f (x) и складывает результаты. Cf. Пример 4. Этот процесс может подвергнуться проблемам отмены!
Вызовы numeric::sum(f(x), x in RootOf(p(X), X)) и numeric::sum(f(x), x = RootOf(p(X), X)) эквивалентны.
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы демонстрируем некоторые эквивалентные призывы к числовому суммированию:
numeric::sum(1/i!, i = 0..infinity), float(hold(sum)(1/i!, i = 0..infinity)), float(freeze(sum)(1/i!, i = 0..infinity))
MuPAD® символьное суммирование sum не находит простое представление следующей суммы:
sum(1/i!/(i^2+1)!, i = 0..infinity)
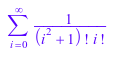
Следующая оценка плавающая вызывает numeric::sum:
float(%)
Точное значение следующей суммы является π coth (π):
numeric::sum(1/(1+i^2), i = -infinity..infinity) = float(PI*coth(PI))
Следующая сумма не может быть оценена численно из-за символьного параметра x:
numeric::sum(1/(x+i^2), i = -infinity..infinity)
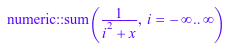
Мы демонстрируем числовую отмену при подведении итогов Ряда Тейлора для
:
exp(-20.0) <> numeric::sum((-20)^i/i!, i = 0..100)
Также бесконечная сумма страдает от отмены:
exp(-20.0) <> numeric::sum((-20)^i/i!, i = 0..infinity)
Отмена может избегаться использования конечная сумма с точными условиями:
exp(-20.0) = float(_plus((-20)^i/i! $ i = 0..100))
Следующий вызов вычисляет числовые корни полинома в выражении RootOf и суммах по всем корням:
numeric::sum(exp(x)/x, x in RootOf(X^10 - X - PI, X))
| |
|
Переменные суммирования: идентификаторы или индексированные идентификаторы |
|
Целые числа или ± |
|
Числовые выражения |
|
Одномерное многочленное выражение в X |
|
Неопределенный из p: идентификатор или индексируемый идентификатор |
Число с плавающей точкой или символьное выражение типа numeric::sum.
В зависимости от того, чередуется ли ряд или монотонность, numeric::sum пробует много стратегий вычислить его предел: u преобразование Левина, формула Эйлера-Маклаурина или прием ван Виджнгэардена.
Формула Эйлера-Маклаурина
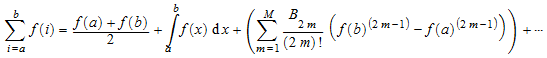
включение Бернуллиевых чисел B 2 m.