Пример 1

plot::easy пытается преобразовать все определенные данные и выражения в допустимые графические объекты и атрибуты:

plot::easy(sin(x), [PI/2,1])

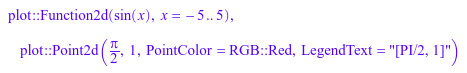
Поскольку функциональный plot вызывает функциональный plot::easy для предварительной обработки его входных данных, сцены как вышеупомянутое могут непосредственно быть построены с помощью plot:

plot(sin(x), [PI/2,1], #x = PI/2, #y = 1)

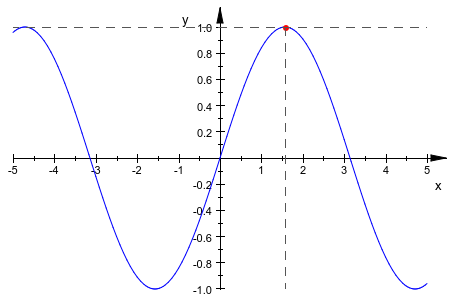
Теперь, это - только небольшой шаг, чтобы анимировать эту сцену:

plot(sin(x), {[x,sin(x)], #Points}, #x = x, #y = sin(x))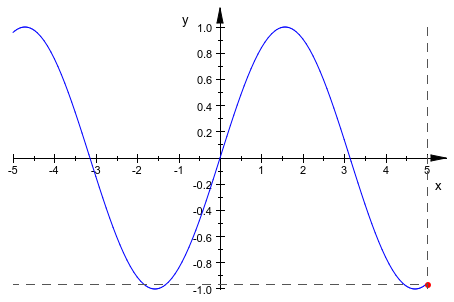

Примечание: Графические объекты и атрибуты, а также данные, которые не может преобразовать plot::easy, возвращены неизменные:

plot::easy(x, plot::Point2d(1,1), LineStyle=Dashed, "UnknownObject")

Поэтому plot возвращает следующее сообщение об ошибке, когда это выполняется с вышеупомянутыми аргументами:

plot(x, plot::Point2d(1,1), LineStyle=Dashed, "UnknownObject");

Error: Invalid arguments '"UnknownObject"'. [plot::Canvas::new]

Пример 2

Точки могут быть введены как списки с двумя или тремя значениями. Также соответствующий вектор-столбец в сочетании с опцией #Points (искажают #P, смотрите, Пример 18) может использоваться.

Обратите внимание на то, что для графического вывода анимированных точек опция #Points требуется. В противном случае кривая (когда вводится список) или стрелка (когда вводится вектор) построена:

plot([0,1], [s,s^2], {[s,s^2], #Points}, s = -2.. 2,
     matrix([t,t^2]), {matrix([t,t^2]), #Points}, t = 2..-2
)

Смотрите также: plot::Point2d, plot::Point3d.

Пример 3

Стрелки могут быть заданы как вектор-столбцы с двумя или тремя элементами. Также список в сочетании с опцией #Arrows (искажают #A, смотрите, Пример 13) может использоваться:

plot(matrix([0,1]), matrix([s,s^2]), s = 2..-2,
     [t,t^2], {[t,t^2], #Arrows}, t = -2..2
)

Если стрелка должна запуститься в координатах кроме (0,0) или (0,0,0), соответственно, то список двух вектор-столбцов или соответствующий список списков в сочетании с опцией #Arrows (искажают #A, смотрите, Пример 13) может использоваться:

u := matrix([3,2]):
v := matrix([1,4]):
w := (1-a)*u + a*v:
u, v, w;

plot(u, v, [u,w], a = 0.1..1, #Arrows)

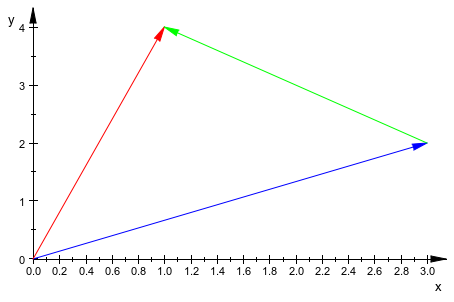
delete u, v, w:

Смотрите также: plot::Arrow2d, plot::Arrow3d.

Пример 4

Полигоны могут быть заданы как списки, таблицы или матрицы. В следующем примере полигоны построены с помощью различных входных стилей. Опция #Origin (искажают #O, смотрите, Пример 17) гарантирует, что источник системы координат видим в сцене также:

plot([[1,3],[2,5],[3,3],[4,8]],
     table(1=4,2=6,3=4,4=9),
     [matrix([1,5]),matrix([2,7]),matrix([3,5]),matrix([4,10])],
     matrix([[1,6],[2,8],[3,6],[4,11]]),
     #Origin)

Обратите внимание на то, что полигоны отображены как точки, когда опция #Points (искажают #P, смотрите, Пример 18) используется:

plot([[1,3],[2,5],[3,3],[4,8]],
     table(1 = 4,2 = 6,3 = 4,4 = 9),
     [matrix([1,5]),matrix([2,7]),matrix([3,5]),matrix([4,10])],
     matrix([[1,6],[2,8],[3,6],[4,11]]),
     #Points, #Origin)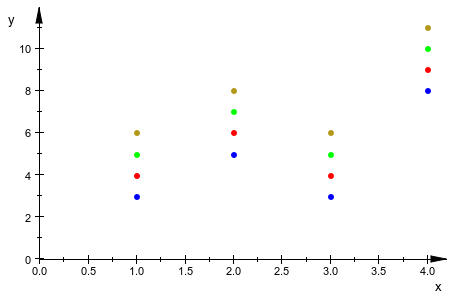

Обратите внимание на то, что следующие полигоны с двумя элементами отображены как стрелки, когда опция #Arrows (искажают #A, смотрите, Пример 13) используется:

plot([[1,4],[2,6]],
     [matrix([1,5]),matrix([2,7])],
     matrix([[1,6],[2,8]]),
     #Arrows, #Origin)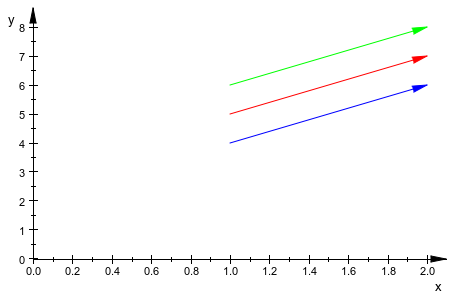

Смотрите также: plot::Polygon2d, plot::Polygon3d.

Пример 5

Укажите, что списки могут быть заданы как списки, таблицы или матрицы. Для каждой точки должен быть задан цвет RGBa. В следующем примере списки точек построены с помощью различных входных стилей. Опция #Origin (искажают #O, смотрите, Пример 17) гарантирует, что источник системы координат видим в сцене также:

plot([[1,2,RGB::Red], [2,4,[0,1,0]], [3,3,[0,0,1,0.5]]],
     [matrix([1,3,RGB::Red]), matrix([2,5,[0,1,0]]), 
                              matrix([3,4,[0,0,1,0.5]])],
     matrix([[1,4,RGB::Red], [2,6,[0,1,0]],[3,5,[0,0,1,0.5]]]),
     table(1=[5,RGB::Red], 2=[7,[0,1,0]], 3=[6,[0,0,1,0.5]]),
     #Origin)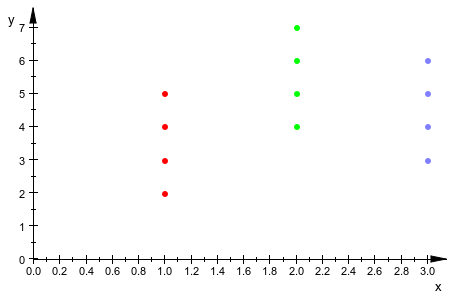

Обратите внимание на то, что списки следующих моментов отображены как стрелки, когда опция #Arrows (искажают #A, смотрите, Пример 13) используется:

plot([[1,2,RGB::Red], [2,4,[0,1,0]] ,[3,3,[0,0,1,0.5]]],
     [matrix([1,3,RGB::Red]), matrix([2,5,[0,1,0]]), 
                             matrix([3,4,[0,0,1,0.5]])],
     matrix([[1,4,RGB::Red], [2,6,[0,1,0]], [3,5,[0,0,1,0.5]]]),
     table(1=[5,RGB::Red], 2=[7,[0,1,0]] ,3=[6,[0,0,1,0.5]]),
     #Arrows, #Origin)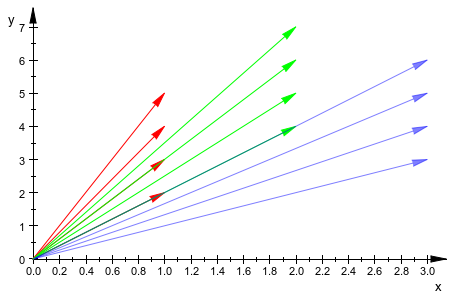

Смотрите также: plot::PointList2d, plot::PointList2d.

Пример 6

Для проведения горизонтали и вертикальных бесконечных линий, короткий синтаксис #x = e и #y = e с e являются действительным выражением, может использоваться:

plot(sin(x), [PI/2,1], #x=PI/2, #y=1, #Legend)

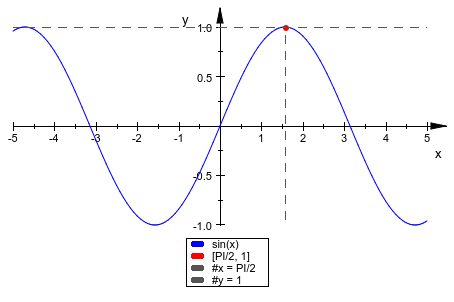
Для рисования горизонтали и вертикальных бесконечных плоскостей, короткого syntax#x = e, #y = e и #z = e, с e действительное выражение, может использоваться.

Оба, строки и плоскости могут также быть анимированы:

plot([t,0,t^2], {[t,0,t^2], #Points}, #x=t, #z=t^2, #Legend)

Смотрите также: plot::Line2d, plot::Plane.

Пример 7

Кривая может быть задана как список с двумя или тремя элементами, где по крайней мере один элемент зависит от свободной переменной. Если опция #Points (искажают #P, смотрите, Пример 18) установлен, то вместо кривой, анимированная точка построена, который проходит кривая.

plot([t,sin(t)], {[t,sin(t)], #Points},  t=0..2*PI)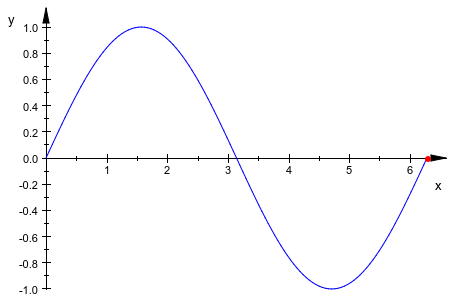

Смотрите также: plot::Curve2d, plot::Curve3d.

Пример 8

plot::easy пытается преобразовать выражения, которые не являются никакими списками, наборами, матрицами, уравнениями или неравенствами в графики 2D или 3D функций. Мы строим некоторые графики 2D функций:

plot(sin(x), tan(x), x)

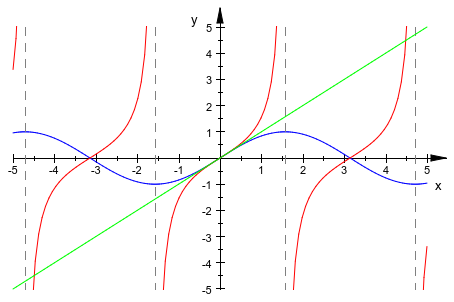
Мы строим простую 3D функцию. Обратите внимание на то, что опция #3D (искажают #3, смотрите, Пример 12) требуется в следующем примере для графического вывода 3D функции. В противном случае анимированная 2D функция создается.

plot(m*x, #3D)

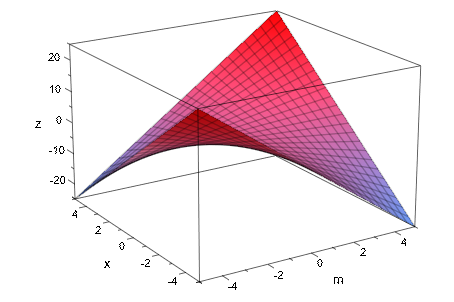
Мы строим простую 2D анимацию: точка и соответствующая касательная синусоидальной функции проходят график синусоидальной функции:

f:= x -> sin(x):
plot(f(x), x = -PI..PI,
     {[a, f(a)], #Points}, f'(a)*(x-a) + f(a), a = -PI/2..PI/2)

Мы строим кусочную заданную функцию:

plot(piecewise([x < 1, -x^2 + 1], [x >= 1, x + 5]), #x=1, #Legend)

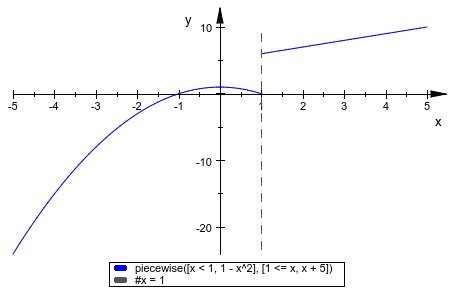
Та же кусочная заданная функция теперь написана в более коротком синтаксисе. Отметьте различие между определением одной функции с двумя ответвлениями (слева) и определением двух функций (справа):

plot({{[[x < 1, -x^2 + 1], [x >= 1, x + 5]], #x=1}},
     {{ [x < 1, -x^2 + 1], [x >= 1, x + 5] , #x=1}},
     #Legend)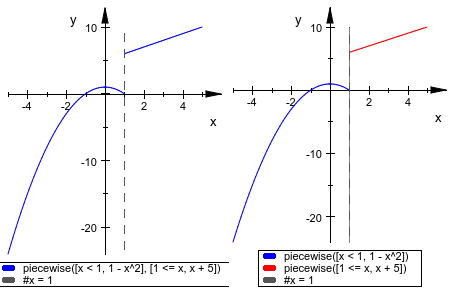

Смотрите также: plot::Function2d, plot::Function3d.

Пример 9

Неявная функция может быть задана как уравнение:

plot(u^5 + x^2 = 1 - u^3)

Обратите внимание на то, что опция #3D (искажают #3, смотрите, Пример 12) может потребоваться, чтобы строить плоскости, данные как декартовы уравнения. В противном случае анимированный 2D график может быть создан. Это зависит от количества переменной уравнения.

E1:= 2*x + 30*y - 2*z = 5:
E2:= -x + 7*y - z = 12:
E3:= -4*x + 2*y + z = 0:
plot(E1, E2, E3, #3D, #Legend)

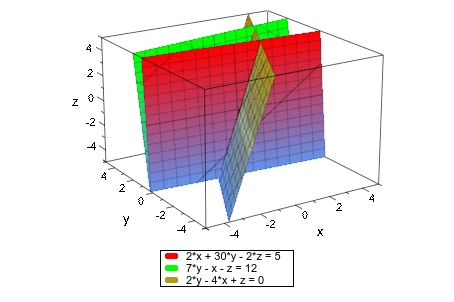
delete E1, E2, E3:

Смотрите также: plot::Implicit2d, plot::Implicit3d.

Пример 10

Неравенство может быть отображено непосредственно:

plot(u^5+x^2 < 1-u^3)

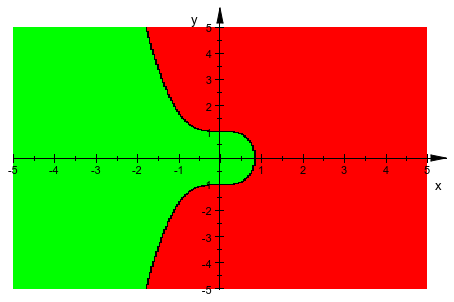
То же самое верно для списка неравенств и уравнений:

plot([x < 3, x > 1, y <  4, y > -4])

Смотрите также: plot::Inequality.

Пример 11

Чтобы отобразить 2D текст в определенном положении, уравнение координатного кортежа и символьной строки или процедуры может быть введено:

plot([t, t^2],
    {[t, t^2], #Points},
     [t, t^2] = "moving text")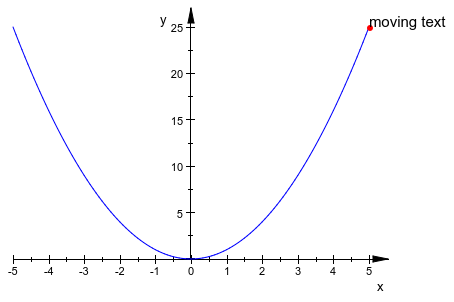

Мы отображаем 3D текст. Как в любом другом контексте plot::easy, мы можем использовать регулярные графические атрибуты как TextFont =Center также:

DIGITS := 2:
plot([t, t^2, 1],
    {[t, t^2, 1], #Points},
     [t, t^2, 1] = (t->" x = ".[t, t^2, 1.0]),
     TextFont=[Bold]):
delete DIGITS: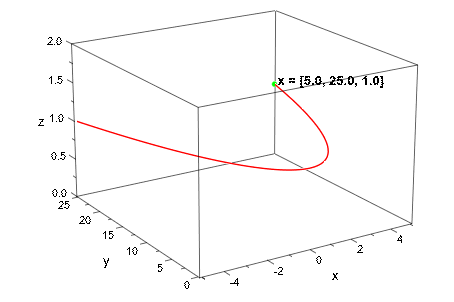

Смотрите также: plot::Text2d, plot::Text3d.

Пример 12

Обычно plot::easy создает 2D сцену, если один из аргументов не является 3D объектом или может только быть преобразован к 3D объекту или опции, #3D используется.

plot(sin(x), #3)

Однако опция #3D является только подсказкой. Это проигнорировано, если текущая сцена может только быть 2D сценой. В следующем примере 2D точка определяет размерность сцены:

plot([PI/2,1], sin(x), #3)

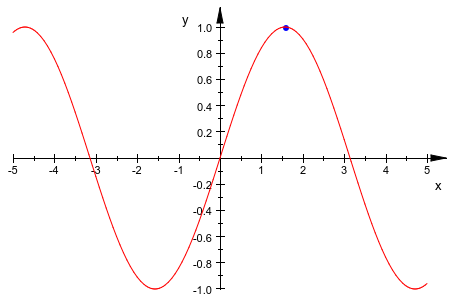
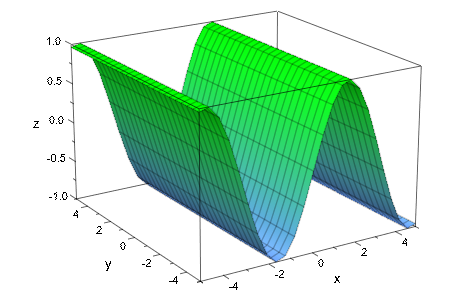
В следующем примере 3D точка определяет размерность сцены. Нет никакой потребности использовать опцию #3D в порядке создать 3-ю сцену:

plot([PI/2,1,0], sin(x))

Пример 13

С опцией создаются #Arrows, стрелки вместо точек или кривых. Когда используется в {...} - группа, это влияет на элементы этой группы или сцены только.

plot({{ [-5,25], [5,25], [x,x^2]     }},
     {{ [-5,25], [5,25], [x,x^2], #A }})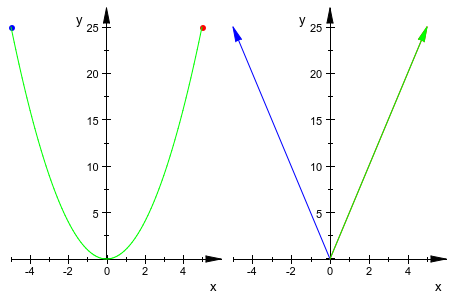

Пример 14

Опция #Constrained создает систему координат с ограниченными масштабированными осями. Это - ярлык для Scaling = Constrained.

plot({{ x^2 }}, {{ x^2, #C }})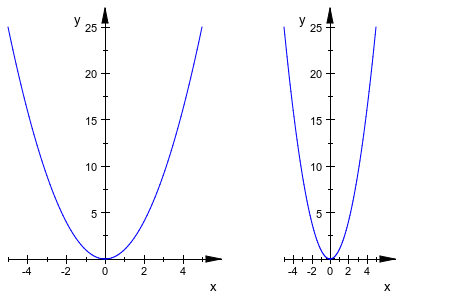

Пример 15

Опция #Grid создает систему координат с линиями сетки. Это - ярлык для GridVisible = TRUE.

plot({{ x^2 }}, {{ x^2, #G }})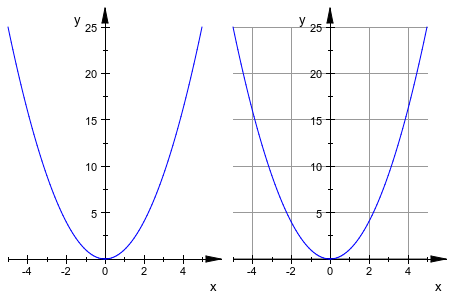

Пример 16

Опция #Legend создает легенду. Это - ярлык для LegendVisible = TRUE в сочетании с LegendEntry = TRUE. Обратите внимание на то, что plot::easy явным образом устанавливает текст легенды для каждого графического объекта, который он создает.

plot([0,-6], x^2-5, [t,t^2], #L)

Пример 17

Опция #Origin включает координаты (0,0) или (0,0,0), соответственно, в поле просмотра текущей сцены.

plot({{[2,2], [3,3]}}, {{[2,2], [3,3], #O}})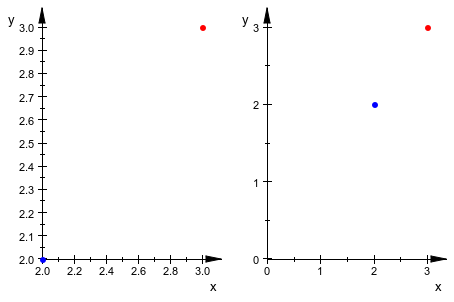

Пример 18

Используя опцию создаются #Points, точки вместо стрелок или кривых. Кроме того, эта опция устанавливает атрибуты PointsVisible =TRUE и LinesVisible =FALSE. Когда используется в {...} - группа, это влияет на элементы этой группы или сцены только.

plot({[-5,25], [x,x^2], #Gray}, {matrix([5,25]), [x,x^2], #P})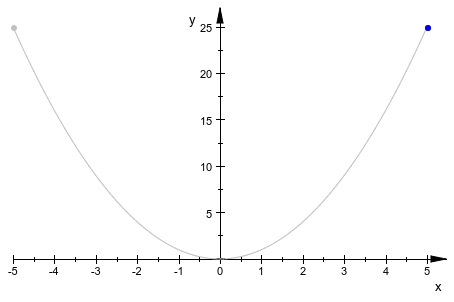

Пример 19

#X / #Y / #Z = a..b устанавливает x-/y-/z-область-значений поля просмотра сцены к a..b. Это - ярлык для ViewingBoxXRange / ViewingBoxYRange / ViewingBoxZRange = a..b.

plot({{x^2, sin(x)}}, {{x^2, sin(x), #Y=0..4}})

Мы чертим 3D сцену с ограниченным полем просмотра. Поэтому только четверть доли видима:

plot({{plot::Sphere(1)}},
     {{plot::Sphere(1), #X=0..1, #Y=0..1, #Z=0..1}})

Возвращаемые значения

Последовательность графических объектов и графических атрибутов, а также объектов, которые не могли быть преобразованы plot::easy.

Перегруженный

arg