plotfunc2dГрафики функций в 2D
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
plotfunc2d(f1, f2, …, <Colors = [c1, c2, …]>, <attributes>) plotfunc2d(f1, f2, …,x = xmin .. xmax, <Colors = [c1, c2, …]>, <attributes>) plotfunc2d(f1, f2, …,x = xmin .. xmax,a = amin .. amax, <Colors = [c1, c2, …]>, <attributes>)
plotfunc2d(f1, f2, ...) генерирует 2D график одномерных функций f1, f2 и т.д.
Мы строго рекомендуем читать введение в plotfunc2d в Разделе 2.1 (“2D Функциональные Графики”) документа графика.
Функции, которые будут построены, не должны содержать символьные параметры кроме переменной x и параметр анимации a. Точные численные значения, такие как PI, sqrt(2) и т.д. принят.
Анимации инициированы путем определения области значений a = amin .. amax для параметра a, который отличается от indedependent переменной x. Таким образом, в анимациях, оба x - область значений x = xmin .. xmax, а также область значений анимации a = amin .. amax должен быть задан. Смотрите Пример 2.
Проигнорированы недействительные значения функции. Смотрите Пример 3.
Функции с особенностями обработаны. Смотрите Пример 4 и Пример 5. Если неограниченные функции построены, вертикальная область значений просмотра отсекается, автоматически. Явную вертикальную область значений просмотра ymin .. ymax можно требовать через ViewingBoxYRange = `y_{min}` .. `y_{max}` или YRange = `y_{min}` .. `y_{max}`.
Разрывы и кусочные заданные функции обработаны. Смотрите Пример 6 и Пример 7.
Библиотека plot обеспечивает стандартный plot::Function2d, который позволяет создавать функциональный график как графический примитив, и комбинировать ее с другими графическими объектами.
Множество графических атрибутов может быть задано для точной настройки вывода графических данных. Такие атрибуты передаются как уравнения AttributeName = AttributeValue к команде plotfunc2d.
Разделите 2.3 (“Атрибуты для plotfunc2d, и plotfunc3d”) предоставляет обзор доступных атрибутов.
В частности, все атрибуты, принятые графическим примитивным plot::Function2d для функциональных графиков, приняты plotfunc2d. Эти атрибуты позволяют задавать mesh для численной оценки, ширина линии и т.д. Страница справки графика:: Function2d предоставляет краткий список.
Далее, все атрибуты, принятые plot::CoordinateSystem2d, приняты plotfunc2d. Эти атрибуты включают спецификацию поля просмотра, осей, их отметок деления и меток в виде галочки, координатный тип (такой как линейную по сравнению с логарифмическими графиками), линии сетки и т.д. Страница справки графика:: CoordinateSystem2d предоставляет краткий список.
Далее, все атрибуты, принятые plot::Scene2d, приняты plotfunc2d. Эти атрибуты включают спецификацию размещения графической сцены, цвет фона и т.д. Страница справки графика:: Scene2d предоставляет краткий список.
Далее, все атрибуты, принятые plot::Canvas, приняты plotfunc2d. Эти атрибуты включают спецификацию размера графики дальнейших параметров размещения и т.д. Страница справки графика:: Холст предоставляет краткий список.
Графический атрибут, такой как Mesh = 500 (определяющий номер точек mesh для численной оценки к 500) применяется ко всем функциям в вызове plotfunc2d(f1, f2, …). Если отдельные атрибуты являются соответствующими, используйте эквивалентный вызов
plot(plot::Function2d(f1, attr1), plot::Function2d(f2, attr2), …),
в котором атрибуты attr1, attr2 и т.д. может быть установлен отдельно для каждой функции.
Кроме немногих исключений, plotfunc2d использует стандартные значения по умолчанию для графических атрибутов (см. страницу справки plot::Function2d). Исключения:
Если больше чем одна функция построена, plotfunc2d автоматически создает легенду. Используйте явный LegendVisible = FALSE, чтобы подавить легенду.
AdaptiveMesh установлен в 2, т.е. plotfunc2d использует адаптивную функциональную оценку, если AdaptiveMesh = 0 не требуют в plotfunc2d.
Если область значений параметра, такая как x = `x_{min}` .. `x_{max}` передается plotfunc2d, имя, x используется в качестве заголовка для горизонтальной оси. Передайте атрибут XAxisTitle, если различная метка для горизонтальной оси желаема.
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность. Убедитесь, что DIGITS собирается в достаточно маленькое значение (такое как значение по умолчанию 10) избежать затрат на вычисление излишне точных данных о графике.
Следующая команда чертит синусоидальную функцию и косинусную функцию на интервале [-π, π]:
plotfunc2d(sin(x), cos(x), x = -PI .. PI):
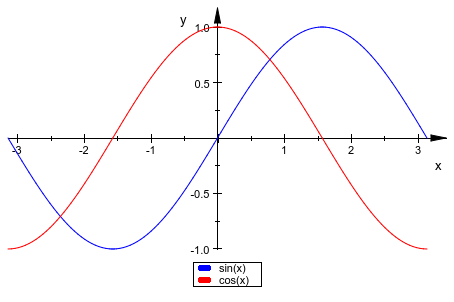
С атрибутом Scaling = Constrained, y - ось имеет ту же шкалу как x - ось:
plotfunc2d(sin(x), cos(x), x = -PI .. PI, Scaling = Constrained):
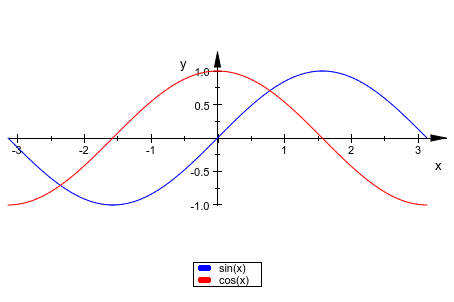
При создании анимации области значений для независимой переменной должен быть задан x. Дополнительная вторая область значений инициировала анимацию:
plotfunc2d(sin(x - a), cos(x + 2*a),
x = -PI .. PI, a = -PI .. PI)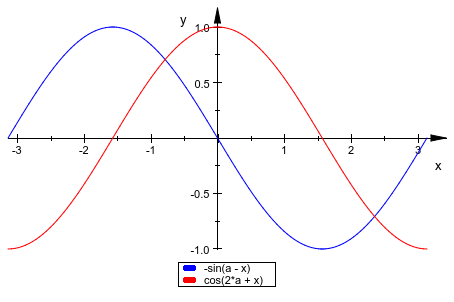
Только действительные значения функции построены:
plotfunc2d(sqrt(1 - x), sqrt(x), x = -2 .. 2):
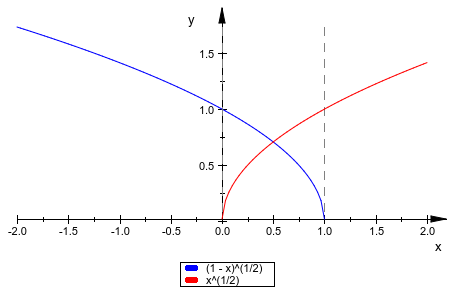
Следующие функции имеют особенности в заданном интервале:
plotfunc2d(x/(x^3 - 4*x), x = -5 .. 5):
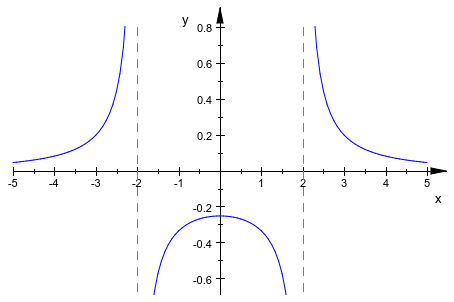
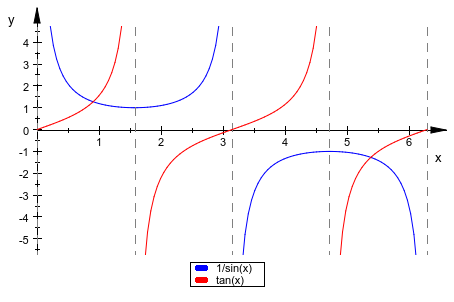
plotfunc2d(1/sin(x), tan(x), x = 0 .. 2*PI):
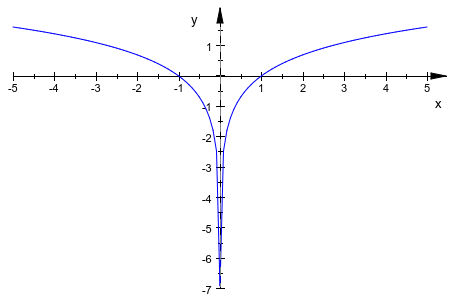
Обратите внимание на то, что автоматическое усечение может в некоторых случаях привести к неправильному впечатлению, такому как следующее изображение, где функция, кажется, сходится к приблизительно - 4.6 (но на самом деле переходит в - ∞ для небольших абсолютных значений x:
plotfunc2d(ln(abs(x)))
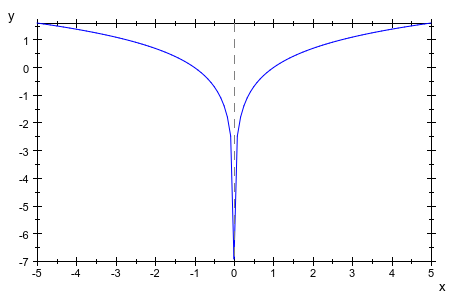
В этом случае асимптота, которая указывает на полюс, не замечена из-за оси:
plotfunc2d(ln(abs(x)), Axes=Boxed)
Мы задаем вертикальную область значений, которой ограничивается функциональный график:
plotfunc2d(tan(x), x = -3 .. 3, YRange = -10 .. 10):
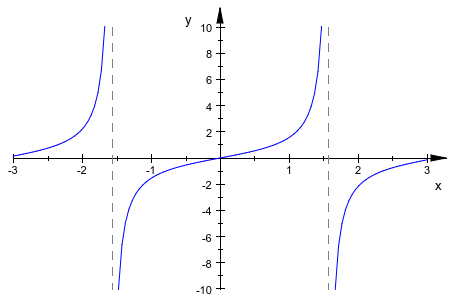
Следующая функция имеет разрыв скачка:
plotfunc2d((x^2 - x)/(2*abs(x - 1)), x = -3 .. 3,
YRange = -3 .. 3)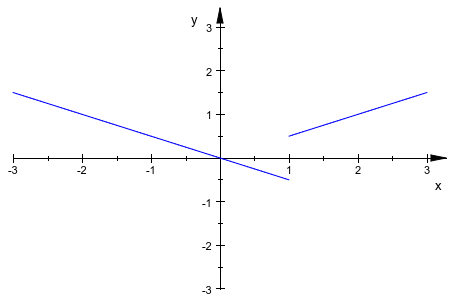
Обработаны кусочные заданные функции:
f := piecewise([x < 1, -x^2 + 1], [x >= 1, x]):
plotfunc2d(f(x), x = -3 .. 3, YRange = -3 .. 3,
GridVisible = TRUE, TicksDistance = 1)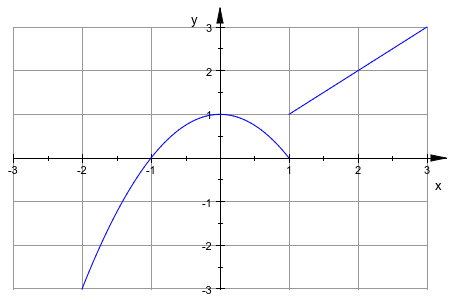
f := piecewise([x <= 0, x], [x > 0, 1/x]):
plotfunc2d(f(x), x = -3 .. 3, YRange = -3 .. 3,
GridVisible = TRUE, TicksDistance = 1)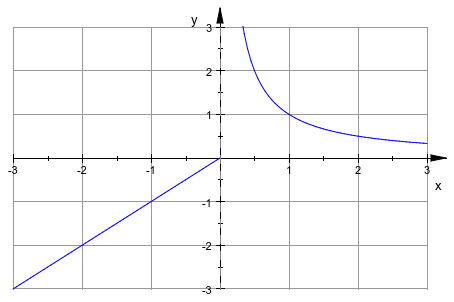
delete f:
Мы используем атрибут CoordinateType, чтобы создать логарифмический график:
plotfunc2d(exp(x/10) + exp(-x), x = -1 .. 10,
CoordinateType = LinLog)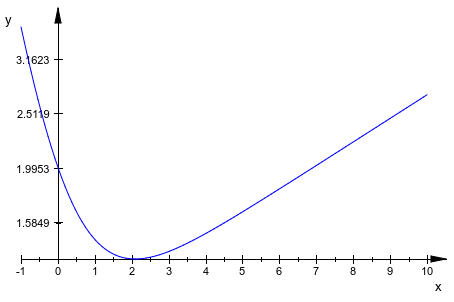
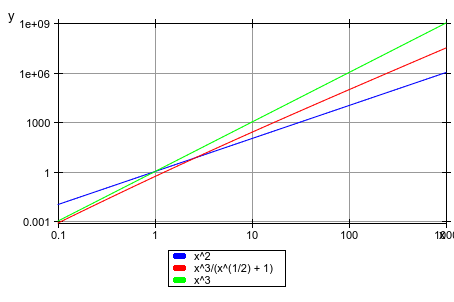
Мы демонстрируем различный далее графические атрибуты во вдвойне логарифмическом графике:
plotfunc2d(x^2, x^3/(1 + x^(1/2)), x^3,
x = 1/10 .. 10^3,
CoordinateType = LogLog,
Axes = Boxed,
DiscontinuitySearch = FALSE,
GridVisible = TRUE,
TicksNumber = None,
TicksAt = [[10^i $ i = -1 .. 3],
[10^i $ i in {-3, 0, 3, 6, 9}]
]):
|
Функции: арифметические выражения или |
|
Независимая переменная: идентификатор или индексируемый идентификатор. |
|
Область значений графика: |
|
Параметр анимации: идентификатор или индексируемый идентификатор. |
|
Область значений анимации: |
|
Цвета для |
|
Произвольное число графических атрибутов. Каждый атрибут дан уравнением формы |
Инструмент графики MuPAD® называется, чтобы представить графическую сцену. Объект null () возвращен в сеанс MuPAD.