6DOF Wind (Quaternion)

Реализуйте представление кватерниона шести уравнений степеней свободы движения относительно осей ветра

Библиотека

Уравнения Motion/6DOF

Описание

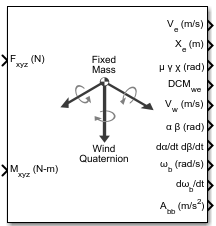
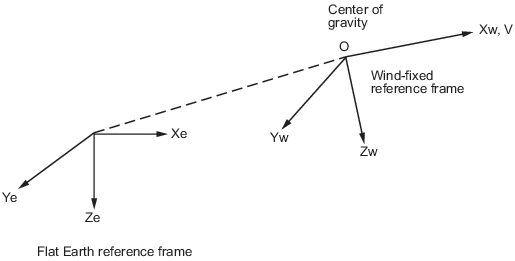
Блок 6DOF Wind (Quaternion) рассматривает вращение зафиксированной ветром координатной системы координат (_{Xw, Yw, Zw}) о плоской Наземной системе координат (_{Xe, Ye, Ze}). Источник зафиксированной ветром координатной системы координат является центром тяжести тела, и тело принято, чтобы быть твердым, предположение, которое избавляет от необходимости рассматривать силы, действующие между отдельными элементами массы. Плоская Наземная система координат рассматривается инерционной, превосходное приближение, которое позволяет силам из-за движения Земли относительно “фиксированных звезд” быть пропущенными.

Поступательное движение зафиксированной ветром координатной системы координат приведено ниже, где приложенные силы [_{Fx Fy Fz}] ^Tнаходятся в зафиксированной ветром системе координат и массе тела, m принят постоянный.

$\begin{array}{l} {\bar{F}}_{w} = [\begin{matrix} F_{x} \\ F_{y} \\ F_{z} \end{matrix}] = m ({\dot{\bar{V}}}_{w} + {\bar{ω}}_{w} \times {\bar{V}}_{w}) \\ A_{b e} = D C M_{w b} \frac{{\bar{F}}_{w}}{m} \\ {\bar{V}}_{w} = [\begin{matrix} V \\ 00 \end{matrix}], {\bar{ω}}_{w} = [\begin{matrix} p_{w} \\ q_{w} \\ r_{w} \end{matrix}] = D M C_{w b} [\begin{matrix} p_{b} - \dot{β} \sin α \\ q_{b} - \dot{α} \\ r_{b} + \dot{β} потому что α \end{matrix}], {\bar{ω}}_{b} = [\begin{matrix} p_{b} \\ q_{b} \\ r_{b} \end{matrix}] \\ A_{b b} = [\begin{matrix} {\dot{u}}_{b} \\ {\dot{v}}_{b} \\ {\dot{w}}_{b} \end{matrix}] = D C M_{w b} [\frac{{\bar{F}}_{w}}{m} - {\bar{ω}}_{w} \times {\bar{V}}_{w}] \end{array}$

Вращательные движущие силы зафиксированной телом системы координат приведены ниже, где прикладные моменты [L M N] ^T и тензор инерции, I относительно источника O. Тензор инерции I намного легче задать в зафиксированной телом системе координат.

$\begin{array}{l} {\bar{M}}_{b} = [\begin{matrix} L \\ M \\ N \end{matrix}] = I {\dot{\bar{ω}}}_{b} + {\bar{ω}}_{b} \times (I {\bar{ω}}_{b}) \\ I = [\begin{matrix} I_{x x} & - I_{x y} & - I_{x z} \\ - I_{y x} & I_{y y} & - I_{y z} \\ - I_{z x} & - I_{z y} & I_{z z} \end{matrix}] \end{array}$

Интегрирование скорости изменения вектора кватерниона приведено ниже.

$[\begin{matrix} {\dot{q}}_{0} \\ {\dot{q}}_{1} \\ {\dot{q}}_{2} \\ {\dot{q}}_{3} \end{matrix}] = - \frac{}{12} [\begin{matrix} 0 & p & q & r \\ - p & 0 & - r & q \\ - q & r & 0 & - p \\ - r & - q & p & 0 \end{matrix}] [\begin{matrix} q_{0} \\ q_{1} \\ q_{2} \\ q_{3} \end{matrix}]$

Параметры

Основной

Units

Задает модули ввода и вывода:

Модули	Силы	Момент	Ускорение	Скорость	Положение	Масса	Инерция
`Metric (MKS)`	Ньютон	Ньютон-метр	Метры в секунду придали квадратную форму	Метры в секунду	Метры	Килограмм	Килограммометр придал квадратную форму
`English (Velocity in ft/s)`	Фунт	Фунт ноги	Ноги в секунду придали квадратную форму	Ноги в секунду	Футы	Краткий заголовок	Отложите нога придала квадратную форму
`English (Velocity in kts)`	Фунт	Фунт ноги	Ноги в секунду придали квадратную форму	Узлы	Футы	Краткий заголовок	Отложите нога придала квадратную форму

Mass Type

Выберите тип массы, чтобы использовать:

`Fixed`	Масса является постоянной в течение симуляции.
`Simple Variable`	Масса и инерция варьируются линейно как функция массового уровня.
`Custom Variable`	Масса и изменения инерции настраиваемы.

Fixed выбор соответствует ранее описанным уравнениям движения.

Representation

Выберите представление использованию:

`Wind Angles`	Используйте углы ветра в рамках уравнений движения.
`Quaternion`	Используйте кватернионы в рамках уравнений движения.

Quaternion выбор соответствует ранее описанным уравнениям движения.

Initial position in inertial axes

Трехэлементный вектор для начального местоположения тела в плоской Наземной системе координат.

Initial airspeed, angle of attack, and sideslip angle

Трехэлементный вектор, содержащий начальную скорость полета, начальный угол нападения и начальный угол заноса.

Initial wind orientation

Трехэлементный вектор, содержащий начальные углы ветра [банк, курс полета, и направляющийся], в радианах.

Initial body rotation rates

Трехэлементный вектор для начальной буквы зафиксированные телом угловые уровни, в радианах в секунду.

Initial mass

Масса твердого тела.

Inertia matrix

3х3 матрица тензора инерции I, в зафиксированных телом осях.

Include inertial acceleration

Установите этот флажок, чтобы включить дополнительный выходной порт для ускорений в зафиксированных телом осях относительно инерционной системы координат. Вы обычно соединяете этот сигнал с акселерометром.

Атрибуты состояния

Присвойте уникальное имя каждому состоянию. Можно использовать имена состояния вместо путей к блоку во время линеаризации.

Чтобы присвоить имя к одному состоянию, введите уникальное имя между кавычками, например, 'velocity'.
Чтобы присвоить имена к нескольким состояниям, введите разграниченный запятой список, окруженный фигурными скобками, например, {'a', 'b', 'c'}. Каждое имя должно быть уникальным.
Если параметр пуст (' '), никакое присвоение имени не происходит.
Имена состояния применяются только к выбранному блоку параметром имени.
Количество состояний должно разделиться равномерно среди количества имен состояния.
Можно задать меньше имен, чем состояния, но вы не можете задать больше имен, чем состояния.
Например, можно задать два имени в системе с четырьмя состояниями. Имя применяется к первым двум состояниям и второму имени к последним двум состояниям.
Чтобы присвоить имена состояния с переменной в рабочей области MATLAB^®, введите переменную без кавычек. Переменная может быть вектором символов, массивом ячеек или структурой.

Position: e.g., {'Xe', 'Ye', 'Ze'}

Задайте имена состояния положения.