argАргумент (угол в полярных координатах) комплексного числа
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
arg(z) arg(x,y)
arg(z) возвращает аргумент комплексного числа z.
arg(x, y) возвращает аргумент комплексного числа с действительной частью x и мнимая часть y.
Эта функция также известна как atan2 на других математических языках.
Аргумент ненулевого комплексного числа z = x + i y = |z | e i ϕ является своим действительным углом в полярных координатах ϕ. arg(x,y) представляет основное значение![]() . Для x ≠ 0, y ≠ 0, этим дают
. Для x ≠ 0, y ≠ 0, этим дают
![]()
Ошибка происходит если arg вызван двумя аргументами и любым из аргументов xY недействительное численное значение. Символьные аргументы приняты, чтобы быть действительными.
С другой стороны, если arg вызван только одним аргументом x + I*y, это не принято тот x и y действительны.
Число с плавающей запятой возвращено, если один аргумент дан, который является числом с плавающей запятой; или если два аргумента даны, они оба числовые, и по крайней мере один из них является числом с плавающей запятой.
Если знак аргументов может быть определен, то результат выражается в терминах arctan. См. Пример 2. В противном случае, символьный вызов arg возвращен. Числовые факторы устраняются из первого аргумента. См. Пример 3.
Символьный вызов arg возвращенный имеет только один аргумент.
Вызов arg(0,0), или эквивалентно arg(0), возвращает 0.
Альтернативное представление![]() . См. Пример 4.
. См. Пример 4.
Когда названо аргументами с плавающей точкой, функция чувствительна к переменной окружения DIGITS который определяет числовую рабочую точность. Свойства идентификаторов учтены.
Мы демонстрируем некоторые вызовы с точными и символьными входными данными:
arg(2, 3), arg(x, 4), arg(4, y), arg(x, y), arg(10, y + PI)
![]()
Если arg вызван двумя аргументами, аргументы неявно приняты, чтобы быть действительными, который позволяет некоторые дополнительные упрощения по сравнению с вызовом только с одним аргументом:
arg(1, y), arg(1 + I*y)
![]()
arg(x, infinity), arg(-infinity, 3), arg(-infinity, -3)
![]()
Значения с плавающей точкой вычисляются для аргументов с плавающей точкой:
arg(2.0, 3), arg(2, 3.0), arg(10.0^100, 10.0^(-100))
![]()
arg реагирует на свойства набора идентификаторов через assume:
assume(x > 0): assume(y < 0): arg(x, y)
![]()
assume(x < 0): assume(y > 0): arg(x, y)
![]()
assume(x <> 0): arg(x, 3)
![]()
unassume(x), unassume(y):
Определенные упрощения могут произойти в неоцененных вызовах. В частности, числовые факторы устраняются из первого аргумента:
arg(3*x, 9*y), arg(-12*sqrt(2)*x, 12*y)
![]()
Используйте rewrite преобразовывать символьные вызовы arg к логарифмическому представлению:
rewrite(arg(x, y), ln)
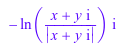
Системные функции, такие как float, limit, или series обработайте выражения, включающие arg:
limit(arg(x, x^2/(1+x)), x = infinity)
![]()
series(arg(x, x^2), x = 1, 4, Real)
![]()
| |
|
арифметические выражения, представляющие вещественные числа |
Арифметическое выражение.
xZ