plot::IntegralЧисловое приближение интеграла
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
plot::Integral(f, <n>, <IntMethod = m>, <a = amin .. amax>, options)
plot::Integral(f, IntMethod = m) визуализирует приближение интеграла функционального f использование числового квадратурного метода m. Суммы Римана, метод трапеций и правило Симпсона доступны.
plot::Integral(f, n, IntMethod = m) использование n подынтервалы, чтобы аппроксимировать интеграл.
Атрибут IntMethod определяет численный метод. Суммы Римана, метод трапеций или правило Симпсона доступны. Смотрите страницу справки IntMethod для получения дальнейшей информации. См. Пример 1.
plot::Integral не строит функциональный график подынтегрального выражения. Если подынтегральное выражение должно быть построено также f должен быть передан plot команда вместе с объектом приближения типа plot::Integral.
Если никакой квадратурный метод не задан IntMethod = m, plot::Integral только штрихует область между функциональным f и ось X.
Несколько plot::Integral объекты могут быть построены вместе, чтобы проиллюстрировать различие между различными квадратурными методами. Порядок объектов в plot команда определяет объект впереди.
График содержит информацию о предоставляющем текстового объекта о квадратурном методе, значении приближения, точном значении интеграла, квадратурной ошибки и количества узлов. Смотрите страницу справки атрибута ShowInfo для получения дальнейшей информации.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AffectViewingBox | влияние объектов на ViewingBox из сцены | TRUE |
AntiAliased | сглаженные линии и точки? | TRUE |
Color | основной цвет | RGB::PaleBlue |
Filled | заполненные или прозрачные области и поверхности | TRUE |
FillColor | цвет областей и поверхностей | RGB::PaleBlue |
FillPattern | тип заполнения области | Solid |
Frames | количество систем координат в анимации | 50 |
Function1 | первая штриховка разграничивания функции/кривой | |
HorizontalAlignment | выравнивание по горизонтали текстовых объектов w.r.t. их координаты | Left |
IntMethod | метод для интегрального приближения | Exact |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
LineColor | цвет линий | RGB::Black |
LineWidth | ширина линий | 0.35 |
LineColor2 | цвет линий | RGB::Grey |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LinesVisible | видимость линий | TRUE |
LineColorType | типы окраски линии | Flat |
LineColorFunction | функциональная окраска линии | |
Name | имя объекта графика (для браузера и легенды) | |
Nodes | количество подынтервалов или список x-значений для подынтервалов | [10 |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
PointSize | размер точек | 1.5 |
PointStyle | стиль презентации точек | FilledCircles |
PointsVisible | видимость точек mesh | FALSE |
ShowInfo | Информация об интегральном приближении | [2IntMethodинтеграл] |
TextFont | шрифт текстовых объектов | [" sans-serif ", 11 |
TextRotation | вращение 2D текста | 0 |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11 |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
VerticalAlignment | выравнивание по вертикали текстовых объектов w.r.t. их координаты | Bottom |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
Если один plot::Function2d объект дан, не задавая метод приближения, plot::Integral только штрихует область между функциональным графиком и осью X:
f := plot::Function2d(cos(x), x = -PI..PI): plot(plot::Integral(f), f)
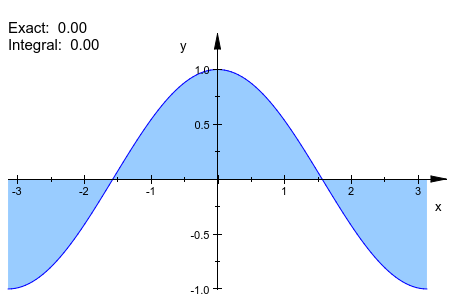
Обратите внимание на то, что plot::Integral требует объекта типа plot::Function2d, не только выражение function:
plot::Integral(sin(x))
Error: First argument must be a 'plot::Function2d' object. [plot::Integral::new]
Если метод приближения задан, числовое квадратурное значение, вычисленное этим методом, отображено:
plot(plot::Integral(f, IntMethod = RiemannLower))
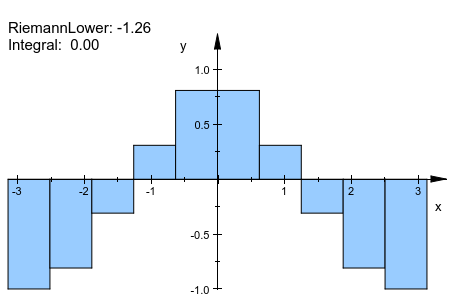
Номер квадратурных интервалов может быть определен путем передачи второго аргумента n или путем определения Nodes = n:
plot(plot::Integral(f, 20, IntMethod = RiemannLower))
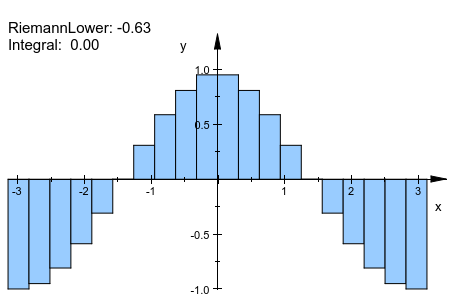
Чтобы видеть подынтегральное выражение в графике, функциональный объект должен быть передан вместе с объектом приближения. Порядок определяет, который объект впереди:
plot(plot::Integral(f, IntMethod = RiemannLower), f)
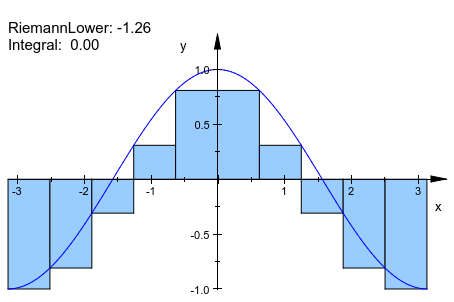
delete f:
Отображенная информация может быть сконфигурирована пользователем:
f := plot::Function2d(x^2, x = -5..5, Color = RGB::DarkGrey):
plot(plot::Integral(f, IntMethod = RiemannLower,
ShowInfo = [1, IntMethod = "Riemann lower sum",
Integral = "Exact value",
2, Error = "Difference"]), f)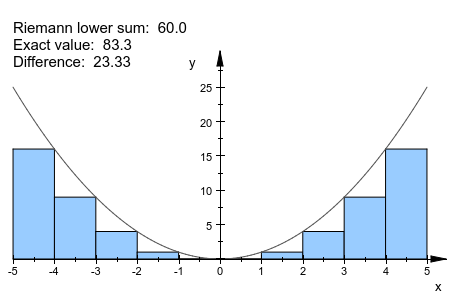
delete f:
Можно объединить несколько объектов приближения, например, ниже и верхняя сумма:
f := plot::Function2d(x^2, x = -5..5):
plot(plot::Integral(f, IntMethod = RiemannUpper,
Color = RGB::Blue),
plot::Integral(f, IntMethod = RiemannLower,
Color = RGB::LightYellow),
f)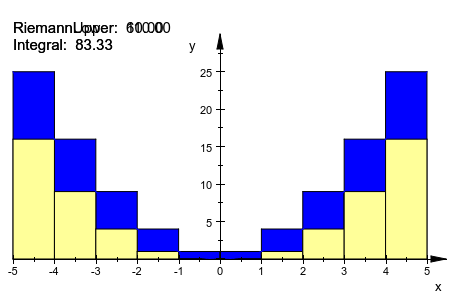
Автоматически помещенное информационное текстовое перекрытие. Откорректировать это, опция ShowInfo должен использоваться. В тексте верхней суммы вставляется одна дополнительная пустая линия. Кроме этого, оба объекта используют значение по умолчанию, поэтому нет потребности задать ShowInfo во втором объекте:
plot(plot::Integral(f, IntMethod = RiemannUpper,
ShowInfo = [IntMethod, "", Integral]),
plot::Integral(f, IntMethod = RiemannLower,
Color = RGB::LightYellow),
f)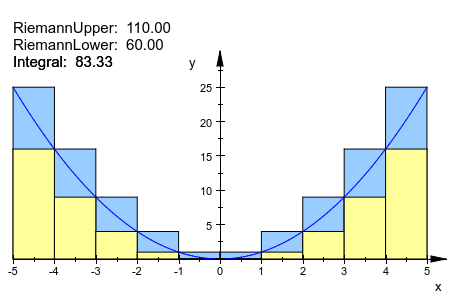
Информационный текст может быть расположен явным образом:
plot(plot::Integral(f, IntMethod = RiemannUpper,
ShowInfo = [IntMethod, Integral,
Position = [-5, -1]],
VerticalAlignment = Top),
plot::Integral(f, IntMethod = RiemannLower, Color = RGB::Yellow,
ShowInfo = [IntMethod,
Position = [0, -1]],
VerticalAlignment = Top),
f)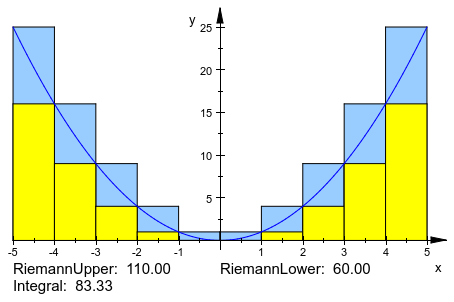
delete f:
plot::Integral может быть анимирован:
f := plot::Function2d(sin(a*x), x = 0..PI, a = 1..5): plot(plot::Integral(f, 50, IntMethod = RiemannMiddle), f)
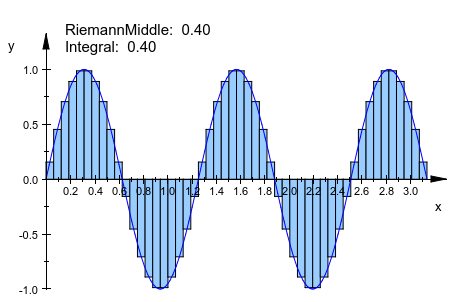
Увеличение числа узлов уменьшает квадратурную ошибку:
f := plot::Function2d(sin(x), x = 0..PI): plot(plot::Integral(f, N, N = 10..50, IntMethod = RiemannLower), f)
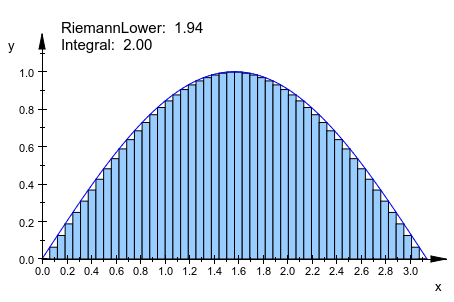
Функция и количество узлов могут быть анимированы одновременно:
f := plot::Function2d(sin(a*x), x = 0..PI, a = 1..5): plot(plot::Integral(f, N, N = 10..50, IntMethod = RiemannLower), f)
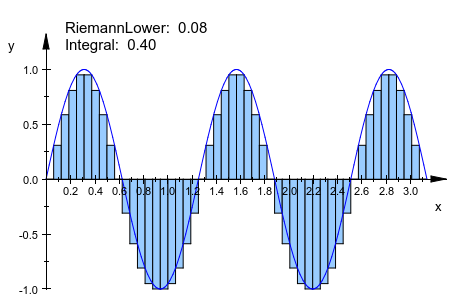
delete f:
|
Подынтегральное выражение: объект типа
|
|
Количество подынтервалов (положительное целое число) или список вещественных чисел, представляющих узлы переменной интегрирования.
|
|
Параметр анимации, заданный как |
|
Опция, заданная как Квадратурный метод; смотрите |