`plot`::`Matrixplot`

Объемная поверхностная диаграмма матричных данных

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

plot::Matrixplot(A, options)
plot::Matrixplot(A, x = x_min .. x_max, y = y_min .. y_max, <a = a_min .. a_max>, options)
plot::Matrixplot(row₁, row₂, …, options)
plot::Matrixplot(row₁, row₂, …, x = x_min .. x_max, y = y_min .. y_max, <a = a_min .. a_max>, options)
plot::Matrixplot([row₁, row₂, …], options)
plot::Matrixplot([row₁, row₂, …], x = x_min .. x_max, y = y_min .. y_max, <a = a_min .. a_max>, options)
plot::Matrixplot(s, <c₁, c₂, …>, options)
plot::Matrixplot(s, <c₁, c₂, …>, x = x_min .. x_max, y = y_min .. y_max, <a = a_min .. a_max>, options)
plot::Matrixplot(s, <[c₁, c₂, …]>, options)
plot::Matrixplot(s, <[c₁, c₂, …]>, x = x_min .. x_max, y = y_min .. y_max, <a = a_min .. a_max>, options)

Описание

plot::Matrixplot(A) визуализирует матричный A как 3D функциональный график путем интерполяции матричных значений как функции матричных индексов.

Matrixplot интерпретирует индексы матрицы как x и координаты y и соответствующая матричная запись как соответствующая координата z. Таким образом матрица рассматривается как дискретизированная функция в 2 переменных. Функциональный график отображен как 3D поверхность с помощью интерполяции между точками данных.

Если никакие области значений x = `x_{min}` .. `x_{max}`, y = `y_{min}` .. `y_{max}` заданы, матричная запись A[i, j] diplayed как 3D точка x = j, y = i, z = A[i, j] с целочисленными положениями i, j. Если диапазоны графика указаны, матричные индексы i, j используется, чтобы задать равноотстоящую mesh в области значений графика.

Атрибут InterpolationStyle позволяет задавать поверхность через линейную интерполяцию или интерполяцию кубическим сплайном точек данных: Выберите между InterpolationStyle = Linear или InterpolationStyle = Cubic. Значением по умолчанию является линейная интерполяция. С кубичной интерполяцией поверхность данных может быть сглажена путем определения номеров _{mx, my} из графика указывает между точками данных через атрибут Submesh = _{[mx, my]}. Числа _mx, _my должны быть (маленькие) неотрицательные целые числа.

С InterpolationStyle = Linear, символьные значения и комплексные числа приняты и проигнорированы, ведя к разрывам на поверхности. С InterpolationStyle = Cubic, символьные значения или комплексные числа приводят к ошибке. См. Пример 4.

По умолчанию точки данных представляются на поверхности. Используйте PointsVisible = FALSE заставить их исчезнуть.

Анимации инициированы путем указания диапазона a = `a_{min}` .. `a_{max}` для параметра a это отличается от переменных xY. Таким образом, в анимациях, оба области значений x = `x_{min}` .. `x_{max}`, y = `y_{min}` .. `y_{max}` а также анимация располагается a = `a_{min}` .. `a_{max}` должен быть задан.

Атрибуты

Атрибут	Цель	Значение по умолчанию
`AffectViewingBox`	влияние объектов на `ViewingBox` из сцены	`TRUE`
`Color`	основной цвет	`RGB::Red`
`Data`	(статистические) данные, чтобы построить
`Filled`	заполненные или прозрачные области и поверхности	`TRUE`
`FillColor`	цвет областей и поверхностей	`RGB::Red`
`FillColor2`	второй цвет областей и поверхностей для цветных смешений	`RGB::CornflowerBlue`
`FillColorType`	типы заполнения поверхности	`Dichromatic`
`FillColorFunction`	функциональная область / поверхностная окраска
`FillColorDirection`	направление цветовых переходов на поверхностях	[0, 0, 1]
`FillColorDirectionX`	x-компонент направления цветовых переходов на поверхностях	0
`FillColorDirectionY`	y-компонент направления цветовых переходов на поверхностях	0
`FillColorDirectionZ`	z-компонент направления цветовых переходов на поверхностях	1
`Frames`	количество систем координат в анимации	50
`InterpolationStyle`	интерполяция через линейные или кубические сплайны	`Linear`
`Legend`	делает запись легенды
`LegendText`	короткий объяснительный текст для легенды
`LegendEntry`	добавить этот объект в легенду?	`FALSE`
`LineColor`	цвет линий	`RGB::Black.[0.25]`
`LineWidth`	ширина линий	0.35
`LineColor2`	цвет линий	`RGB::DeepPink`
`LineStyle`	тело, подчеркнутые штриховой линией или пунктирные линии?	`Solid`
`LineColorType`	типы окраски линии	`Flat`
`LineColorFunction`	функциональная окраска линии
`LineColorDirection`	направление цветовых переходов на линиях	[0, 0, 1]
`LineColorDirectionX`	x-компонент направления цветовых переходов на линиях	0
`LineColorDirectionY`	y-компонент направления цветовых переходов на линиях	0
`LineColorDirectionZ`	z-компонент направления цветовых переходов на линиях	1
`Name`	имя объекта графика (для браузера и легенды)
`ParameterEnd`	закончите значение параметра анимации
`ParameterName`	имя параметра анимации
`ParameterBegin`	начальное значение параметра анимации
`ParameterRange`	область значений параметра анимации
`PointSize`	размер точек	1.5
`PointColor`	цвет точек	`RGB::MidnightBlue`
`PointStyle`	стиль презентации точек	`FilledCircles`
`PointsVisible`	видимость точек mesh	`TRUE`
`Shading`	сглаживайте цветное смешение поверхностей	`Smooth`
`Submesh`	плотность подmesh (дополнительные точки выборки)	[2, 2]
`TimeEnd`	время окончания анимации	10.0
`TimeBegin`	время начала анимации	0.0
`TimeRange`	оперативный промежуток анимации	0.0.. 10.0
`Title`	объектный заголовок
`TitleFont`	шрифт объектных заголовков	[`" sans-serif "`, 11]
`TitlePosition`	положение объектных заголовков
`TitleAlignment`	выравнивание по горизонтали заголовков w.r.t. их координаты	`Center`
`TitlePositionX`	положение объектных заголовков, x компонент
`TitlePositionY`	положение объектных заголовков, y компонент
`TitlePositionZ`	положение объектных заголовков, z компонент
`Visible`	видимость	`TRUE`
`VisibleAfter`	объект, видимый после этой временной стоимости
`VisibleBefore`	объект, видимый до этой временной стоимости
`VisibleFromTo`	объект, видимый в это время, располагается
`VisibleAfterEnd`	объект, видимый после его законченного времени анимации?	`TRUE`
`VisibleBeforeBegin`	объект, видимый перед его временем анимации, запускается?	`TRUE`
`XLinesVisible`	видимость линий параметра (x линии)	`TRUE`
`XMax`	окончательное значение параметра “x”
`XMin`	начальное значение параметра “x”
`XName`	имя параметра “x”
`XRange`	область значений параметра “x”
`XSubmesh`	плотность дополнительных точек выборки для параметра “x”	2
`YLinesVisible`	видимость линий параметра (y линии)	`TRUE`
`YMax`	окончательное значение параметра “y”
`YMin`	начальное значение параметра “y”
`YName`	имя параметра “y”
`YRange`	область значений параметра “y”
`YSubmesh`	плотность дополнительных точек выборки для параметра “y”	2

Примеры

Пример 1

Этот пример демонстрирует общий синтаксис вызова. Данные передаются по-разному с помощью списка строк, массива и матрицы, соответственно:

A := [[2, 1, 1],
      [3, 4, 3],
      [3, 5, 4],
      [2, 6, 5]]:
plot(plot::Matrixplot(A))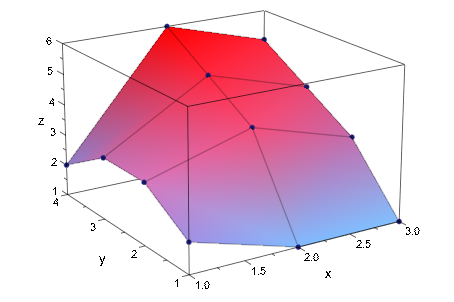

С InterpolationStyle = Cubic, матричные данные отображены на графике как кубическая поверхность сплайна:

A := array(1..4, 1..3, A):
plot(plot::Matrixplot(A, InterpolationStyle = Cubic)):

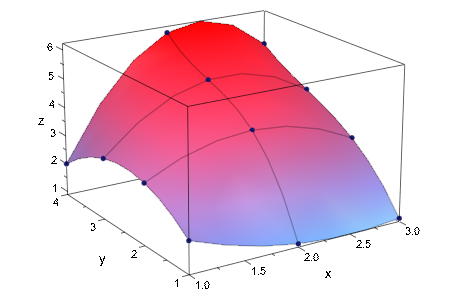
Поверхность сплайна может быть сглажена при помощи Submesh припишите, чтобы добавить дальнейшие точки оценки:

A := matrix(A):
plot(plot::Matrixplot(A, Submesh = [6, 6],
                      InterpolationStyle = Cubic)):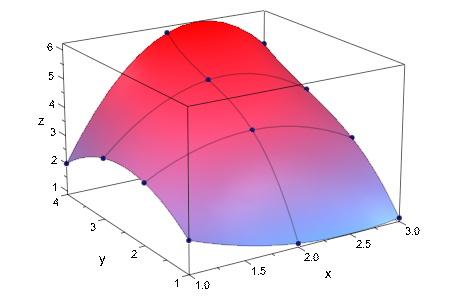

delete A:

Пример 2

Могут быть заданы различные атрибуты графика:

plot(plot::Matrixplot(
   [[-0.5,   0.5, 0.7, 0.5, -1  ], 
    [ 1.2, 1.3, 1.4, 1.4,  1  ],
    [ 1.4, 1.5, 1.6, 1.5,  1.2], 
    [ 0.6, 0.8, 1,   1,    1  ],
    [-0.7, 0.5, 0.5, 0,   -1  ]],
    PointsVisible = FALSE, 
    FillColor = RGB::Green,
    LineColor = RGB::Red))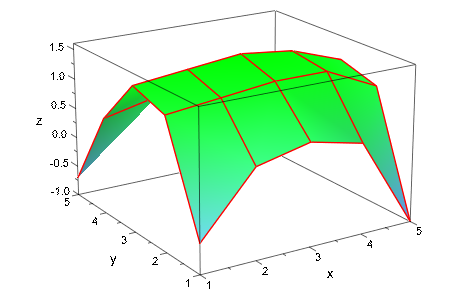

Пример 3

Выбирая соответствующие координатные области значений, мы помещаем два матричных графика рядом друг с другом:

plot(plot::Matrixplot(matrix::random(5, 5, frandom),
                      x = 0..1, y = 0..1, 
                      Color = RGB::Red),
     plot::Matrixplot(matrix::random(6, 6, frandom),
                      x = 2..3, y = 0..1,
                      Color = RGB::Green),
     Scaling = Constrained)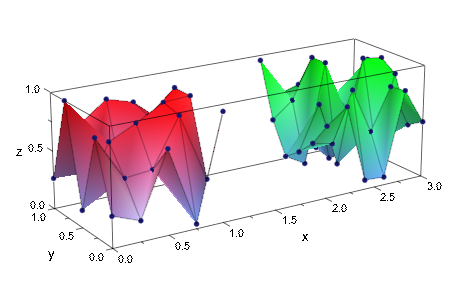

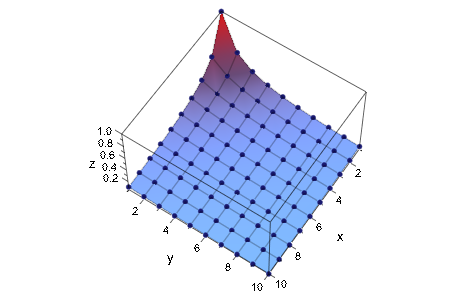
Пример 4

Мы строим Гильбертову матрицу:

A := linalg::hilbert(10):
plot(plot::Matrixplot(A), CameraDirection = [3, 2, 1])

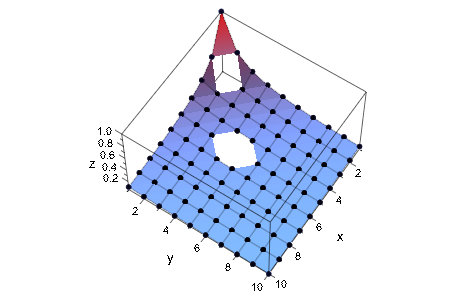
Некоторые записи заменяются значениями, которые не могут быть построены. Следовательно, график содержит отверстия:

A[2, 2] := NIL:
A[4, 5] := infinity:
A[5, 5] := x:
plot(plot::Matrixplot(A), CameraDirection = [3, 2, 1])

С InterpolationStyle = Cubic, ошибка повышена:

plot(plot::Matrixplot(A, InterpolationStyle = Cubic))

Error: Data contains nonreal numeric values. Use 'Style = Linear' to plot matrices containing such data. [plot::Matrixplot::doPlotStatic]
  Evaluating: plot

delete A:

Параметры

`A`	Матрица A категории `Cat::Matrix` или массив, содержащий действительные численные значения или выражения параметра анимации `a`. `A` эквивалентно атрибуту `Data`.
`_{row1, row2, …}`	Строки матрицы: каждая строка должна быть списком действительных численных значений или выражениями параметра анимации `a`. Все строки должны иметь ту же длину. `_row1`, `_row2`, … эквивалентен атрибуту `Data`.
`s`	Выборка данных доменного типа `stats::sample`. `s` эквивалентно атрибуту `Data`.
`_{c1, c2, …}`	Индексы столбца `s`: положительные целые числа. Эти индексы, если дали, указывают, что только заданные столбцы должны использоваться. Индексированные столбцы должны содержать действительные численные значения или выражения параметра анимации `a`, Если никакие столбцы не заданы, все столбцы `s` используются.
`x`	Имя первой координаты: идентификатор или индексируемый идентификатор. Это используется в качестве заголовка координатной оси в направлении x. `x` эквивалентно атрибуту `XName`.
`_{xmin .. xmax}`	Область значений первой координаты: `_xmin_xmax` должно быть числовое действительное значение или выражения параметра анимации a. `_xmin` `_xmax` эквивалентно атрибутам `XRangexmin` `xmax` .
`y`	Имя второй координаты: идентификатор или индексируемый идентификатор. Это используется в качестве заголовка координатной оси в направлении y. `y` эквивалентно атрибуту `YName`.
`_{ymin .. ymax}`	Область значений второй координаты: `_ymin_ymax` должно быть числовое действительное значение или выражения параметра анимации a. `_ymin` `_ymax` эквивалентно атрибутам `YRangeymin` `ymax` .
`a`	Параметр анимации, заданный как `a` `_{= amin..amax}`, где `_amin` начальное значение параметров и `_amax` итоговое значение параметров.

Документация

`plot`::`Matrixplot`

Синтаксис

Описание

Атрибуты

Примеры

Пример 1

Пример 2

Пример 3

Пример 4

Параметры

Смотрите также

Функции MuPAD

MuPAD графические примитивы

Документация Symbolic Math Toolbox

Поддержка