Настраиваемые переменные массовые 6DOF (углы Эйлера)

Реализация углового представления Эйлера уравнений движения пользовательской переменной массы с шестью степенями свободы

развернуть все на странице

Библиотека:
Аэрокосмический блок/Уравнения движения/ 6DOF

Описание

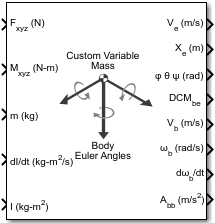
Блок 6DOF пользовательской переменной массы (Euler Angles) реализует представление угла Эйлера для уравнений шести степеней свободы движения пользовательской переменной массы. Рассматривается поворот неподвижной телом рамки координат (_Xb, _Yb, _Zb) относительно плоской системы координат Земли (_Xe, _Ye, _Ze). Дополнительные сведения об углах Эйлера см. в разделе Алгоритмы.

Ограничения

Блок предполагает, что приложенные силы действуют в центре тяжести тела.

Порты

Вход

развернуть все

`F_xyz` - Прикладываемые силы
трехэлементный вектор

Приложенные силы, заданные как трехэлементный вектор.

Типы данных: double

`M_xyz` - Прикладываемые моменты
трехэлементный вектор

Приложенные моменты, заданные как трехэлементный вектор.

Типы данных: double

`dm/dt` - Скорости изменения массы
трехэлементный вектор

Одна или несколько скоростей изменения массы (положительная при аккреции, отрицательная при абляции), заданная как трехэлементный вектор.

Зависимости

Чтобы включить этот порт, выберите Включить относительную скорость массового потока.

Типы данных: double

`m` - Масса
скаляр

Масса, заданная как скаляр.

Типы данных: double

`dI/dt` - Скорость изменения матрицы тензора инерции
Матрица 3 на 3

Скорость изменения матрицы тензора инерции, определяемая как матрица 3 на 3.

Типы данных: double

`I` - Матрица тензора инерции
Матрица 3 на 3

Матрица тензора инерции, заданная как матрица 3 на 3.

Типы данных: double

`V_re` - Относительные скорости
трехэлементный вектор

Одна или более относительных скоростей, при которых масса аккретируется или аблируется от тела в фиксированных по телу осях, определяемых как трехэлементный вектор.

Зависимости

Чтобы включить этот порт, выберите Включить относительную скорость массового потока.

Типы данных: double

Продукция

развернуть все

`V_e` - Скорость в плоской системе координат Земли
трехэлементный вектор

Скорость в плоской системе координат Земли, возвращаемая в виде трехэлементного вектора.

Типы данных: double

`X_e` - Положение в плоской системе координат Земли
трехэлементный вектор

Положение в плоской системе координат Земли, возвращаемое в виде трехэлементного вектора.

Типы данных: double

`φ θ ψ (rad)` - Углы поворота Эйлера
трехэлементный вектор

Углы поворота Эйлера [крен, тангаж, рыскание], возвращаемые в виде трёхэлементного вектора, в радианах.

Типы данных: double

`DCM_be` - Преобразование координат
Матрица 3 на 3

Преобразование координат из плоских осей Земли в фиксированные оси тела, возвращаемое в виде матрицы 3 на 3.

Типы данных: double

`V_b` - Скорость в неподвижной раме
трехэлементный вектор

Скорость в фиксированном теле кадра, возвращаемая как трехэлементный вектор.

Типы данных: double

`ω_b (rad/s)` - Угловые скорости в фиксированных осях корпуса
трехэлементный вектор

Угловые скорости в фиксированных по телу осях, возвращаемые как трёхэлементный вектор, в радианах в секунду.

Типы данных: double

`dω_b/dt` - Угловые ускорения
трехэлементный вектор

Угловые ускорения в фиксированных по телу осях, возвращаемые как трёхэлементный вектор, в радианах в секунду в квадрате.

Типы данных: double

`A_bb` - Ускорения в фиксированных по телу осях
трехэлементный вектор

Ускорения в фиксированных по телу осях относительно каркаса тела, возвращаемые в виде трехэлементного вектора.

Типы данных: double

`A_be` - Ускорения относительно инерциального каркаса
трехэлементный вектор

Ускорения в фиксированных по телу осях относительно инерциального каркаса (плоская Земля), возвращаемые как трёхэлементный вектор. Обычно этот сигнал подключается к акселерометру.

Зависимости

Этот порт появляется, только если установлен флажок Включить инерционное ускорение (Include inertial acceleration).

Типы данных: double

Параметры

развернуть все

Главный

`Units` - Блоки ввода и вывода
`Metric (MKS)` (по умолчанию) | `English (Velocity in ft/s)` | `English (Velocity in kts)`

Единицы ввода и вывода, указанные как Metric (MKS), English (Velocity in ft/s), или English (Velocity in kts).

Единицы	Силы	Момент	Ускорение	Скорость	Положение	Масса	Инерция
`Metric (MKS)`	Ньютон	Ньютон-метр	Метров в секунду в квадрате	Метров в секунду	Метры	Килограмм	Килограммовый метр в квадрате
`English (Velocity in ft/s)`	Фунт	Фут-фунт	Футов в секунду в квадрате	Футов в секунду	Ноги	Слизняк	Слизистая ножка в квадрате
`English (Velocity in kts)`	Фунт	Фут-фунт	Футов в секунду в квадрате	Узлы	Ноги	Слизняк	Слизистая ножка в квадрате

Программное использование

Параметр блока: units

Текст: символьный вектор

Значения: Metric (MKS) | English (Velocity in ft/s) | English (Velocity in kts)

По умолчанию: Metric (MKS)

`Mass type` - Тип массы
`Custom Variable` (по умолчанию) | `Simple Variable` | `Fixed`

Тип массы, указанный в следующей таблице.

Тип массы	Описание	По умолчанию для
`Fixed`	Масса постоянна на протяжении всего моделирования.	6DOF (Эйлеровы углы) 6DOF (кватернион) 6DOF Ветер (углы ветра) 6DOF Ветер (кватернион) 6DOF ECEF (кватернион)
`Simple Variable`	Масса и инерция изменяются линейно в зависимости от массового расхода.	Простые переменные массовые 6DOF (углы Эйлера) Простая переменная массовая 6DOF (кватернион) Простая переменная масса 6DOF ветер (углы ветра) Простая переменная масса 6DOF ветер (кватернион) Простая переменная масса 6DOF ECEF (кватернион)
`Custom Variable`	Вариации массы и инерции настраиваются.	Настраиваемые переменные массовые 6DOF (углы Эйлера) Настраиваемые переменные массовые 6DOF (кватернион) Пользовательская переменная масса 6DOF ветер (углы ветра) Пользовательская переменная масса 6DOF Ветер (кватернион) Настраиваемая переменная масса 6DOF ECEF (кватернион)

Custom Variable выбор соответствует ранее описанным уравнениям движения.

Программное использование

Параметр блока: mtype

Текст: символьный вектор

Значения: Fixed | Simple Variable | Custom Variable

По умолчанию: 'Custom Variable'

`Representation` - Уравнения представления движения
`Euler Angles` (по умолчанию) | `Quaternion`

Уравнения представления движения, указанные в следующей таблице.

Представление	Описание
`Euler Angles`	Используйте углы Эйлера в уравнениях движения.
`Quaternion`	Используйте кватернионы в уравнениях движения.

Quaternion выбор соответствует уравнениям движения в алгоритмах.

Программное использование

Параметр блока: rep

Текст: символьный вектор

Значения: Euler Angles | Quaternion

По умолчанию: 'Euler Angles'

`Initial position in inertial axes [Xe,Ye,Ze]` - Положение по инерционным осям
`[0 0 0]` (по умолчанию) | трехэлементный вектор

Начальное расположение тела в плоской системе координат Земли, определяемое как трехэлементный вектор.

Программное использование

Параметр блока: xme_0

Текст: символьный вектор

Значения: '[0 0 0]' | трехэлементный вектор

По умолчанию: '[0 0 0]'

`Initial velocity in body axes [U,v,w]` - Скорость в осях корпуса
`[0 0 0]` (по умолчанию) | трехэлементный вектор

Начальная скорость в осях тела, заданная как трехэлементный вектор, в фиксированном телом координатном кадре.

Программное использование

Параметр блока: Vm_0

Текст: символьный вектор

Значения: '[0 0 0]' | трехэлементный вектор

По умолчанию: '[0 0 0]'

`Initial Euler orientation [roll, pitch, yaw]` - Начальная ориентация Эйлера
`[0 0 0]` (по умолчанию) | трехэлементный вектор

Начальные углы ориентации Эйлера [крен, тангаж, рыскание], заданные как трехэлементный вектор, в радианах. Углы поворота Эйлера - это углы между системой координат корпуса и системой координат «север-восток-вниз» (NED).

Программное использование

Параметр блока: eul_0

Текст: символьный вектор

Значения: '[0 0 0]' | трехэлементный вектор

По умолчанию: '[0 0 0]'

`Initial body rotation rates [p,q,r]` - Начальное вращение тела
`[0 0 0]` (по умолчанию) | трехэлементный вектор

Начальные угловые скорости тела относительно кадра NED, определенные как трехэлементный вектор, в радианах в секунду.

Программное использование

Параметр блока: pm_0

Текст: символьный вектор

Значения: '[0 0 0]' | трехэлементный вектор

По умолчанию: '[0 0 0]'

`Include mass flow relative velocity` - Порт относительной скорости массового потока
`off` (по умолчанию) | `on`

Установите этот флажок, чтобы добавить порт относительной скорости массового потока. Это относительная скорость, с которой происходит аккреция или абляция массы.

Программное использование

Параметр блока: vre_flag

Текст: символьный вектор

Значения: off | on

По умолчанию: off

`Include inertial acceleration` - Включить инерционный порт ускорения
`off` (по умолчанию) | `on`

Установите этот флажок, чтобы добавить инерционный порт ускорения.

Зависимости

Для активизации порта _Abe выберите этот параметр.

Программное использование

Параметр блока: abi_flag

Текст: символьный вектор

Значения: 'off' | 'on'

По умолчанию: off

Атрибуты состояния

Присвойте каждому состоянию уникальное имя. Во время линеаризации вместо контуров блоков можно использовать имена состояний.

Чтобы назначить имя одному состоянию, введите уникальное имя между кавычками, например: 'velocity'.
Чтобы назначить имена нескольким состояниям, введите разделенный запятыми список, окруженный фигурными скобками, например: {'a', 'b', 'c'}. Каждое имя должно быть уникальным.
Если параметр пуст (' '), имя не назначено.
Имена состояний применяются только к выбранному блоку с параметром name.
Число состояний должно равномерно делиться между числом имен состояний.
Можно указать меньше имен, чем состояний, но нельзя указать больше имен, чем состояний.
Например, можно указать два имени в системе с четырьмя состояниями. Первое имя относится к первым двум состояниям, а второе - к последним двум состояниям.
Чтобы назначить имена состояний переменной в рабочей области MATLAB ®, введите переменную без кавычек. Переменная может быть символьным вектором, массивом ячеек или структурой.

`Position: e.g., {'Xe', 'Ye', 'Ze'}` - Наименование состояния позиции
`''` (по умолчанию) | разделенный запятыми список, окруженный фигурными скобками

Имена состояний позиций, заданные как разделенный запятыми список, окруженный фигурными скобками.

Программное использование

Параметр блока: xme_statename

Текст: символьный вектор

Значения: '' | разделенный запятыми список, окруженный фигурными скобками

По умолчанию: ''

`Velocity: e.g., {'U', 'v', 'w'}` - Название состояния скорости
`''` (по умолчанию) | разделенный запятыми список, окруженный фигурными скобками

Имена состояний скорости, указанные как разделенный запятыми список, окруженный фигурными скобками.

Программное использование

Параметр блока: Vm_statename

Текст: символьный вектор

Значения: '' | разделенный запятыми список, окруженный фигурными скобками

По умолчанию: ''

`Euler rotation angles: e.g., {'phi', 'theta', 'psi'}` - Имя состояния вращения Эйлера
`''` (по умолчанию) | разделенный запятыми список, окруженный фигурными скобками

Имена состояний угла поворота Эйлера, заданные как разделенный запятыми список, окруженный фигурными скобками.

Программное использование

Параметр блока: eul_statename

Текст: символьный вектор

Значения: '' | разделенный запятыми список, окруженный фигурными скобками

По умолчанию: ''

`Body rotation rates: e.g., {'p', 'q', 'r'}` - Имена состояний вращения тела
`''` (по умолчанию) | разделенный запятыми список, окруженный фигурными скобками

Имена состояний частоты вращения тела, указанный список разделенных запятыми фигурных скобок.

Программное использование

Параметр блока: pm_statename

Текст: символьный вектор

Значения: '' | разделенный запятыми список, окруженный фигурными скобками

По умолчанию: ''

Алгоритмы

Начало координат фиксированного тела - это центр тяжести тела. Тело предполагается жестким, что исключает необходимость учитывать силы, действующие между отдельными элементами массы. Плоская система отсчёта Земли считается инерционной, превосходной аппроксимацией, позволяющей пренебречь силами, обусловленными движением Земли относительно «неподвижных звёзд».

Поступательное движение неподвижного в теле кадра координат приведено ниже, где приложенные силы [_Fx _Fy _Fz] T находятся в неподвижном в теле кадре. Vreb - относительная скорость в осях тела, при которой массовый поток $\overset{}{(}$ m˙) выбрасывается или добавляется к фиксированным в теле осям.

$\begin{array}{l} {\overset{}{F}}_{_} b \begin{matrix} _{=} \\ _{[} \\ _{} \end{matrix} FxFyFz {\overset{=}{\overset{}{]}}}_{} m \overset{(}{} {\overset{}{}}_{} \overset{}{} \overset{}{} V¯˙b+ω¯×V¯b)_{} \\ _{} \frac{{\overset{}{}}_{} \overset{}{} {\overset{}{}}_{_{}}}{} \\ _{} \begin{matrix} {\overset{}{}}_{} \\ {\overset{}{}}_{} \\ {\overset{}{}}_{} \end{matrix} \frac{{\overset{}{}}_{} \overset{}{} {\overset{}{}}_{_{}}}{} \overset{}{} {\overset{}{}}_{} \\ {\overset{}{}}_{} \begin{matrix} _{} \\ _{} \\ _{} \end{matrix} \overset{}{} \begin{matrix} +m˙V¯rebAbe=F¯b−m˙V¯rebmAbb=[u˙bv˙bw˙b]=F¯b−m˙V¯rebm−ω¯×V¯bV¯b=[ubvbwb \\ ] \end{matrix}, \end{array}$ λ = [pqr]

Динамика вращения неподвижного корпуса представлена ниже, где прикладываемые моменты равны [L M N] T, а тензор инерции I относительно начала координат О .

$\begin{array}{l} {\overset{}{}}_{} \begin{matrix} \end{matrix} \overset{}{\overset{}{}} \overset{}{} M¯B=[LMN]=Iω¯˙+ω¯\times (\overset{Iλ)}{} \overset{}{} \overset{}{} \\ \begin{matrix} _{} & _{} & _{} \\ _{} & _{} & _{} \\ _{} & _{} & _{} \end{matrix} \\ \overset{}{} \begin{matrix} {\overset{}{}}_{} & {\overset{}{}}_{} & {\overset{}{}}_{} \\ {\overset{}{}}_{} & {\overset{}{}}_{} & {\overset{}{}}_{} \\ {\overset{}{}}_{} & {\overset{}{}}_{} & {\overset{}{}}_{} \end{matrix} \end{array}$ +I˙ω¯I=[Ixx−Ixy−Ixz−IyxIyy−Iyz−Izx−IzyIzz]I˙=[I˙xx−I˙xy−I˙xz−I˙yxI˙yy−I˙yz−I˙zx−I˙zyI˙zz]

Зависимость между фиксированным телом вектором угловой скорости, [p q r] T, и скоростью изменения углов Эйлера, ${\overset{}{[} \overset{}{} \overset{}{}}^{}$ ϕ˙θ˙ψ˙]T, может быть определена путем разрешения скоростей Эйлера в фиксированный телом кадр координат .

$[\begin{matrix} \end{matrix} \begin{matrix} \overset{}{} \end{matrix} \begin{matrix} pqr]=[ϕ˙00]+[1000cosϕsinϕ0−sinϕcosϕ \end{matrix}] \begin{matrix} [ \\ \overset{}{} \end{matrix} \begin{matrix} \end{matrix} 0θ˙0]+[1000cosϕsinϕ0-sinϕcosϕ] \begin{matrix} [ & cosun0 − \end{matrix} \begin{matrix} sinü 010sinstart0cosstart \\ \overset{}{]} \end{matrix} [^{} \begin{matrix} \overset{}{} \\ \overset{}{} \\ \overset{}{} \end{matrix}$ 00ψ˙]=J−1[ϕ˙θ˙ψ˙]

Затем инвертирование J дает требуемое соотношение для определения вектора скорости Эйлера.

$\begin{matrix} \overset{}{} \\ \overset{}{} \\ \overset{}{} \end{matrix} [ϕ˙θ˙ψ˙] =J \begin{matrix} \end{matrix} [pqr] = [\begin{matrix} 1 & (sinϕtanθ) \\ (cosϕtanθ) \\ \frac{}{} & \frac{}{} \end{matrix} \begin{matrix} 0cosϕ−sinϕ0sinϕcosθcosϕcosθ \\ ] \end{matrix}$ [pqr]

Дополнительные сведения о аэрокосмических системах координат см. в разделе Сведения об аэрокосмических системах координат.

Ссылки

[1] Стивенс, Брайан и Фрэнк Льюис. Управление и моделирование летательных аппаратов, 2-й ред. Хобокен, Нью-Джерси: John Wiley & Sons, 2003.

[2] Зипфель, Питер Х. Моделирование и моделирование динамики аэрокосмических аппаратов. 2-я ред. Рестон, VA: AIAA Education Series, 2007.

Расширенные возможности

Создание кода C/C + +
Создайте код C и C++ с помощью Simulink ® Coder™

См. также

Темы

Сведения об аэрокосмических системах координат

Представлен в R2006a

Документация

Настраиваемые переменные массовые 6DOF (углы Эйлера)

Описание

Ограничения

Порты

Вход

Fxyz - Прикладываемые силы трехэлементный вектор

Mxyz - Прикладываемые моменты трехэлементный вектор

dm/dt - Скорости изменения массы трехэлементный вектор

Зависимости

m - Масса скаляр

dI/dt - Скорость изменения матрицы тензора инерции Матрица 3 на 3

I - Матрица тензора инерции Матрица 3 на 3

Vre - Относительные скорости трехэлементный вектор

Зависимости

Продукция

Ve - Скорость в плоской системе координат Земли трехэлементный вектор

Xe - Положение в плоской системе координат Земли трехэлементный вектор

φ θ ψ (rad) - Углы поворота Эйлера трехэлементный вектор

DCMbe - Преобразование координат Матрица 3 на 3

Vb - Скорость в неподвижной раме трехэлементный вектор

ωb (rad/s) - Угловые скорости в фиксированных осях корпуса трехэлементный вектор

dωb/dt - Угловые ускорения трехэлементный вектор

Abb - Ускорения в фиксированных по телу осях трехэлементный вектор

Abe - Ускорения относительно инерциального каркаса трехэлементный вектор

Зависимости

Параметры

Главный

Units - Блоки ввода и вывода Metric (MKS) (по умолчанию) | English (Velocity in ft/s) | English (Velocity in kts)

Программное использование

Mass type - Тип массы Custom Variable (по умолчанию) | Simple Variable | Fixed

Программное использование

Representation - Уравнения представления движения Euler Angles (по умолчанию) | Quaternion

Программное использование

Initial position in inertial axes [Xe,Ye,Ze] - Положение по инерционным осям [0 0 0] (по умолчанию) | трехэлементный вектор

Программное использование

Initial velocity in body axes [U,v,w] - Скорость в осях корпуса [0 0 0] (по умолчанию) | трехэлементный вектор

Программное использование

Initial Euler orientation [roll, pitch, yaw] - Начальная ориентация Эйлера [0 0 0] (по умолчанию) | трехэлементный вектор

Программное использование

Initial body rotation rates [p,q,r] - Начальное вращение тела [0 0 0] (по умолчанию) | трехэлементный вектор

Программное использование

Include mass flow relative velocity - Порт относительной скорости массового потока off (по умолчанию) | on

Программное использование

Include inertial acceleration - Включить инерционный порт ускорения off (по умолчанию) | on

Зависимости

Программное использование

Атрибуты состояния

Position: e.g., {'Xe', 'Ye', 'Ze'} - Наименование состояния позиции '' (по умолчанию) | разделенный запятыми список, окруженный фигурными скобками

Программное использование

Velocity: e.g., {'U', 'v', 'w'} - Название состояния скорости '' (по умолчанию) | разделенный запятыми список, окруженный фигурными скобками

Программное использование

Euler rotation angles: e.g., {'phi', 'theta', 'psi'} - Имя состояния вращения Эйлера '' (по умолчанию) | разделенный запятыми список, окруженный фигурными скобками

Программное использование

Body rotation rates: e.g., {'p', 'q', 'r'} - Имена состояний вращения тела '' (по умолчанию) | разделенный запятыми список, окруженный фигурными скобками

Программное использование

Алгоритмы

Ссылки

Расширенные возможности

Создание кода C/C + + Создайте код C и C++ с помощью Simulink ® Coder™

См. также

Темы

Документация по аэрокосмическим блокам

Поддержка

`F_xyz` - Прикладываемые силы
трехэлементный вектор

`M_xyz` - Прикладываемые моменты
трехэлементный вектор

`dm/dt` - Скорости изменения массы
трехэлементный вектор

`m` - Масса
скаляр

`dI/dt` - Скорость изменения матрицы тензора инерции
Матрица 3 на 3

`I` - Матрица тензора инерции
Матрица 3 на 3

`V_re` - Относительные скорости
трехэлементный вектор

`V_e` - Скорость в плоской системе координат Земли
трехэлементный вектор

`X_e` - Положение в плоской системе координат Земли
трехэлементный вектор

`φ θ ψ (rad)` - Углы поворота Эйлера
трехэлементный вектор

`DCM_be` - Преобразование координат
Матрица 3 на 3

`V_b` - Скорость в неподвижной раме
трехэлементный вектор

`ω_b (rad/s)` - Угловые скорости в фиксированных осях корпуса
трехэлементный вектор

`dω_b/dt` - Угловые ускорения
трехэлементный вектор

`A_bb` - Ускорения в фиксированных по телу осях
трехэлементный вектор

`A_be` - Ускорения относительно инерциального каркаса
трехэлементный вектор

`Units` - Блоки ввода и вывода
`Metric (MKS)` (по умолчанию) | `English (Velocity in ft/s)` | `English (Velocity in kts)`

`Mass type` - Тип массы
`Custom Variable` (по умолчанию) | `Simple Variable` | `Fixed`

`Representation` - Уравнения представления движения
`Euler Angles` (по умолчанию) | `Quaternion`

`Initial position in inertial axes [Xe,Ye,Ze]` - Положение по инерционным осям
`[0 0 0]` (по умолчанию) | трехэлементный вектор

`Initial velocity in body axes [U,v,w]` - Скорость в осях корпуса
`[0 0 0]` (по умолчанию) | трехэлементный вектор

`Initial Euler orientation [roll, pitch, yaw]` - Начальная ориентация Эйлера
`[0 0 0]` (по умолчанию) | трехэлементный вектор

`Initial body rotation rates [p,q,r]` - Начальное вращение тела
`[0 0 0]` (по умолчанию) | трехэлементный вектор

`Include mass flow relative velocity` - Порт относительной скорости массового потока
`off` (по умолчанию) | `on`

`Include inertial acceleration` - Включить инерционный порт ускорения
`off` (по умолчанию) | `on`

`Position: e.g., {'Xe', 'Ye', 'Ze'}` - Наименование состояния позиции
`''` (по умолчанию) | разделенный запятыми список, окруженный фигурными скобками

`Velocity: e.g., {'U', 'v', 'w'}` - Название состояния скорости
`''` (по умолчанию) | разделенный запятыми список, окруженный фигурными скобками

`Euler rotation angles: e.g., {'phi', 'theta', 'psi'}` - Имя состояния вращения Эйлера
`''` (по умолчанию) | разделенный запятыми список, окруженный фигурными скобками

`Body rotation rates: e.g., {'p', 'q', 'r'}` - Имена состояний вращения тела
`''` (по умолчанию) | разделенный запятыми список, окруженный фигурными скобками

Создание кода C/C + +
Создайте код C и C++ с помощью Simulink ® Coder™