Сформировать линейно-квадратично-гауссовый (LQG) регулятор
rlqg = lqgreg(kest,k)
rlqg = lqgreg(kest,k,controls)
rlqg = lqgreg(kest,k) возвращает регулятор LQG rlqg (модель «государство-пространство») с помощью оценщика Калмана kest и матрица усиления с обратной связью о состоянии k. Одна и та же функция обрабатывает как непрерывные, так и дискретные случаи времени. Использование согласованных инструментов для проектирования kest и k:
Непрерывный регулятор для установки непрерывного действия: использование lqr или lqry и kalman
Дискретный регулятор для дискретной установки: использование dlqr или lqry и kalman
Дискретный регулятор для установки непрерывного действия: использование lqrd и kalmd
В дискретное время, lqgreg производит регулятор
[n 'n ] когдаkest является «текущим» оценщиком Калмана
n 'n − 1], когдаkest является «задержанным» оценщиком Калмана
Для получения дополнительной информации об оценщиках Kalman см. kalman справочная страница.
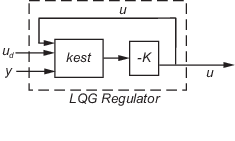
rlqg = lqgreg(kest,k,controls) обрабатывает оценщики, которые имеют доступ к дополнительным детерминированным известным установкам. Вектор индекса controls затем определяет, какие входы оценщика являются управляющими u, и результирующий регулятор LQG rlqg имеет ud и y в качестве входных данных (см. следующий рисунок).
Примечание
Всегда используйте положительную обратную связь для подключения регулятора LQG к установке.
См. пример LQG Regulation: Rolling Still Case Study.
lqgreg образует линейно-квадратично-гауссовый (LQG) регулятор, соединяя оценщик Калмана, сконструированный с kalman и оптимальное усиление обратной связи состояния, разработанное с помощью lqr, dlqr, или lqry. Регулятор LQG сводит к минимуму некоторую квадратичную функцию затрат, которая влияет на эффективность регулирования и усилия по контролю. Этот регулятор является динамическим и основан на шумных выходных измерениях для формирования команд регулирования.
В непрерывном режиме регулятор LQG формирует команды
Kx ^
где ^ - оценка состояния Калмана. Уравнения состояния-пространства регулятора:
Lyu = − Kx ^
где y - вектор измерений выхода установки (см. kalman для фона и обозначения). На следующей диаграмме показан динамический регулятор по отношению к установке.
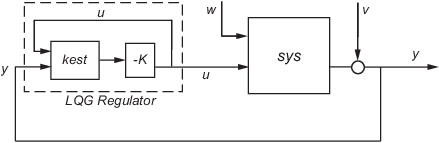
За дискретное время можно сформировать регулятор LQG, используя либо оценку отложенного состояния − 1] из x [n], основанную на измерениях до y [n-1], либо текущего состояния
n 'n − 1]
всегда четко определен, текущий регулятор
[n 'n]
является причинно-следственным только тогда, когда I-KMD является обратимым (см. kalman для обозначения). Кроме того, практические реализации регулятора тока должны обеспечивать время обработки, необходимое для вычисления u [n] после того, как измерения y [n] станут доступными (это равно временной задержке в контуре обратной связи).
Для установки дискретного времени с уравнениями:
[n] + v [n] {Измерения}
подключение «текущего» оценщика Калмана к коэффициенту усиления LQR является оптимальным только тогда, когда ′) = 0 и y [n] не зависит от w [n] (H = 0). Если эти условия не выполняются, вычислите оптимальный контроллер LQG с помощьюlqg.