Линейно-квадратично-интегральное управление
[K,S,e] = lqi(SYS,Q,R,N)
lqi вычисляет оптимальный закон управления с обратной связью для цикла слежения, показанного на следующем рисунке.
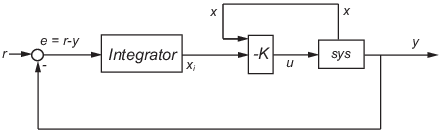
Для завода sys с уравнениями состояния-пространства (или их дискретным аналогом):
Cx + Du
контроль состояния с обратной связью имеет вид
; xi]
где xi - выход интегратора. Этот закон управления гарантирует, что выходной сигнал y отслеживает ссылочную команду r. Для систем MIMO количество интеграторов равно размеру выходного сигнала y.
[K,S,e] = lqi(SYS,Q,R,N) вычисляет матрицу оптимального усиления K, учитывая модель состояния-пространства SYS для завода и матриц взвешивания Q, R, N. Закон управления u = -Kz = -K [x; xi] минимизирует следующие функции затрат (для r = 0)
=∫0∞{zTQz+uTRu+2zTNu}dt в течение непрерывного времени
=∑n=0∞{zTQz+uTRu+2zTNu} для дискретного времени
В дискретное время, lqi вычисляет выход интегратора xi по прямой формуле Эйлера
[n] − y [n])
где Ts - время выборки SYS.
При пропуске матрицы N, N имеет значение 0. lqi также возвращает решение S связанного алгебраического уравнения Риккати и собственных значений замкнутого цикла e.
Для следующей государственно-космической системы с установкой с усиленным интегратором:
Caz + Dau
Данные проблемы должны удовлетворять следующим требованиям:
Пара (Aa, Ba) является стабилизируемой.
R > 0 и .
BaR − 1NT) не имеет ненаблюдаемого режима на воображаемой оси (или единичной окружности за дискретное время).
lqi поддерживает дескрипторные модели с неингулярными E. Выходные данные S из lqi - решение уравнения Риккати для эквивалентной явной модели «состояние-пространство»
E − 1Bu
[1] П. К. Янг и Дж. К. Виллемс, «Подход к проблеме линейного многомерного сервомеханизма», International Journal of Control, Volume 15, Issue 5, May 1972, pages 961-979.