lqg

Линейно-квадратично-гауссова (LQG) конструкция

Синтаксис

reg = lqg(sys,QXU,QWV) reg = lqg(sys,QXU,QWV,QI) reg = lqg(sys,QXU,QWV,QI,'1dof') reg = lqg(sys,QXU,QWV,QI,'2dof') reg = lqg(___,'current') [reg,info] = lqg(___)

Описание

reg = lqg(sys,QXU,QWV) вычисляет оптимальный линейно-квадратично-гауссовый (LQG) регулятор reg задана модель состояния-пространства sys завода и матриц взвешивания QXU и QWV. Динамический регулятор reg использует измерения y для генерации управляющего сигнала u, который регулирует y вокруг нулевого значения. Используйте положительную обратную связь для подключения регулятора к выходу установки y.

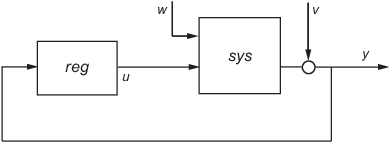
Регулятор LQG минимизирует функцию затрат

$\underset{}{} \frac{}{}_{}^{}^{}^{}_{} \begin{matrix} \end{matrix} J=E{limτ→∞1τ∫0τ[xT,uT]Qxu[xu]dt}$

с учетом уравнений растений

$\begin{matrix} dx/dt = Ax + \\ Bu + wy = \end{matrix}$ Cx + Du + v

где технологический шум w и измерительный шум v - гауссовы белые шумы с ковариацией:

$E (\begin{matrix} [ \end{matrix} \begin{matrix} wv]\cdot[w'v \end{matrix}']) =$ QWV

reg = lqg(sys,QXU,QWV,QI) использует команду r уставки и измерения y для генерации управляющего сигнала u. reg имеет интегральное действие, чтобы гарантировать, что y отслеживает команду r.

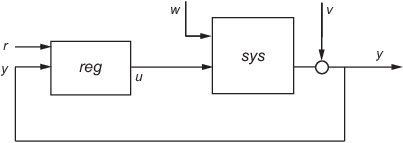
Сервоконтроллер LQG сводит к минимуму функцию затрат

$\underset{}{} \frac{}{}_{}^{J=E{limτ→∞1τ∫0τ} ([^{} xT,^{} {uT}_{]} \begin{matrix} Qxu \end{matrix} [_{xu}^{]}_{+}_{}$ xiTQixi) dt}

где _xi - интеграл ошибки отслеживания r-y. Для систем MIMO r, y и _xi должны иметь одинаковую длину.

reg = lqg(sys,QXU,QWV,QI,'1dof') вычисляет сервоконтроллер с одной степенью свободы, который принимает e = r-y, а не [r; y] в качестве входных данных.

reg = lqg(sys,QXU,QWV,QI,'2dof') эквивалентно LQG(sys,QXU,QWV,QI) и создает сервоконтроллер с двумя степенями свободы, показанный ранее.

reg = lqg(___,'current') использует «текущий» оценщик Калмана, который использует x [n 'n] в качестве оценки состояния при вычислении регулятора LQG для дискретно-временной системы.

[reg,info] = lqg(___) возвращает матрицы усиления контроллера и оценщика в структуре info для любого из предыдущих синтаксисов. Можно использовать выигрыши контроллера и оценщика, например, для реализации контроллера в форме наблюдателя. Дополнительные сведения см. в разделе Алгоритмы.

Примеры

Линейно-квадратично-гауссовый (LQG) регулятор и серворегулятор

В этом примере показано, как сконструировать линейно-квадратично-гауссовый (LQG) регулятор, серворегулятор LQG с одной степенью свободы и серворегулятор LQG с двумя степенями свободы для следующей системы.

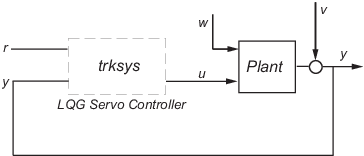
Установка имеет три состояния (x), два управляющих входа (u), три случайных входа (w), один выход (y), шум измерения для выхода (v) и следующие уравнения состояния и измерения.

$\begin{array}{l} \frac{}{dxdt} = Ax + \\ Bu + wy = \end{array}$ Cx + Du + v

где

$\begin{array}{l} A = \begin{matrix} [ \end{matrix} 010001100] B \begin{matrix} = [ \\ 0,3101 & − \end{matrix} \\ \begin{matrix} 0,30,9] & C = \end{matrix} [\begin{matrix} 1,91,31] & D = \end{matrix} [ \end{array}$ 0,53 − 0,61]

Система имеет следующие данные ковариации шума:

$\begin{array}{l} _{Qn} = E^{(} wwT \begin{matrix} ) & = \\ [ \end{matrix} \\ _{} 420210001]^{Rn} = E \end{array}$ (vvT) = 0,7

Для регулятора используйте следующую функцию затрат, чтобы определить компромисс между эффективностью регулирования и усилиями по контролю:

$J (u)_{}^{} =∫0∞ (0^{} .^{} 1xTx \begin{matrix} + \end{matrix} uT [$ 1002] u) dt

Для сервоконтроллеров используйте следующую функцию затрат, чтобы определить компромисс между производительностью трекера и усилиями по управлению:

$J (u)_{}^{} =∫0∞ (0^{} ._{}^{1xTx} +^{} \begin{matrix} x2 \\ + \end{matrix} uT [$ 1002] u) dt

Для проектирования контроллеров LQG для этой системы:

Создайте систему state-space, введя в окне MATLAB Command Window следующее:

A = [0 1 0;0 0 1;1 0 0];    
B = [0.3 1;0 1;-0.3 0.9];
C = [1.9 1.3 1];  
D = [0.53 -0.61];
sys = ss(A,B,C,D);

Определите ковариационные данные шума и матрицы взвешивания, введя следующие команды:

nx = 3;    %Number of states
ny = 1;    %Number of outputs
Qn = [4 2 0; 2 1 0; 0 0 1];
Rn = 0.7;
R = [1 0;0 2]
QXU = blkdiag(0.1*eye(nx),R);
QWV = blkdiag(Qn,Rn);
QI = eye(ny);

Сформируйте регулятор LQG, набрав следующую команду:

KLQG = lqg(sys,QXU,QWV)

Данная команда возвращает следующий регулятор LQG:

A = 
           x1_e    x2_e    x3_e
   x1_e  -6.212  -3.814  -4.136
   x2_e  -4.038  -3.196  -1.791
   x3_e  -1.418  -1.973  -1.766
 
B = 
             y1
   x1_e   2.365
   x2_e   1.432
   x3_e  0.7684
 
C = 
            x1_e       x2_e       x3_e
   u1   -0.02904  0.0008272     0.0303
   u2    -0.7147    -0.7115    -0.7132
 
D = 
       y1
   u1   0
   u2   0
 
Input groups:              
       Name        Channels
    Measurement       1    
                           
Output groups:             
      Name      Channels   
    Controls      1,2      
                           
Continuous-time model.

Сформируйте сервоконтроллер LQG с одной степенью свободы, введя следующую команду:

KLQG1 = lqg(sys,QXU,QWV,QI,'1dof')

Эта команда возвращает следующий контроллер сервопривода LQG:

A = 
           x1_e    x2_e    x3_e     xi1
   x1_e  -7.626  -5.068  -4.891  0.9018
   x2_e  -5.108  -4.146  -2.362  0.6762
   x3_e  -2.121  -2.604  -2.141  0.4088
   xi1        0       0       0       0
 
B = 
              e1
   x1_e   -2.365
   x2_e   -1.432
   x3_e  -0.7684
   xi1         1
 
C = 
          x1_e     x2_e     x3_e      xi1
   u1  -0.5388  -0.4173  -0.2481   0.5578
   u2   -1.492   -1.388   -1.131   0.5869
 
D = 
       e1
   u1   0
   u2   0
 
Input groups:           
    Name     Channels   
    Error       1       
                        
Output groups:          
      Name      Channels
    Controls      1,2   
                        
Continuous-time model.

Сформируйте сервоконтроллер LQG с двумя степенями свободы, введя следующую команду:

KLQG2 = lqg(sys,QXU,QWV,QI,'2dof')

Эта команда возвращает следующий контроллер сервопривода LQG:

A = 
           x1_e    x2_e    x3_e     xi1
   x1_e  -7.626  -5.068  -4.891  0.9018
   x2_e  -5.108  -4.146  -2.362  0.6762
   x3_e  -2.121  -2.604  -2.141  0.4088
   xi1        0       0       0       0
 
B = 
             r1      y1
   x1_e       0   2.365
   x2_e       0   1.432
   x3_e       0  0.7684
   xi1        1      -1
 
C = 
          x1_e     x2_e     x3_e      xi1
   u1  -0.5388  -0.4173  -0.2481   0.5578
   u2   -1.492   -1.388   -1.131   0.5869
 
D = 
       r1  y1
   u1   0   0
   u2   0   0
 
Input groups:              
       Name        Channels
     Setpoint         1    
    Measurement       2    
                           
Output groups:             
      Name      Channels   
    Controls      1,2      
                           
Continuous-time model.

Совет

lqg может использоваться как для установок непрерывного, так и дискретного времени. В дискретное время, lqg по умолчанию использует x [n 'n-1] в качестве оценки состояния. Чтобы использовать x [n 'n] в качестве оценки состояния и вычислить оптимальный контроллер LQG, используйте 'current' входной аргумент. Подробнее об оценщиках состояния см. kalman.
Для вычисления регулятора LQG lqg использует команды lqr и kalman. Чтобы вычислить сервоконтроллер, lqg использует команды lqi и kalman.
Если требуется больше гибкости при проектировании регуляторов, можно использовать lqr, kalman, и lqgreg команды. Если требуется больше гибкости при конструировании сервоконтроллеров, можно использовать lqi, kalman, и lqgtrack команды. Дополнительные сведения об использовании этих команд и о том, как их использовать, см. в разделе Линейная-квадратично-гауссова (LQG) Конструкция регулирования и линейно-квадратично-гауссова (LQG) Конструкция сервоконтроллера с интегральным действием.

Алгоритмы

Уравнения контроллера:

Для непрерывного времени:
$\begin{matrix} _{dxe} =_{} Axe + Bu +_{L} (y \\ -_{Cxe}_{-}_{Du})_{} \end{matrix}$ u = − Kxxe − Kixi
Для дискретного времени:
$x [n + 1 | n] = Ax [n 'n - 1] + Bu [n] + L (y [n]$ − Cx [n' n − 1] − Du [n])
- Задержанный оценщик:
  $u [n] =_{} - Kxx [{n 'n}_{} -_{} 1]$ − Кикси [n]
- Текущий оценщик:
  $\begin{matrix} u [n] =_{} - Kxx [_{} {n 'n}_{]} -_{} Kixi [n] \\ -_{} Kww [n' n] =_{-}_{} Kxx [_{n 'n}_{-} 1_{]}_{-}_{Kixi} [n \end{matrix}$ ] − (KxMx + KwMw) yinn [n]
  $_{yinn} [n] = y [n] - Cx [n 'n -$ 1] − Du [n]

Здесь,

A, B, C и D - матрицы состояния-пространства регулятора LQG, reg.
_xi является интегралом ошибки отслеживания r-y.
_Kx, _Kw, _Ki, L, _Mx и _Mw являются матрицами усиления контроллера и оценщика, возвращенными в info.

См. также

care | dare | kalman | lqi | lqr | lqry | ss

Представлен до R2006a

Документация

lqg