Form Linear-Quadratic-Gaussian (LQG) сервоконтроллер
C = lqgtrack(kest,k)
C = lqgtrack(kest,k,'2dof')
C = lqgtrack(kest,k,'1dof')
C = lqgtrack(kest,k,...CONTROLS)
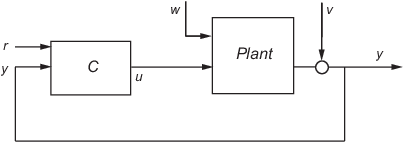
lqgtrack формирует контроллер сервоконтроллера Linear-Quadratic-Gaussian (LQG) с интегральным действием для контура, показанного на следующем рисунке. Этот компенсатор гарантирует, что выходной сигнал y отслеживает опорную команду r и отклоняет нарушения процесса w и шум измерения v. lqgtrack предполагает, что r и y имеют одинаковую длину.
Примечание
Всегда используйте положительную обратную связь для подключения сервоконтроллера LQG C к выходу установки y.
C = lqgtrack(kest,k) образует серворегулятор LQG с двумя степенями свободы C путем подключения оценщика Калмана kest и коэффициент усиления обратной связи о состоянии k, как показано на следующем рисунке. C имеет входы ] и генерирует команду ^; xi]где x ^ - оценка Калмана состояния растения, а xi - выход интегратора.
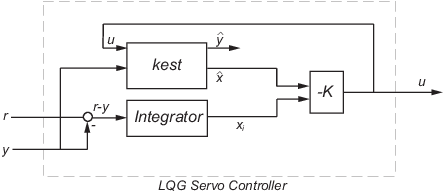
Размер матрицы усиления k определяет длину xi xi, y и r, которые имеют одинаковую длину.
Уравнения состояния-пространства сервоконтроллера LQG с двумя степенями свободы:
Kx − Ki] [x ^ xi]
Примечание
Синтаксис C = lqgtrack(kest,k,'2dof') эквивалентно C = lqgtrack(kest,k).
C = lqgtrack(kest,k,'1dof') образует сервоконтроллер LQG с одной степенью свободы C которая принимает ошибку отслеживания e = r-y в качестве входных данных вместо [r; y], как показано на следующем рисунке.
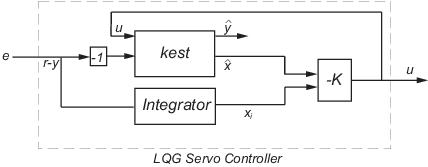
Уравнения состояния-пространства сервоконтроллера LQG с одной степенью свободы:
− Ki] [x ^ xi]
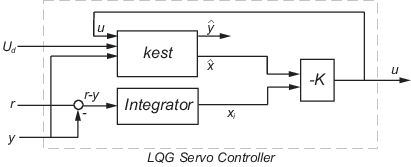
C = lqgtrack(kest,k,...CONTROLS) формирует сервоконтроллер LQG C при оценке Калмана kest имеет доступ к дополнительным известным (детерминированным) командам Ud установки. В индексном векторе CONTROLS, указать, какие входы kest являются каналами управления u. Результирующий компенсатор C имеет входы
[Ud; r; y] в случае с двумя степенями свободы
[Ud; e] в случае одной степени свободы
Соответствующая структура компенсатора для случаев с двумя степенями свободы представлена на следующем рисунке.
См. пример Проектирование сервоконтроллера LQG.
Вы можете использовать lqgtrack как для систем непрерывного, так и дискретного времени.
В дискретно-временных системах интеграторы основаны на прямом Euler (см. lqi для получения подробной информации). Оценка состояния ^ является либо x [n 'n], либо x [n' n-1], в зависимости от типа оценщика ( см.kalman для получения подробной информации).
Для установки дискретного времени с уравнениями:
[n] + v [n] {Измерения}
подключение «текущего» оценщика Калмана к коэффициенту усиления LQR является оптимальным только тогда, когда ′) = 0 и y [n] не зависит от w [n] (H = 0). Если эти условия не выполняются, вычислите оптимальный контроллер LQG с помощьюlqg.