Эксперимент с некоторыми методами сплайновой аппроксимации
splinetool - графический интерфейс пользователя (GUI), начальное меню которого предоставляет различные варианты выбора данных, включая возможность импорта некоторых данных из рабочей области.
Запустите этот код, чтобы запустить графический интерфейс splinetool и поэкспериментировать с шумными данными.
x = linspace(1,pi,101); y = cos(x)+(rand(size(x))-.5)/10; splinetool(x,y)
Целью этого примера является изучение различных конечных условий, доступных с интерполяцией кубических сплайнов:
Напечатать splinetool в командной строке.
Выберите Импорт собственных данных с первого экрана и примите функцию по умолчанию. Появится следующий экран.
По умолчанию показана аппроксимация кубического сплайна с конечным условием «не а-узел».
Вектор x сайтов данных linspace(0,2*pi,31) и значения cos(x). Это отличается от простого предоставления вектора y значений в том смысле, что косинусная функция явно записана в качестве базовой функции. Поэтому ошибка, показанная на графике, является ошибкой сплайна в виде аппроксимации косинуса, а не в виде аппроксимации заданных значений. Обратите внимание на полученную относительно большую ошибку, о 5e-5, рядом с конечными точками.
Для сравнения выполните следующие действия.
Щелкните Создать в списке аппроксимаций.
В окне Метод аппроксимации (Approximation method) выберите в списке Условия окончания (End conditions)
Поскольку первая производная косинусной функции является синусоидальной, отрегулируйте значения первой производной до их известных значений ноль как на левом, так и на правом конце.
Эта процедура приводит к отображению, показанному ниже (после использования мыши для дальнейшего перемещения легенды вниз). Обратите внимание, что наклон правого конца равен нулю только до скругления. Bottomline сообщает, что функция панели инструментов csape использовался для создания сплайна.
Будьте впечатлены улучшением ошибки, которая только о 5e-6.
Для дальнейшего сравнения выполните следующие действия:
Щелкните Создать в списке аппроксимаций.
В методе аппроксимации выберите натуральный из списка условий конца.
Обратите внимание на ухудшение аппроксимации вблизи концов, ошибка около 2e-3, что намного хуже, чем при не узловых концевых условиях.
Для окончательного сравнения выполните следующие действия.
Щелкните Создать в списке аппроксимаций.
Поскольку известно, что косинусная функция является периодической, в методе аппроксимации выберите периодическую из списка условий конца.
Обратите внимание на резкое улучшение аппроксимации, возвращающееся к ошибке около 5e-6, особенно по сравнению с естественными конечными условиями.
В этом примере используется интерполяция кубических сплайнов и аппроксимация наименьших квадратов для определения оценки начального ускорения для автомобиля с лобовым сопротивлением:
Напечатать splinetool в командной строке или если графический интерфейс пользователя уже запущен, щелкните Файл > Перезапустить.
Выберите данные Richard Tapia drag racing. Эти данные показывают расстояние, пройденное тормозным автомобилем в зависимости от времени. Окно сообщения просит оценить начальное ускорение, установив начальную скорость равной нулю. Нажмите кнопку ОК или используйте пробел или Enter для удаления окна сообщения.
В окне Метод аппроксимации (Approximation method) выберите в списке Условия окончания (End conditions)
Отрегулируйте начальную скорость, изменив первую производную в левой конечной точке на ноль.
Найдите значение начального ускорения, которое задается значением второй производной в левой конечной точке. Можно переключаться между первой и второй производными в этой конечной точке, нажав левую кнопку. Значение второй производной должно быть около 187 в выбранных единицах. Выберите меню «Просмотр» > «Показать
вторую производную», чтобы просмотреть это графически.
Для сравнения щелкните Создать (New), затем выберите Аппроксимация методом наименьших квадратов (Least-Squares Approximation) в качестве метода аппроксимации. С помощью этого метода невозможно определить конечные условия. Вместо этого можно изменить порядок метода. Убедитесь, что начальное ускорение близко к значению кубической интерполяции.
Результаты этой процедуры показаны ниже.
В этом примере рекомендуется разместить пять внутренних узлов таким образом, чтобы аппроксимация наименьших квадратов к этим данным кубическими сплайнами имела абсолютную ошибку, не большую, чем .04 везде:
Напечатать splinetool в командной строке или если графический интерфейс пользователя уже запущен, щелкните Файл > Перезапустить.
Выберите Данные по теплу титана.
В качестве метода аппроксимации выберите Аппроксимация наименьших квадратов.
Обратите внимание, как плохо это аппроксимирует данные, поскольку отсутствуют внутренние узлы. Чтобы просмотреть текущие узлы и добавить новые узлы, выберите узлы из данных, разрывы/узлы, веса. Узлы теперь перечисляются в узлах, а также отображаются на графике данных в виде вертикальных линий. Обратите внимание, что есть только два концевых узла, каждый с кратностью 4.
Щелкните правой кнопкой мыши график данных и выберите Добавить узел (Add Knot). Это поднимает перекрестие, чтобы вы двигались с помощью мыши. Его точное горизонтальное расположение показано в поле редактирования под списком узлов. Щелчок мыши помещает новый узел в текущее место перекрестия. Одной из возможных стратегий является размещение дополнительного узла в месте максимальной абсолютной ошибки, как показано на вспомогательном графике под графом данных.
Если щелкнуть правой кнопкой мыши и выбрать Реплицировать узел (Replicate Knot), будет увеличена кратность текущего узла, что показано его повторяющимся появлением в узлах (Knots). Если вам не нравится конкретный узел, вы можете удалить его. Чтобы удалить конкретный узел, необходимо сначала выбрать его в списке узлов или графике данных, а затем щелкнуть правой кнопкой мыши на графике и выбрать Удалить узел (Delete Knot).
Можно также запросить приближение, используя шесть полиномиальных частей, что соответствует пяти внутренним узлам. Для этого введите 6 # шт. в данных, разрывах/узлах, весах.
После того, как у вас есть пять внутренних узлов, попробуйте сделать ошибку еще меньше, перемещая узлы. Для этого выберите узел, который требуется переместить, щелкнув его вертикальную линию на графике, затем используйте управление интерфейсом ниже узлов в данных, разрывов/узлов, весов и наблюдать, как ошибка изменяется с движением узла. Можно также использовать поле редактирования для перезаписи текущего расположения узла. Можно также попытаться настроить, что перераспределяет текущую последовательность узлов.
Используйте команду Реплицировать в списке аппроксимаций (Replicate in List of approximations), чтобы сохранить любое хорошее распределение узлов для последующего использования. Переименование реплицированного приближения в lstsqr с помощью команды «Переименовать». Чтобы вернуться к исходному приближению, щелкните его имя в списке приближений.
В этом примере выполняется эксперимент со сглаживанием сплайнов:
Напечатать splinetool в командной строке или, если графический интерфейс уже запущен, щелкните Файл > Перезапустить.
Выберите Данные по теплу титана.
В методе аппроксимации выберите «Сглаживание сплайна».
Параметр варьирования (Vary Parameter) между 0 и 1, который изменяет аппроксимацию с прямолинейной аппроксимации наименьших квадратов на интерполяцию «натурального» кубического сплайна.
Варьировать допуск между 0 и некоторым большим значением, даже inf. Аппроксимация изменяется от наилучшего возможного, «натурального» кубического сплайнового интерполятора, к прямолинейному аппроксимации наименьших квадратов.
При увеличении значения параметра или уменьшении значения допуска ошибка уменьшается. Однако меньшая погрешность соответствует большей шероховатости, измеряемой размером второй производной. Для этого выберите «Просмотр» > «Показать вторую производную» и снова измените значения параметров и допусков.
Этот шаг изменяет веса в измерении ошибки, чтобы заставить аппроксимацию пройти через конкретную точку данных.
Установить допуск в значение 0.2. Обратите внимание, что аппроксимация не проходит через самую высокую точку данных. Чтобы увидеть большую ошибку на этом сайте, выберите Просмотр > Ошибка.
Для принудительного прохождения сглаживающего сплайна через эту точку выберите «Веса ошибок из данных», «Разрывы/узлы», «Веса».
Щелкните по самой высокой точке данных на графике и обратите внимание на ее сайт, который указан в Sites and Values.
Используйте поле редактирования под списком весов, чтобы изменить текущий вес на 1000. Обратите внимание на то, насколько близок сглаживающий сплайн к этой самой высокой точке данных, и на уменьшение погрешности на этой площадке. Включите сетку по меню «Сервис» > «Сетка», чтобы быстрее обнаружить ошибку на этом сайте.
Этот этап изменяет веса в измерении шероховатости, чтобы обеспечить более точное, но менее гладкое приближение в области пика, в то же время настаивая на более гладком, следовательно, менее точном приближении от области пика.
Выберите Прыжки в вес шероховатости из данных, разрывы/узлы, веса.
Выберите меню «Просмотр» > «Показать вторую производную»
Выберите любую точку данных слева от пика в данных.
Установить переход на выбранном сайте в значение -1 путем изменения его значения в поле редактирования под ним. Поскольку вес шероховатости для самого первого интервала месторасположения равен 1, необходимо только что установить вес шероховатости справа от выделенного месторасположения равным 0. Соответственно, вторая производная стала относительно маленькой слева от этого участка.
Выберите любую точку данных справа от пика в данных.
Задайте для перехода через выбранный сайт значение 1. Поскольку вес шероховатости слева от выделенной площадки равен 0, необходимо только что установить вес шероховатости справа от выделенной площадки равным 1. Соответственно, вторая производная стала относительно небольшой справа от этого участка. Общий эффект - очень гладкая, но не очень точная посадка вдали от пика, в то время как в области пика посадка сплайна намного лучше, но вторая производная намного больше, как показано на вспомогательном графике ниже.
На участках, где происходит скачок веса шероховатости, имеется соответствующий скачок во второй производной. При увеличении значения параметра погрешность по площади пика уменьшается, но вторая производная остается довольно большой, в то время как противоположная имеет значение в стороне от площади пика.
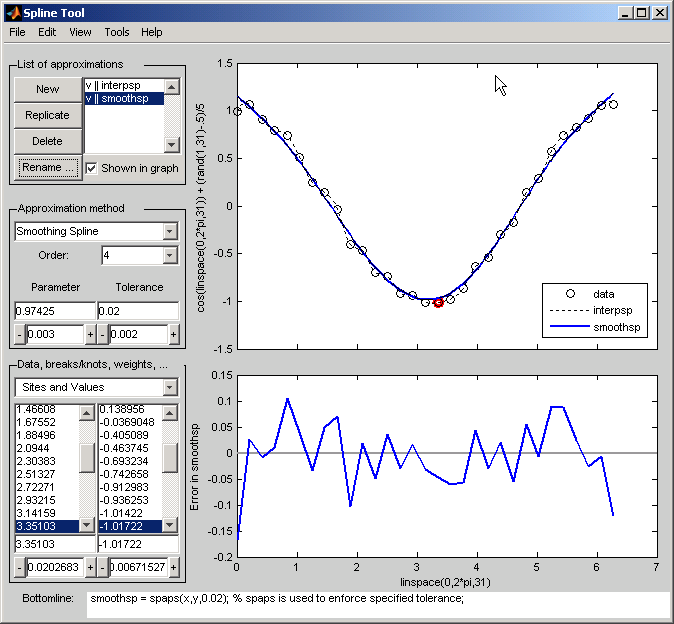
Инструмент «Сплайн» (Spline) показан на следующем рисунке, на котором сравнивается интерполяция кубического сплайна со сглаживающим сплайном для данных выборки, созданных путем добавления шума к косинусной функции.
Методы аппроксимации
Методы и параметры аппроксимации, поддерживаемые графическим интерфейсом, показаны ниже.
Метод аппроксимации | Выбор |
|---|---|
Кубическая интерполяция сплайна | Настройте тип и значения конечных условий. |
Сглаживание сплайна | Выберите кубический (порядок 4) и квинтический (порядок 6) сплайны. Отрегулируйте значение параметра допуска и/или сглаживания. Отрегулируйте веса в измерениях погрешности и шероховатости. |
Аппроксимация методом наименьших квадратов | Варьируйте порядок от 1 до 14. Порядок по умолчанию равен 4, что дает кубические аппроксимирующие сплайны. Измените количество отрезков полинома. Добавьте и переместите узлы для улучшения посадки. Отрегулируйте веса в измерении ошибок. |
Интерполяция сплайнов | Варьируйте порядок от 2 до 14. Порядок по умолчанию равен 4, что дает интерполяции кубических сплайнов. Если узлы по умолчанию не являются удовлетворительными, их можно перемещать для изменения посадки. |
Графики
Можно создать и сравнить несколько аппроксимаций с одними и теми же данными. Одно из приближений всегда помечается как «текущее» с использованием более толстой ширины линии. Доступны следующие дисплеи:
График данных. Он показывает:
Данные
Аппроксимации, выбранные для отображения в списке аппроксимаций
Текущая последовательность узлов или текущая последовательность разрывов
Вспомогательный график (если просматривается) для текущего приближения. Этот график можно вызвать, выбрав любой из элементов в меню Вид (View). Здесь показан один из следующих вариантов:
Первая производная
Вторая производная
Ошибка
По умолчанию ошибка представляет собой разницу между заданными значениями данных и значением аппроксимации в узлах данных. В частности, ошибка равна нулю (вплоть до округления), когда аппроксимация является интерполятором. Однако если ввести значения данных, указав функцию, то отображаемая ошибка представляет собой разницу между этой функцией и текущим приближением. Это также происходит, если изменить обозначение y графа данных на имя функции.
Параметры меню
Аннотировать и печатать графики можно с помощью меню Файл (File) > Печать на рисунок (Print to Figure).
Данные и аппроксимации можно экспортировать в рабочую область для дальнейшего использования или анализа с помощью меню «Файл» > «Экспорт данных» и «Файл» > «Экспорт сплайна» соответственно.
С помощью меню Файл (File) > Создать код (Generate Code) можно создать файл функции, который можно использовать для создания из исходных данных любого или всех отображаемых в данный момент графиков. Этот файл также предоставляет запись команд, используемых для создания текущего графика (графиков).
Перед дальнейшим экспериментом можно сохранить текущее приближение с помощью кнопки «Репликация». Если позже нажать на сохраненное таким образом приближение, splinetool восстанавливает все так, как было, включая данные, использованные при построении сохраненного приближения. Это верно, даже если после сохранения этого приближения данные были отредактированы во время работы с другими приближениями.
Можно добавить, удалить или переместить данные, узлы и разрывы, щелкнув правой кнопкой мыши на графике или выбрав соответствующий пункт в меню Править (Edit).
Можно переключить сетку или легенду на графике (графиках) с помощью меню Сервис (Tools).