Решить линейную систему уравнений с помощью рекурсии Левинсона-Дурбина
Математические функции/матрицы и линейные алгебры/решатели линейных систем
dspsolvers
Блок Левинсона - Дурбина решает систему линейных уравнений n-го порядка
Ra = b
в случаях, когда:
R - эрмитова положительно-определённая матрица Тёплица.
b идентичен первой колонке R, сдвинутой на один элемент и имеющей противоположный знак.
⋮a (n + 1)] = [− r (2) − r (3) ⋮−r (n + 1)]
Вход в блок, r = [r(1) r(2) ... r(n+1)], может быть вектором или матрицей. Если вход является матрицей, блок обрабатывает каждый столбец как независимый канал и решает его отдельно. Каждый канал входа содержит запаздывания от 0 до n автокорреляционной последовательности, которые появляются в матрице R.
Блок может выводить полиномиальные коэффициенты A, коэффициенты отражения K и мощность ошибки предсказания P в различных комбинациях. Параметр Output (s) позволяет включить выходы A и K, выбрав одну из следующих настроек:
A - Для каждого канала выходы порта A A = [1 a(2) a(3) ... a(n+1)], решение уравнения Левинсона-Дурбина. А имеет тот же размер, что и вход. Можно также просматривать элементы каждого выходного канала как коэффициенты процесса авторегрессии n-го порядка (AR).
K - Для каждого канала выход порта K K = [k(1) k(2) ... k(n)], который содержит n коэффициентов отражения и имеет ту же размерность, что и вход, за вычетом одного элемента. Скалярный входной канал вызывает ошибку при выборе K. Коэффициенты отражения можно использовать для реализации представления решетки процесса AR, описанного ниже на этой странице.
A and K - Блок выводит оба представления на соответствующие порты. Скалярный входной канал вызывает ошибку при выборе A and K.
Установите флажок Выходная мощность ошибки предсказания (P), чтобы вывести мощность ошибки предсказания для каждого канала, Р. Для каждого канала P представляет мощность выходного сигнала КИХ-фильтра с отводами А и входной автокорреляцией, описанной как r, где A представляет фильтр ошибки предсказания, а r является входом в блок. В этом случае А является отбеливающим фильтром. Р имеет один элемент на один входной канал.
При установке флажка Если значение запаздывания 0 равно нулю, A = [1 ноль], K = [нули], P = 0 (по умолчанию), входной канал, r(1) элемент равен нулю создает нулевой выходной сигнал. При снятии этого флажка ввод с r(1) = 0 производит NaNs в выходных данных. В общем, вход с r(1) = 0 недопустим, поскольку он не создает положительно-определенную матрицу R. Однако часто блоки получают нулевые входные данные в начале моделирования. Флажок позволяет избежать распространения NaNs в этот период.
Одним из применений формулировки Левинсона-Дурбина, реализованной этим блоком, является задача Юле-Уокера AR, которая касается моделирования неизвестной системы как авторегрессионного процесса. Вы бы смоделировали такой процесс, как выход полюсного БИХ фильтра с белым гауссовым шумом. В задаче Юле-Уокера использование автокорреляционной последовательности сигнала для получения оптимальной оценки приводит к уравнению Ra = b типа, показанного выше, которое наиболее эффективно решается рекурсией Левинсона-Дурбина. В этом случае вход в блок представляет автокорреляционную последовательность с r(1) является значением нулевого запаздывания. Выходной сигнал A-порта блока затем содержит коэффициенты авторегрессионного процесса, который оптимально моделирует систему. Коэффициенты упорядочены в степени убывания z, и процесс AR является минимальной фазой. Ошибка прогнозирования G определяет коэффициент усиления для неизвестной системы, где P:
. + a (n + 1) z − n
Выходной сигнал в K-порте блока содержит соответствующие коэффициенты отражения, [k(1) k(2) ... k(n)], для реализации решетки этого БИХ фильтра. Блок оценки AR Юле-Уокера реализует этот основанный на автокорреляции метод для оценки модели AR, в то время как блок метода Юле-Уокера расширяет метод до спектральной оценки.
Другим распространенным применением алгоритма Левинсона-Дурбина является линейное предиктивное кодирование, которое касается нахождения коэффициентов процесса скользящего среднего (МА) (или КИХ-фильтра), который предсказывает следующее значение сигнала из текущей выборки сигнала и конечное число прошлых выборок. В этом случае вход в блок представляет автокорреляционную последовательность сигнала, где r(1) является значением нулевого запаздывания, и выходной сигнал в A-порту блока содержит коэффициенты процесса предсказания MA (в степени убывания z).
... a (n + 1) z − n
Эти коэффициенты решают следующую задачу оптимизации:
мин
И снова выходной сигнал в K-порте блока содержит соответствующие коэффициенты отражения. [k(1) k(2) ... k(n)], для реализации решетки этого FIR-фильтра. Блок LPC автокорреляции в библиотеке линейного прогнозирования реализует этот основанный на автокорреляции метод прогнозирования.
Диаграммы в этом разделе показывают типы данных, используемые в блоке Левинсона-Дурбина для сигналов с фиксированной точкой.
После инициализации блок выполняет n обновлений. При обновлении (j + 1),
r (j − i + 1)
На следующей диаграмме показаны типы данных с фиксированной точкой, используемые в этом расчете:
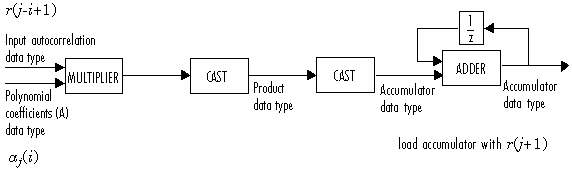
Затем блок обновляет коэффициенты K отражения в соответствии с
аккумуляторе/Pj
Затем блок обновляет мощность P ошибки прогнозирования в соответствии с
)
На следующей диаграмме показаны типы данных с фиксированной точкой, используемые в этом расчете:
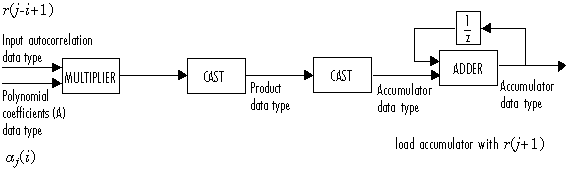
Полиномиальные коэффициенты А затем обновляются в соответствии с
(j−1+i))
На этой схеме показаны типы данных с фиксированной точкой, используемые в этом расчете:
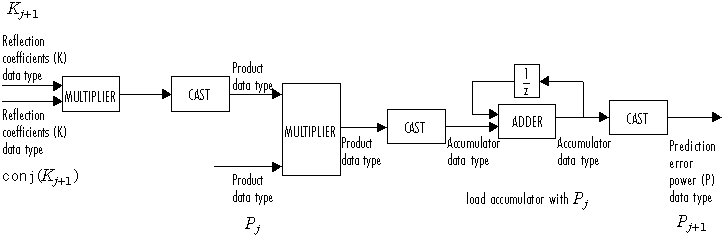
Алгоритм требует операций O (n2) для каждого входного канала. Поэтому эта реализация является гораздо более эффективной для больших n, чем стандартное гауссово исключение, которое требует O (n3) операций на канал.
Главная вкладка
Задайте представление решения Ra = b для вывода: коэффициенты модели (A), коэффициенты отражения (K) или оба (A and K). Если вход является скалярным вектором или вектором строки, необходимо задать для этого параметра значение A.
Выберите для вывода ошибки прогнозирования на порт P.
При установке этого флажка и первого элемента ввода, r(1), равно нулю, блок выводит следующие векторы, в зависимости от обстоятельств:
A = [1 zeros(1,n)]
K = [zeros(1,n)]
P = 0
При снятии этого флажка блок выводит вектор NaNs для каждого канала, r(1) элемент равен нулю.
Вкладка «Типы данных»
Примечание
Наследование с плавающей запятой имеет приоритет над параметрами типа данных, определенными на этой панели. Если входные данные имеют плавающую точку, блок игнорирует эти настройки, и все внутренние типы данных являются плавающей точкой.
Укажите режим округления для операций с фиксированной точкой как одно из следующих:
Floor
Ceiling
Convergent
Nearest
Round
Simplest
Zero
Дополнительные сведения см. в разделе Режим округления.
При выборе этого параметра блок насыщает результат операции с фиксированной точкой. При сбросе этого параметра блок переносит результат операции с фиксированной точкой. Для получения подробной информации о saturate и wrap, см. режим переполнения для операций с фиксированной точкой.
Укажите тип выходных данных продукта. Примеры использования типа выходных данных продукта в этом блоке приведены в разделах Типы данных с фиксированной точкой и Типы данных умножения. Можно установить для него значение:
Правило, наследующее тип данных, например: Inherit: Same as input
Выражение, которое вычисляет допустимый тип данных, например: fixdt(1,16,0)
Нажмите кнопку Show data type assistant (Показать помощник по типам данных
), чтобы отобразить помощник по типам данных, который помогает задать параметр вывода продукта.
Дополнительные сведения см. в разделе Определение типов данных с помощью помощника по типам данных (Simulink).
Укажите тип данных накопителя. Примеры использования типа данных накопителя в этом блоке приведены в разделе Типы данных с фиксированной точкой. Можно установить для него значение:
Правило, наследующее тип данных, например: Inherit: Same as input
Правило, наследующее тип данных, например: Inherit: Same as product output
Выражение, которое вычисляет допустимый тип данных, например: fixdt(1,16,0)
Нажмите кнопку Show data type assistant (Показать помощник по типам данных) для отображения помощника по типам данных, который поможет установить параметр Accumulator.
Дополнительные сведения см. в разделе Определение типов данных с помощью помощника по типам данных (Simulink).
Укажите тип данных полиномиальных коэффициентов (A). Примеры использования типа данных A в этом блоке приведены в разделе «Типы данных с фиксированной точкой». Можно задать выражение, которое вычисляет допустимый тип данных, например: fixdt(1,16,15).
Нажмите кнопку Show data type assistant (Показать помощник по типам данных) для отображения помощника по типам данных, который поможет задать параметр A.
Дополнительные сведения см. в разделе Определение типов данных с помощью помощника по типам данных (Simulink).
Укажите тип данных полиномиальных коэффициентов (A). Примеры использования типа данных K в этом блоке приведены в разделе «Типы данных с фиксированной точкой». Можно задать выражение, которое вычисляет допустимый тип данных, например: fixdt(1,16,15).
Нажмите кнопку Show data type assistant (Показать помощник по типам данных) для отображения помощника по типам данных, который поможет установить параметр K.
Дополнительные сведения см. в разделе Определение типов данных с помощью помощника по типам данных (Simulink).
Укажите тип данных мощности ошибки прогнозирования (P). Примеры использования типа данных P в этом блоке приведены в разделе «Типы данных с фиксированной точкой». Можно установить для него значение:
Правило, наследующее тип данных, например: Inherit: Same as input
Выражение, которое вычисляет допустимый тип данных, например: fixdt(1,16,0)
Нажмите кнопку Show data type assistant (Показать помощник по типам данных) для отображения помощника по типам данных, который поможет установить параметр P.
Дополнительные сведения см. в разделе Определение типов данных с помощью помощника по типам данных (Simulink).
Укажите минимальные значения, которые должны иметь коэффициенты полинома, коэффициенты отражения или мощность ошибки прогнозирования. Значение по умолчанию: [] (не указано). Simulink ® использует это значение для выполнения следующих действий:
Проверка диапазона параметров (см. раздел Указание минимального и максимального значений для параметров блока (Simulink))
Автоматическое масштабирование типов данных с фиксированной точкой
Укажите максимальные значения, которые должны иметь коэффициенты полинома, коэффициенты отражения или мощность ошибки прогнозирования. Значение по умолчанию: [] (не указано). Simulink использует это значение для выполнения следующих действий:
Проверка диапазона параметров (см. раздел Указание минимального и максимального значений для параметров блока (Simulink))
Автоматическое масштабирование типов данных с фиксированной точкой
Выберите этот параметр, чтобы инструменты с фиксированной точкой не переопределяли типы данных, заданные в маске блока.
Голуб, Г. Х. и К. Ф. Ван Займ. Секта. 4.7 в матричных вычислениях. 3-й ред. Балтимор, доктор медицинских наук: Johns Hopkins University Press, 1996.
Ljung, L. Идентификация системы: теория для пользователя. Энглвуд Клиффс, Нью-Джерси: Прентис Холл, 1987. Пгс. 278–280.
Кей, Стивен М. Современная спектральная оценка: теория и применение. Энглвуд Клиффс, Нью-Джерси: Прентис Холл, 1988.
Плавающая точка с двойной точностью
Плавающая точка с одинарной точностью
Фиксированная точка (только подпись)
8-, 16- и 32-разрядные целые числа со знаком