Библиотека «Матрицы» и «Линейная алгебра» предоставляет три больших поддиапазона, содержащих блоки для линейной алгебры; Решатели линейной системы (Linear System Solvers), факторизации матрицы (Matrix Factorizations) и Инверсирование матрицы (Matrix Inverses). Четвертая библиотека, Matrix Operations, предоставляет другие важные блоки для работы с матрицами.
Библиотека решателей линейной системы предоставляет следующие блоки для решения системы линейных уравнений AX = B:
Некоторые из блоков предлагают особые сильные стороны для определенных классов проблем. Например, блок Cholesky Solver приспособлен для квадратной эрмитовой положительной определенной матрицы A, тогда как блок Backward Substraction подходит для верхней треугольной матрицы A.
В следующей модели ex_lusolver_tut блок решателя логической единицы решает уравнение Ax = b, где
− 2 − 1]
и находит х в качестве вектора [-2 0 1]'.
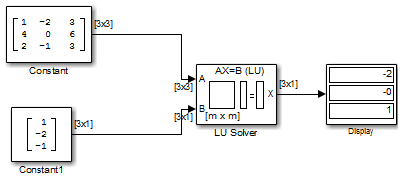
Можно проверить решение с помощью блока Умножение матрицы (Matrix Multiply) для выполнения умножения Ax, как показано в следующей модели ex_matrixmultiply_tut1.
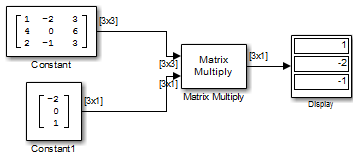
Библиотека матричных факторизаций предоставляет следующие блоки для факторизации различных типов матриц:
Некоторые из блоков предлагают особые сильные стороны для определенных классов проблем. Например, блок факторизации Cholesky подходит для факторизации эрмитовой положительной определенной матрицы на треугольные компоненты, тогда как QR факторизация подходит для факторизации прямоугольной матрицы на унитарные и верхние треугольные компоненты.
В следующей модели ex_lufactorization_tut блок факторизации LU преобразует матрицу Ap в верхнюю и нижнюю треугольные подматрицы U и L, где Ap - строка, эквивалентная входной матрице A, где
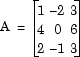
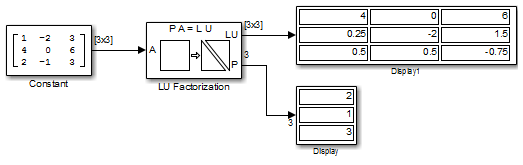
Нижний выход факторизации логической единицы, P, - вектор индекса перестановки, который указывает, что факторизованная матрица Ap генерируется из A путем замены первой и второй строк.
− 13]
Верхний выход модуля факторизации логической единицы, LU, является композитной матрицей, содержащей два субматричных фактора, U и L, произведение LU которой равно Ap.
1000,25100,50,51]
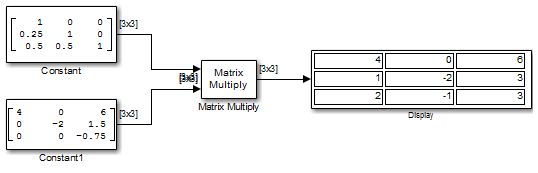
Можно проверить, что LU = Ap с помощью блока «Умножение матрицы» (Matrix Multiply), как показано в следующей модели ex_matrixmultiply_tut2.
Библиотека Matrix Inverses предоставляет следующие блоки для инвертирования различных типов матриц:
В следующей модели ex_luinverse_tut блок LU Inverse вычисляет инверсию входной матрицы A, где
− 13]
и затем формирует произведение A-1A, которое дает идентичную матрицу порядка 3, как и ожидалось.
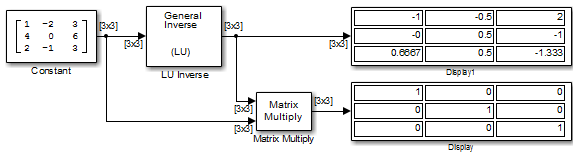
Как показано выше, вычисленная обратная