При подгонке модели временных рядов к данным запаздывающие термины в модели требуют инициализации, как правило, с наблюдениями в начале выборки. Кроме того, чтобы измерить качество прогнозов из модели, необходимо сохранить данные в конце выборки из оценки. Поэтому перед анализом данных разбейте временную базу на три последовательных непересекающихся интервала:
Тремя разделами временной базы для одномерных авторегрессионных моделей интегрированного скользящего среднего (ARIMA) являются периоды предварительной выборки, оценки и прогноза.
Период предварительного отбора - содержит данные, используемые для инициализации запаздывающих значений в модели. Авторегрессивная интегрированная модель скользящего среднего ARIMA (p, D, q) ⨉ (ps, Ds, qs) s требует периода предварительной выборки, содержащего, по меньшей мере, p + D + ps + s наблюдений (см. свойство Parima объект модели). Например, если планируется подогнать модель ARIMA (4,1,1), условное ожидаемое значение Δyt, учитывая его историю, содержит Δyt - 1 = yt - 1 - yt - 2 - Δyt - 4 = yt - 4 - yt - 5. Условное ожидаемое значение Δy6 является функцией от y5 до y1 и, следовательно, вклад вероятности Δy6 требует этих наблюдений. Кроме того, данных о вероятностном вкладе Δy1 через Δy5 не существует. Следовательно, оценка модели требует периода предварительной выборки, по меньшей мере, из пяти временных точек.
Период оценки - содержит наблюдения, к которым явно подходит модель. Количество наблюдений в оценочной выборке является эффективным размером выборки. Для идентификации параметров эффективный размер выборки должен быть, по крайней мере, количеством оцениваемых параметров.
Период прогноза - дополнительный период, в течение которого создаются прогнозы, известный как горизонт прогноза. Этот раздел содержит данные удержания для проверки предсказуемости модели.
Предположим, yt - это серия ответов, а Xt - 3-D экзогенная серия. Рассмотрите возможность подгонки модели yt SARIMAX (p, D, q) ⨉ (ps, Ds, qs) к данным ответа в векторе T-by-1y и экзогенные данные в матрице T-by-3 X. Кроме того, требуется, чтобы горизонт прогноза имел длину K (т. е. требуется сохранить наблюдения K в конце выборки для сравнения с прогнозами из подогнанной модели).
На этом рисунке показаны разделы временной базы для оценки модели. На рисунке J = p + D + ps + s.
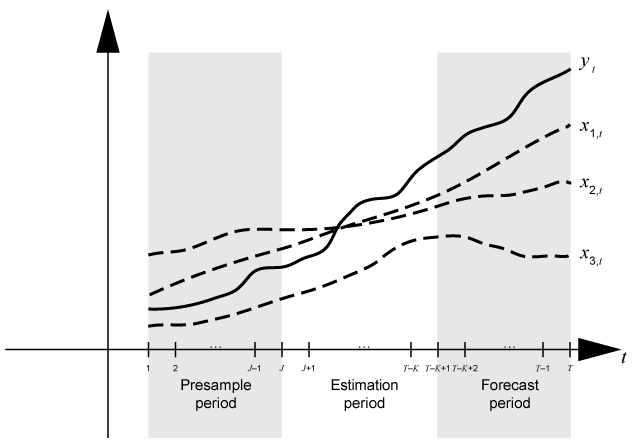
На этом рисунке показаны части массивов, которые соответствуют входным аргументам estimate функции arima модель.
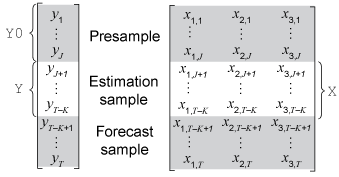
Y является необходимым вводом для указания данных ответа, которым соответствует модель.
'Y0' является необязательным аргументом пары имя-значение для указания данных ответа предварительной выборки. Y0 должен иметь не менее J строк. Чтобы инициализировать модель, estimate использует только последние наблюдения J Y0((end – .J + 1):end)
estimate также принимает предварительные инновации и условные отклонения при указании 'E0' и 'V0' аргументы пары имя-значение. Эти серии не включены в рисунки, но те же принципы распространяются и на них.
'X' является необязательным аргументом пары имя-значение для указания экзогенных данных для компонента регрессии. По умолчанию estimate исключает компонент регрессии из модели независимо от значения коэффициента регрессии Beta в arima шаблон модели.
Для модели без экзогенного компонента регрессии, если не указан Y0, estimate обратная передача модели для требуемых наблюдений предварительного образца. estimate впоследствии подгоняет модель ко всем указанным данным ответа Y. Хотя estimate backcasts для presample по умолчанию, можно извлечь presample из данных и указать его с помощью 'Y0' аргумент пары «имя-значение» для обеспечения estimate инициализирует и подгоняет модель к вашим спецификациям.
При указании 'X', применяются следующие условия:
estimate синхронизируется X и y относительно последнего наблюдения в массивах (T - K на предыдущем рисунке) и применяет только необходимое количество наблюдений к регрессионной составляющей. Это действие подразумевает, что X может иметь больше строк, чем Y.
Если не указать 'Y0', вы должны предоставить по крайней мере J более экзогенные наблюдения, чем ответы. estimate использует дополнительные экзогенные данные предварительной выборки для обратной трансляции модели для ответов предварительной выборки.
При указании 'Y0', estimate использует только последние экзогенные наблюдения, необходимые для соответствия модели (наблюдения от J + 1 до T - K на предыдущем рисунке). estimate игнорирует предварительную выборку экзогенных данных.
Если планируется проверить прогностическую мощность подогнанной модели, перед оценкой необходимо извлечь образец прогноза из набора данных.
В этом примере показано, как разделить временную базу ежемесячного набора данных о пассажирах международных авиакомпаний Data_Airline инициализировать оценку и оценить прогностическую эффективность оценочной модели.
Загрузка и предварительная обработка данных
Загрузите данные.
load Data_AirlineПеременная DataTable - расписание, содержащее временные ряды. PSSG.
Постройте график временных рядов.
plot(DataTable.Time,DataTable.PSSG) xlabel('Time (months)') ylabel('Passenger Counts')

Серия демонстрирует сезонность и экспоненциальный тренд.
Определите, имеются ли в данных отсутствующие значения.
anymissing = sum(ismissing(DataTable))
anymissing = 0
Отсутствуют отсутствующие наблюдения.
Стабилизируйте последовательность, применив преобразование журнала.
StblTT = varfun(@log,DataTable);
База времени секционирования
Рассмотрим модель SARIMA (0,1,1) × (0,1,1) 12 для журнала ежемесячного учета пассажиров с 1949 по 1960 год. Для модели 0 + 1 + 0 + 12 = 13 presample. Одинarima шаблон модели для оценки сохраняет необходимое количество ответов предварительной выборки в свойстве P.
Создайте шаблон модели SARIMA (0,1,1) × (0,1,1) 12 для оценки. Укажите, что константа модели равна0. Проверьте необходимое количество предварительных наблюдений, отображая значение P с использованием точечной нотации.
Mdl = arima('Constant',0,'D',1,'MALags',1,'SMALags',12,... 'Seasonality',12); Mdl.P
ans = 13
Рассмотрим горизонт прогноза в два года (24 месяца). Разбиение данных ответа на предварительные, оценочные и прогнозные выборочные переменные.
fh = 24; % Forecast horizon T = size(StblTT,1); % Total sample size eT = T - Mdl.P - fh; % Effective sample size idxpre = 1:Mdl.P; idxest = (Mdl.P + 1):(T - fh); idxfor = (T - fh + 1):T; y0 = StblTT.log_PSSG(idxpre); % Presample responses y = StblTT.log_PSSG(idxest); % Estimation sample responses yf = StblTT.log_PSSG(idxfor); % Forecast sample responses
Модель оценки
Подгоните модель к оценочной выборке. Укажите предварительный пример с помощью 'Y0' аргумент пары имя-значение.
EstMdl = estimate(Mdl,y,'Y0',y0);
ARIMA(0,1,1) Model Seasonally Integrated with Seasonal MA(12) (Gaussian Distribution):
Value StandardError TStatistic PValue
_________ _____________ __________ __________
Constant 0 0 NaN NaN
MA{1} -0.31781 0.087289 -3.6408 0.00027175
SMA{12} -0.56707 0.10111 -5.6083 2.0434e-08
Variance 0.0014446 0.00018295 7.8962 2.8763e-15
EstMdl является полностью указанным arima модель, представляющая предполагаемую модель SARIMA
1-0.18L12) αt,
где - гауссов со средним значением 0 и дисперсией 0,0019.
Потому что константа 0 в шаблоне модели, estimate рассматривает его как ограничение равенства во время оптимизации. Поэтому выводы о константе не имеют значения.
Прогнозировать модель можно с помощью forecast функция arima путем указания EstMdl и горизонт прогноза fh. Чтобы инициализировать модель для прогнозирования, укажите данные выборки оценки. y с помощью 'Y0' аргумент пары имя-значение.