Мультипликативные спецификации модели ARIMA

Сезонная модель ARIMA без постоянного срока

В этом примере показано, как использовать arima для определения мультипликативной сезонной модели ARIMA (для ежемесячных данных) без постоянного члена.

Укажите мультипликативную сезонную модель ARIMA без постоянного члена,

$(_{} 1-ϕ1L) (_{}^{} 1-Φ12L12) (^{1-L}) 1^{(}_{} 1-L12) {ыт}_{} = (1 +_{}^{θ1L)} (_{1}$ + Θ12L12) αт,

где инновационное распределение является гауссовым с постоянной дисперсией. Здесь ( $1-L)^{1}$ является оператором несезонной дифференциации первой степени и ( $^{1-L12)}$ является оператором сезонной дифференциации первой степени с периодичностью 12.

Mdl = arima('Constant',0,'ARLags',1,'SARLags',12,'D',1,...
            'Seasonality',12,'MALags',1,'SMALags',12)

Mdl = 
  arima with properties:

     Description: "ARIMA(1,1,1) Model Seasonally Integrated with Seasonal AR(12) and MA(12) (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 26
               D: 1
               Q: 13
        Constant: 0
              AR: {NaN} at lag [1]
             SAR: {NaN} at lag [12]
              MA: {NaN} at lag [1]
             SMA: {NaN} at lag [12]
     Seasonality: 12
            Beta: [1×0]
        Variance: NaN

Аргумент пары имя-значение ARLags указывает запаздывание, соответствующее несезонному коэффициенту AR, (« $1_{»).}$ SARLags определяет запаздывание, соответствующее сезонному коэффициенту AR, здесь при запаздывании 12. Несезонные и сезонные коэффициенты МА определяются аналогично. D определяет степень несезонного интегрирования. Seasonality определяет периодичность временного ряда, например, Seasonality = 12 - месячные данные. С тех пор Seasonality больше 0, степень сезонной интеграции $_{Ds}$ равна единице.

Всякий раз, когда вы включаете сезонные многочлены AR или MA (сигнализируемые заданием SAR или SMA) в спецификации модели, arima включает их в себя мультипликативно. arima устанавливает свойство P равно p + D + $_{ps}$ + s (здесь 1 + 1 + 12 + 12 = 26). Аналогично, arima устанавливает свойство Q равно q + $_{qs}$ (здесь 1 + 12 = 13).

Отображение значения SAR:

Mdl.SAR

ans=1×12 cell array
  Columns 1 through 8

    {[0]}    {[0]}    {[0]}    {[0]}    {[0]}    {[0]}    {[0]}    {[0]}

  Columns 9 through 12

    {[0]}    {[0]}    {[0]}    {[NaN]}

SAR массив ячеек возвращает 12 элементов, как указано SARLags. arima устанавливает коэффициенты с промежуточными лагами, равными нулю, для поддержания согласованности с индексацией массива ячеек MATLAB ®. Поэтому единственный ненулевой коэффициент соответствует запаздыванию 12 .

Все остальные свойства Mdl являются NaN- значение, указывающее, что соответствующие параметры модели могут быть оценены, или можно указать их значение с помощью точечной нотации.

Сезонная модель ARIMA с известными значениями параметров

Открыть сценарий в реальном времени

В этом примере показано, как определить мультипликативную сезонную модель ARIMA (для квартальных данных) с известными значениями параметров. Такую полностью заданную модель можно использовать в качестве входных данных для simulate или forecast.

Определение мультипликативной сезонной модели ARIMA

$(1-.5L) (1 + 0^{} . 7L4)^{(} 1-L)^{} 1_{(} 1-L4) ыт = (1^{+}_{} .3L$ ) (1-.2L4) αт,

где инновационное распределение является гауссовым с постоянной дисперсией 0,15. Здесь $(1-L)^{}$ 1 является оператором несезонной дифференциации и $(^{1-L4})$ является оператором сезонной дифференциации первой степени с периодичностью 4.

Mdl = arima('Constant',0,'AR',0.5,'D',1,'MA',0.3,...
    'Seasonality',4,'SAR',-0.7,'SARLags',4,...
    'SMA',-0.2,'SMALags',4,'Variance',0.15)

Mdl = 
  arima with properties:

     Description: "ARIMA(1,1,1) Model Seasonally Integrated with Seasonal AR(4) and MA(4) (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 10
               D: 1
               Q: 5
        Constant: 0
              AR: {0.5} at lag [1]
             SAR: {-0.7} at lag [4]
              MA: {0.3} at lag [1]
             SMA: {-0.2} at lag [4]
     Seasonality: 4
            Beta: [1×0]
        Variance: 0.15

Выходные данные определяют несезонные и сезонные коэффициенты AR с противоположными знаками по сравнению с многочленами запаздывания. Это согласуется с формой разностного уравнения модели. Выходные данные определяют задержки сезонных коэффициентов AR и MA с использованием SARLags и SMALagsсоответственно. D определяет степень несезонного интегрирования. Seasonality = 4 определяет квартальные данные с одной степенью сезонной интеграции.

Указаны все значения параметров, то есть свойство объекта отсутствует NaN-значение.

Укажите мультипликативную модель ARIMA с помощью приложения эконометрического моделирования

В приложении Econometric Modeler можно указать структуру запаздывания, наличие константы и инновационное распределение модели SARIMA (p, D, q) × ₍ps_, _Ds, qs) s, выполнив следующие шаги. Все указанные коэффициенты неизвестны, но поддаются оценке.

В командной строке откройте приложение Econometric Modeler.
```
econometricModeler
```
Можно также открыть приложение из галереи приложений (см. Econometric Modeler).
На панели Временной ряд (Time Series) выберите временной ряд ответа, по которому будет соответствовать модель.
На вкладке Эконометрический моделирующий (Econometric Modeler) в разделе Модели (Models) щелкните стрелку, чтобы отобразить галерею моделей.
В разделе Модели ARMA/ARIMA галереи нажмите SARIMA. Сведения о создании моделей SARIMAX см. в разделе Спецификации моделей ARIMAX.
Появится диалоговое окно Параметры модели SARIMA (SARIMA Model Parameters
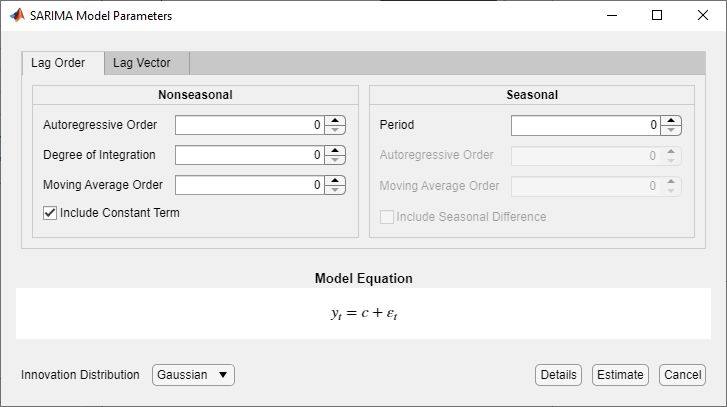
Укажите структуру запаздывания. На вкладке «Порядок запаздывания» можно задать модель SARIMA (p, D, q) × ₍ps_, _Ds, qs) s, включающую:
- Все последовательные задержки от 1 через их соответствующие порядки, в несезонных многочленов
- Задержки, все из которых являются последовательными кратными периодам, в сезонных многочленах
- Сезонный полином интегрирования s-степени
Используйте вкладку Вектор запаздывания (Lag Vector), чтобы задать определенные задержки для всех полиномов. Дополнительные сведения см. в разделе Интерактивное определение многочленов оператора задержки. Независимо от используемой вкладки можно проверить форму модели, проверив уравнение в разделе «Уравнение модели».

Например, рассмотрим модель SARIMA (2,1,1) × (_2,1,1) 12.

$(1 -_{} {ϕ1L}_{} -^{} ϕ2L2)_{(} 1^{−}_{}^{Φ12L12} - Φ24L24)^{(} 1_{-} L) (1_{−} L12)_{yt}^{=} c_{+}$ (1 + θ1L) (1 + Θ12L12) αt,

где _αt - серия гауссовых инноваций IID.

Модель включает все последовательные AR и MA с интервалом от 1 до их соответствующих заказов. Кроме того, запаздывания многочленов SAR и SMA являются последовательными кратными периоду от 12 до их соответствующего заданного порядка, умноженного на 12. Поэтому используйте вкладку Порядок задержки (Lag Order), чтобы указать модель.

В несезонном разделе:
1. Установить степень интеграции как 1.
2. Задать авторегрессионный порядок как 2.
3. Задайте для заказа скользящего среднего значение 1.
В разделе Сезонные:
1. Установить период в 12.
2. Задать авторегрессионный порядок как 2. Этот ввод определяет включение интервалов 12 и 24 SAR (то есть первого и второго кратных значению периода).
3. Задайте для заказа скользящего среднего значение 1. Этот ввод определяет включение задержки 12 SMA (то есть первого кратного значения Period).
4. Установите флажок Включить сезонную разницу.
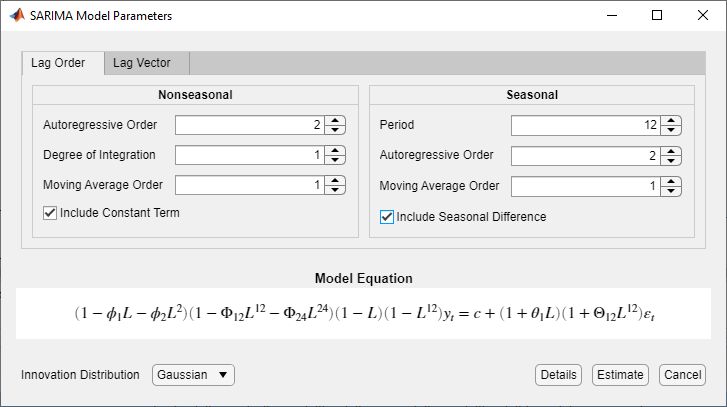
Убедитесь, что уравнение в разделе «Уравнение модели» соответствует модели.

Чтобы исключить константу из модели и указать, что нововведения являются гауссовыми, выполните предыдущие шаги и снимите флажок Включить условие константы (Include Constant Term).
Чтобы указать t-распределенные инновации, выполните предыдущие шаги и нажмите кнопку Innovation Distribution, а затем выберите t.

В качестве другого примера рассмотрим модель SARIMA (12,1,1) × (_2,1,1) 12.

$(1 -_{} {ϕ1L}_{−}^{} ϕ12L12)_{(} 1^{−} Φ24L24) (^{1} -_{L}) (1 -_{} L12) {yt}_{=}^{c} +_{(} 1$ + θ1L) (1 + Θ12L12) αt.

Модель не включает последовательные задержки AR, и задержки полинома SAR не являются последовательными кратными периоду. Поэтому используйте вкладку Вектор запаздывания (Lag Vector), чтобы указать эту модель:

В диалоговом окне «Параметры модели SARIMA» перейдите на вкладку «Вектор задержки».
В несезонном разделе:
1. Установить степень интеграции как 1.
2. Установить авторегрессионные задержки в значение 1 12.
3. Установить задержки скользящего среднего в 1.
В разделе Сезонные:
1. Установить сезонность как 12. Приложение включает 12-градусный полином сезонной интеграции.
2. Установить авторегрессионные задержки в значение 24. Этот вход определяет включение задержки 24 SAR. Входные данные не зависят от значения в поле Сезонность.
3. Установить задержки скользящего среднего в 12. Этот ввод определяет включение задержки 12 SMA. Входные данные не зависят от значения в поле Сезонность.
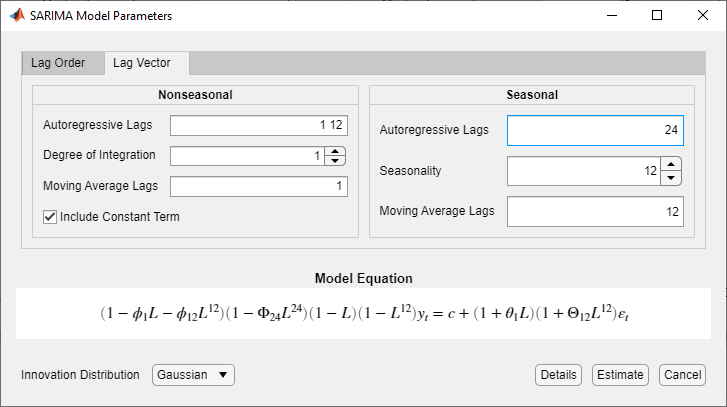
Убедитесь, что уравнение в разделе «Уравнение модели» соответствует модели.

После задания модели щелкните Оценка (Estimate), чтобы оценить все неизвестные параметры в модели.

Документация