Оцените и проверьте нелинейные модели на основе данных с одним входом/одним выходом (SISO), чтобы найти модель, которая лучше всего отражает динамику системы.
После завершения этого учебного пособия вы сможете выполнить следующие задачи с помощью приложения «Идентификация системы»:
Импорт объектов данных из рабочей области MATLAB ® в приложение.
Оценка и проверка нелинейных моделей на основе данных.
Постройте график и проанализируйте поведение нелинейностей.
В данном учебном пособии используется файл данных twotankdata.mat, который содержит данные временной области SISO для двухбачковой системы, показанной на следующем рисунке.
Двухбачковая система
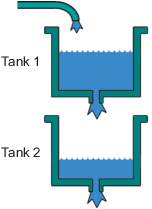
В двухбачковой системе вода переливается по трубопроводу в резервуар 1, сливается в резервуар 2 и выходит из системы через небольшое отверстие в нижней части резервуара 2. Измеренным входом u (t) в систему является напряжение, подаваемое на насос, который подает воду в бак 1 (в вольтах). Измеренный выходной сигнал y (t) - высота воды в нижнем резервуаре (в метрах).
Основываясь на законе Бернулли, который гласит, что вода, протекающая через небольшое отверстие на дне резервуара, нелинейно зависит от уровня воды в резервуаре, вы ожидаете, что взаимосвязь между входными и выходными данными будет нелинейной.
twotankdata.mat включает 3000 образцов с временем выборки 0,2 с.
Нелинейные дискретно-временные модели черного ящика можно оценить как для данных с одним выходом, так и для данных с несколькими выходами во временной области. Можно выбрать один из двух типов нелинейных структур модели черного ящика:
Нелинейные модели ARX
Модели Хаммерстайн-Винер
Примечание
Модели черного ящика Hammerstein-Wiener можно оценить только по данным ввода/вывода. Эти модели не поддерживают данные временных рядов, где отсутствуют входные данные.
Дополнительные сведения об оценке нелинейных моделей черного ящика см. в разделе Идентификация нелинейных моделей.
Нелинейная модель ARX состоит из регрессоров модели и выходной функции. Функция вывода включает в себя линейные и нелинейные функции, которые действуют на регрессоры модели для получения выходного сигнала модели и фиксированного смещения для этого выходного сигнала. Эта блок-схема представляет структуру нелинейной модели ARX в сценарии моделирования.
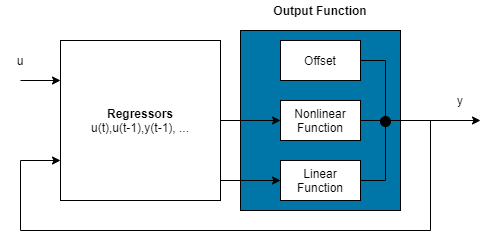
Программное обеспечение вычисляет выход нелинейной модели ARX y в два этапа:
Он вычисляет значения регрессора из текущих и прошлых входных значений и прошлых выходных данных.
В простейшем случае регрессоры представляют собой запаздывающие входы и выходы, такие как u (t-1) и y (t-3). Такие регрессоры называются линейными регрессорами. Линейные регрессоры задаются с помощью linearRegressor объект. Можно также задать линейные регрессоры, используя линейные порядки моделей ARX в качестве входного аргумента. Дополнительные сведения см. в разделе Нелинейные заказы модели ARX и задержка. Однако этот второй подход ограничивает набор регрессоров линейными регрессорами с последовательными задержками. Для создания полиномиальных регрессоров используйте polynomialRegressor объект. Можно также указать пользовательские регрессоры, которые являются нелинейными функциями отложенных входов и выходов. Например, u (t-1) y (t-3) является пользовательским регрессором, который умножает экземпляры ввода и вывода вместе. Укажите пользовательские регрессоры с помощью customRegressor объект.
Можно назначить любой из регрессоров в качестве входных данных линейному функциональному блоку выходной функции, нелинейному функциональному блоку или и тому и другому.
Он отображает регрессоры на выходные данные модели с помощью функционального блока вывода. Выходной функциональный блок может включать в себя линейные и нелинейные блоки параллельно. Например, рассмотрим следующее уравнение:
Q (x − r)) + d
Здесь x - вектор регрессоров, а r - среднее значение x. r) + y0 - выход линейного функционального (x − r)) + y0 представляет выход нелинейного функционального блока. Q - это проекционная матрица, которая делает вычисления хорошо обусловленными. d - скалярное смещение, которое добавляется к объединенным выходам линейного и нелинейного блоков. Точная форма F (x) зависит от выбора функции вывода. Можно выбрать из доступных объектов отображения, таких как сети с древовидными разделами, вейвлет-сети и многослойные нейронные сети. Можно также исключить линейный или нелинейный функциональный блок из функции вывода.
При оценке нелинейной модели ARX программное обеспечение вычисляет значения параметров модели, такие как L, r, d, Q, и другие параметры, определяющие g.
Результирующими нелинейными моделями ARX являются idnlarx объекты, хранящие все данные модели, включая регрессоры модели и параметры выходной функции. Дополнительные сведения об этих объектах см. в разделе Нелинейные структуры модели.
Эта блок-схема представляет структуру модели Хаммерштейна-Винера:

Где,
f - нелинейная функция, которая преобразует входные данные u (t) как w (t) = f (u (t)).
w (t), внутренняя переменная, является выходом блока входной нелинейности и имеет тот же размер, что и u (t).
B/F - линейная передаточная функция, которая преобразует w (t) как x (t) = (B/F) w (t).
x (t), внутренняя переменная, является выходом линейного блока и имеет тот же размер, что и y (t).
B и F аналогичны многочленам в линейной модели ошибки вывода. Дополнительные сведения о моделях выходных ошибок см. в разделе Что такое модели полиномов?.
Для ny выходов и nu входов линейный блок является матрицей передаточной функции, содержащей записи:
i (q)
где j = 1,2,...,ny и i = 1,2,...,nu.
h - нелинейная функция, которая отображает выходной сигнал линейного блока x (t) в выходной сигнал системы y (t) как y (t) = h (x (t)).
Поскольку f действует на входной порт линейного блока, эта функция называется входной нелинейностью. Аналогично, поскольку h действует на выходной порт линейного блока, эта функция называется выходной нелинейностью. Если система содержит несколько входов и выходов, необходимо определить функции f и h для каждого входного и выходного сигнала. Нет необходимости включать в структуру модели как входную, так и выходную нелинейность. Когда модель содержит только входную нелинейность f, она называется моделью Хаммерштейна. Аналогично, когда модель содержит только выходную нелинейность h, она называется моделью Винера.
Программное обеспечение вычисляет выходной сигнал модели Хаммерштейна-Винера y в три этапа:
Вычислите w (t) = f (u (t)) из входных данных.
w (t) является входом в линейную передаточную функцию B/F.
Входная нелинейность является статической (незамеченной) функцией, где значение выходного сигнала в заданное время t зависит только от входного значения в момент времени t.
Можно настроить нелинейность ввода как сигмоидальную сеть, вейвлет-сеть, насыщенность, мертвую зону, кусочно-линейную функцию, одномерный многочлен или пользовательскую сеть. Можно также удалить входную нелинейность.
Вычислите выходной сигнал линейного блока, используя w (t) и исходные условия: x (t) = (B/F) w (t).
Линейный блок можно настроить, задав порядки числителя B и знаменателя F.
Вычислите выходной сигнал модели путем преобразования выходного сигнала линейного блока x (t) с использованием нелинейной функции h как y (t) = h (x (t)).
Аналогично входной нелинейности, выходная нелинейность является статической функцией. Нелинейность вывода можно настроить так же, как нелинейность ввода. Можно также удалить нелинейность вывода, так что y (t) = x (t).
Результирующими моделями являются idnlhw объекты, хранящие все данные модели, включая параметры модели и оценщики нелинейности. Дополнительные сведения об этих объектах см. в разделе Нелинейные структуры модели.
Загрузить данные образца в twotankdata.mat путем ввода следующей команды в окне команд MATLAB:
load twotankdata
Эта команда загружает следующие две переменные в обозреватель рабочей области MATLAB:
u - входные данные, которые представляют собой напряжение, подаваемое на насос, который подает воду в резервуар 1 (в вольтах).
y - выходные данные, которые представляют собой высоту воды в резервуаре 2 (в метрах).
Объекты данных Toolbox™ System Identification инкапсулируют как значения данных, так и свойства данных в один объект. Для удобного управления этими объектами данных как отдельными объектами можно использовать команды панели инструментов идентификации системы.
Образцы данных должны быть уже загружены в рабочую область MATLAB, как описано в разделе Загрузка данных в рабочую область MATLAB.
Используйте следующие команды для создания двух iddata объекты данных, ze и zv, где ze содержит данные для оценки модели и zv содержит данные для проверки модели. Ts - время выборки.
Ts = 0.2; % Sample time is 0.2 sec z = iddata(y,u,Ts); % First 1000 samples used for estimation ze = z(1:1000); % Remaining samples used for validation zv = z(1001:3000);
Просмотр свойств iddata объект, используйте get команда. Например:
get(ze)
Программное обеспечение MATLAB возвращает следующие свойства и значения данных:
Domain: 'Time'
Name: ''
OutputData: [1000x1 double]
y: 'Same as OutputData'
OutputName: {'y1'}
OutputUnit: {''}
InputData: [1000x1 double]
u: 'Same as InputData'
InputName: {'u1'}
InputUnit: {''}
Period: Inf
InterSample: 'zoh'
Ts: 0.2000
Tstart: 0.2000
SamplingInstants: [1000x0 double]
TimeUnit: 'seconds'
ExperimentName: 'Exp1'
Notes: {}
UserData: []Для изменения свойств данных используйте точечное представление. Например, чтобы назначить имена каналов и единицы измерения, маркирующие оси печати, введите следующий синтаксис в окне команд MATLAB:
% Set time units to minutes ze.TimeUnit = 'sec'; % Set names of input channels ze.InputName = 'Voltage'; % Set units for input variables ze.InputUnit = 'V'; % Set name of output channel ze.OutputName = 'Height'; % Set unit of output channel ze.OutputUnit = 'm'; % Set validation data properties zv.TimeUnit = 'sec'; zv.InputName = 'Voltage'; zv.InputUnit = 'V'; zv.OutputName = 'Height'; zv.OutputUnit = 'm';
Чтобы проверить, что InputName имущество ze при изменении введите следующую команду:
ze.inputname
Совет
Имена свойств, например InputName, не чувствительны к регистру. Можно также сокращать имена свойств, которые начинаются с Input или Output путем замены u для Input и y для Output в имени свойства. Например, OutputUnit эквивалентно yunit.
Чтобы открыть приложение System Identification, введите следующую команду в окне MATLAB Command Window:
systemIdentification
Имя сеанса по умолчанию, Untitled, отображается в строке заголовка.
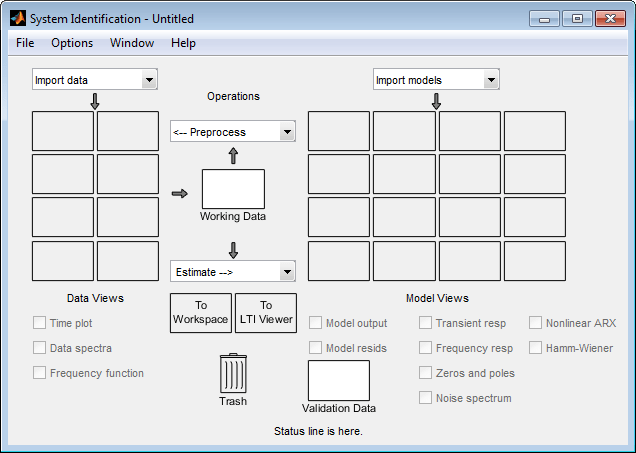
Объекты данных можно импортировать в приложение из рабочей области MATLAB.
Необходимо создать объекты данных, как описано в разделе Создание объектов iddata, и открыть приложение, как описано в разделе Запуск приложения идентификации системы.
Для импорта объектов данных:
В приложении Идентификация системы выберите Импорт данных > Объект данных.
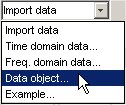
Это действие открывает диалоговое окно Импорт данных (Import Data).
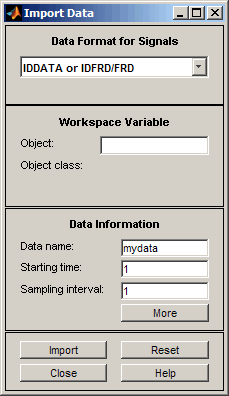
Войти ze в поле Объект для импорта оценочных данных. Нажмите Enter.
Это действие вводит информацию об объекте в поля Импорт данных.
Нажмите кнопку «» Дополнительно «», чтобы просмотреть дополнительные сведения об этих данных, включая имена каналов и единицы измерения.
Щелкните Импорт (Import), чтобы добавить значок с именем ze в приложение «Идентификация системы».
В диалоговом окне «Импорт данных» введите zv в поле Объект для импорта данных проверки. Нажмите Enter.
Щелкните Импорт (Import), чтобы добавить значок с именем zv в приложение «Идентификация системы».
В диалоговом окне «Импорт данных» нажмите кнопку «Закрыть».
В приложении «Идентификация системы» перетащите значок zv данных проверки в прямоугольник «Данные проверки». Значок ze данных оценки уже обозначен в прямоугольнике рабочих данных.
Либо щелкните правой кнопкой мыши значок zv , чтобы открыть диалоговое окно Информация о данных/модели (Data/model Info). Установите флажок Использовать как данные проверки. Нажмите кнопку Применить, а затем Закрыть, чтобы добавить zv в прямоугольник «Данные проверки».
Приложение «Идентификация системы» теперь напоминает следующий рисунок.
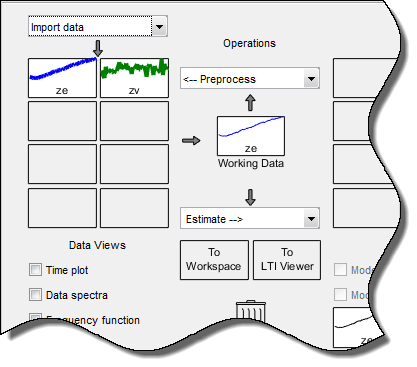
В этой части учебного пособия выполняется оценка нелинейной модели ARX с использованием стандартной структуры модели и опций оценки.
Данные должны быть уже подготовлены, как описано в разделе Подготовка данных. Дополнительные сведения о нелинейных моделях ARX см. в разделе Что такое нелинейная модель ARX?.
Примечание
Иллюстрации в этом учебном пособии представляют типичный сеанс приложения «Идентификация системы». Результаты могут не совпадать с результатами на изображениях.
В приложении Идентификация системы выберите Оценка > Нелинейные модели.
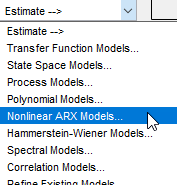
Это действие открывает диалоговое окно Оценить нелинейные модели ARX (Estimate Nonlinear ARX Models).
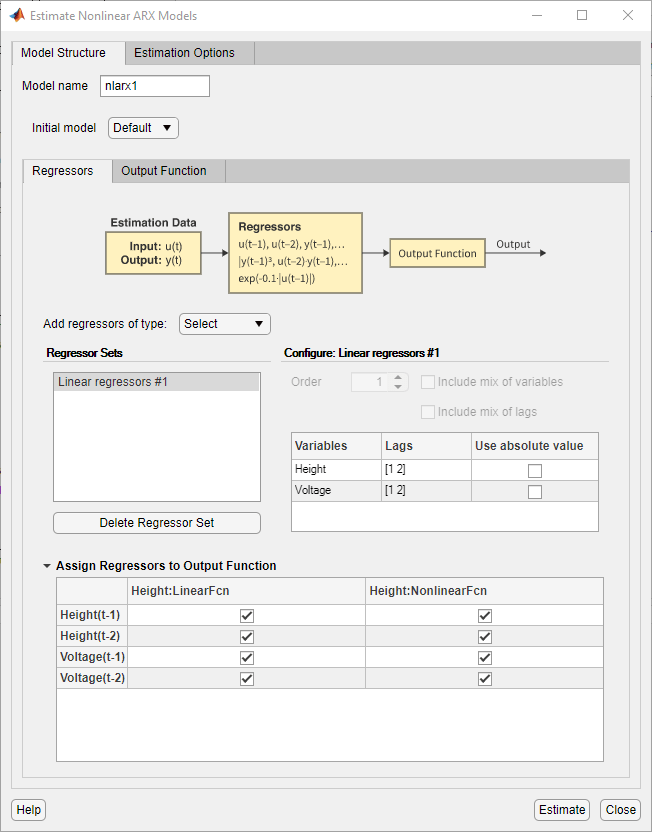
Диалоговое окно содержит две вкладки - «Структура модели» и «Параметры оценки».
Вкладка Структура модели (Model Structure) содержит параметры, которые настраивают структуру модели, такие как выбор регрессоров и тип выходной функции. Укажите имя модели для оценки в поле Имя модели (Model name). Имя модели по умолчанию: nlarx1.
Используйте вкладку Регрессоры (Regressors), чтобы создать наборы регрессоров для использования. По умолчанию приложение создает набор линейных регрессоров с лагами [1 2] в каждой переменной и сохраняет регрессор как Linear regressors #1 в области «Наборы регрессоров». Эта панель содержит таблицу, которая позволяет изменять задержки, используемые для каждой переменной.
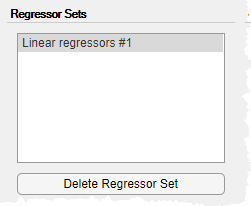
Панель конфигурации Configure: Linear regressors # 1 содержит таблицу, в которой показаны значения задержки, используемые набором регрессоров. Эти задержки можно изменить .
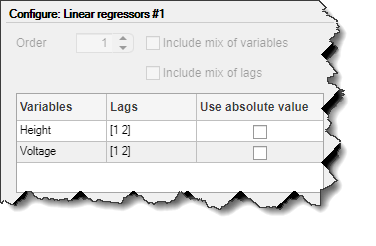
В таблице назначения регрессоров Assign Regressors to Output Function перечислены имена регрессоров и назначения регрессоров компонентам выходных функций.
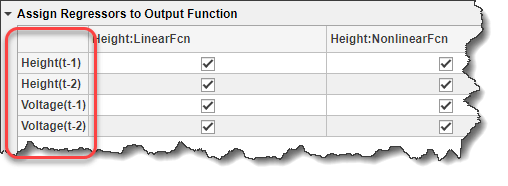
Назначения регрессоров в таблице создают модель для вывода Height из:
Высота (t) = f (высота (t-1), высота (t-2), напряжение (t-1), напряжение (t-2))
Здесь f (.) - статическая нелинейная функция, отображающая регрессоры на выход. Чтобы выбрать f (.) и связанные с ним параметры, используйте закладку Функция вывода.
Можно добавить дополнительные наборы регрессоров, такие как полиномы и пользовательские формулы, выбрав тип регрессора в разделе Добавить регрессоры типа.
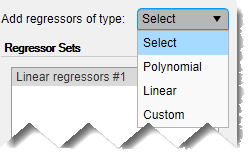
В этом примере используется только Linear regressors #1.
Выберите закладку Output Function (Функция вывода).
На вкладке показано, что приложение выбирает Wavelet Network в качестве типа по умолчанию функции вывода f (.). Эта функция использует сумму линейной функции, нелинейную функцию (которая является суммой масштабированных вейвлетов) и член смещения для вычисления выходного сигнала. На вкладке также показан набор параметров конфигурации. Количество вейвлетов, используемых функцией, конфигурируется для автоматического выбора во время оценки. Этот выбор можно изменить. Можно также изменить начальные значения линейных коэффициентов и смещения. Для первой оценки сохраните варианты по умолчанию.
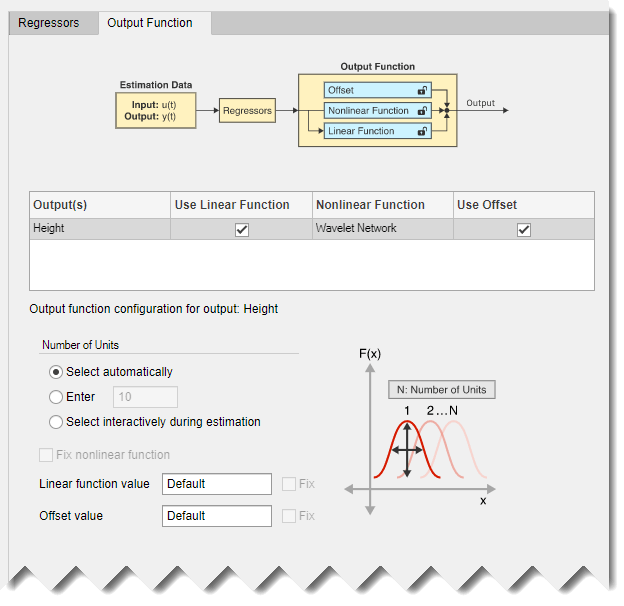
Щелкните Оценка (Estimate).
Это действие добавляет модель nlarx1 на плату модели приложения System Identification, как показано на следующем рисунке.
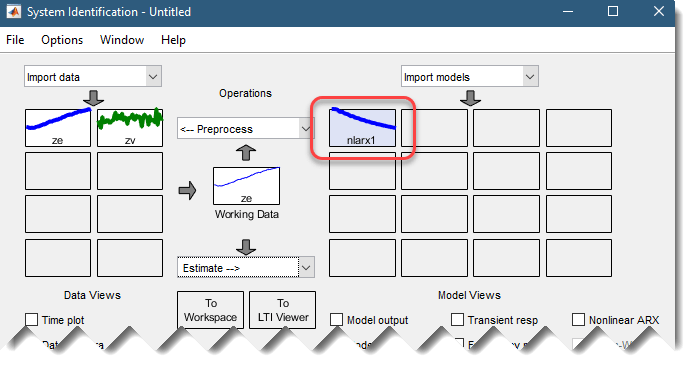
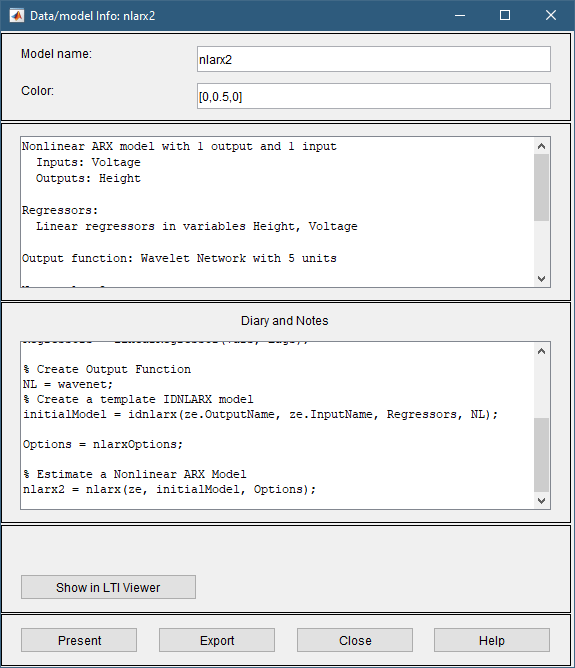
Дважды щелкните или щелкните правой кнопкой мыши значок модели. nlarx1 На плате модели отображается информация о расчетной модели. Верхняя область описывает структуру модели и результаты оценки (используемые данные, процент соответствия и другие показатели качества). В нижней области (Дневник и Заметки) отображается сценарий MATLAB, который можно использовать для воспроизведения результатов оценки в командной строке.
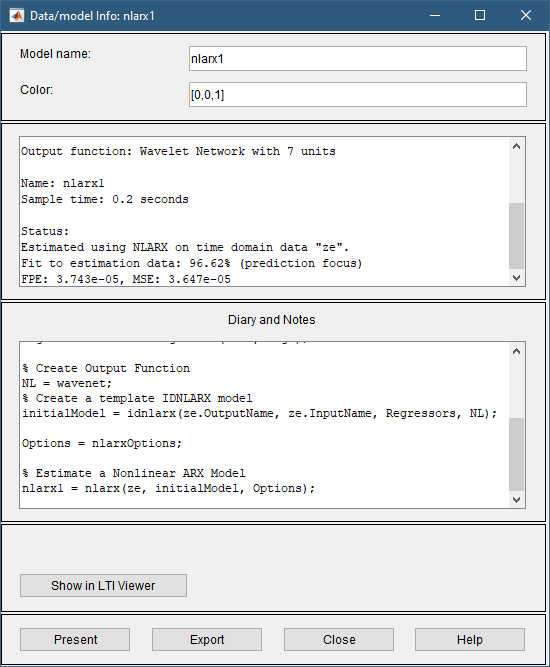
Примечание
Fit (%) вычисляется с использованием набора оценочных данных с фокусом прогнозирования. а не набор данных проверки. Однако график вывода модели на следующем шаге сравнивает аппроксимацию с набором данных проверки. Чтобы увидеть, насколько хорошо модель может моделировать отклик независимого набора данных проверки, используйте график Вывод модели (Model Output), как описано на следующем шаге.
В области Представления модели приложения Идентификация системы выберите Вывод модели. Это действие моделирует модель с использованием входных данных проверки в качестве входных данных модели и строит график смоделированных выходных данных поверх выходных данных проверки.
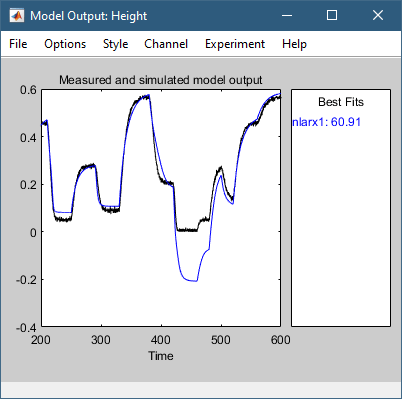
Область «Наилучшие посадки» графика вывода модели показывает согласие между выводом модели и выводом данных проверки с использованием нормализованной среднеквадратичной (NRMSE) метрики качества соответствия. Соглашение плохо в 400-500 временных промежутках.
Выполните следующую процедуру для просмотра формы нелинейности как функции регрессоров на графике нелинейной модели ARX.
В приложении Идентификация системы установите флажок Нелинейный ARX для просмотра сечений нелинейности.
По умолчанию график показывает взаимосвязь между выходными регрессорами Height(t-1) и Height(t-2). На этом графике показана обычная плоскость на следующем рисунке. Таким образом, соотношение между регрессорами и выходным сигналом является приблизительно линейной плоскостью.
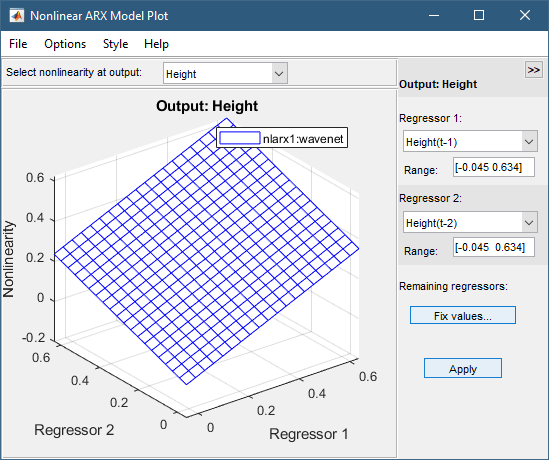
В окне График нелинейной модели ARX (Nonlinear ARX Model Plot) установите для параметра Регрессор 1 значение Voltage(t-1). Установите для регрессора 2 значение Voltage(t-2). Нажмите кнопку «Применить».
Отношение между этими регрессорами и выводом нелинейно, как показано на следующем графике.
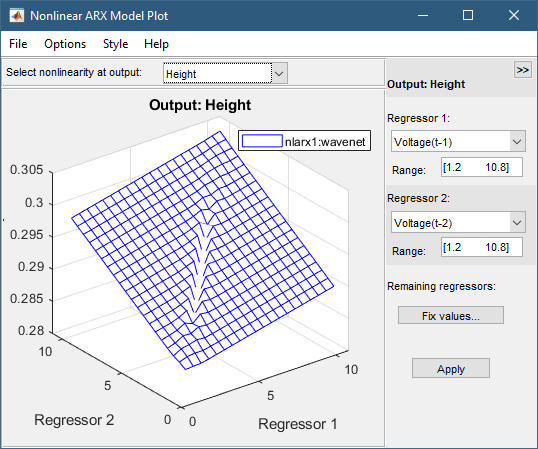
Чтобы повернуть нелинейную поверхность, выберите «Стиль» > «Повернуть» 3D а затем перетащите график в новую ориентацию.
Для отображения 1-D сечения для Регрессора 1 установите для Регрессора 2 значение noneи нажмите кнопку «Применить». На следующем рисунке показана результирующая величина нелинейности для Регрессора 1, которая представляет сдвинутый по времени сигнал напряжения, Voltage(t-1).
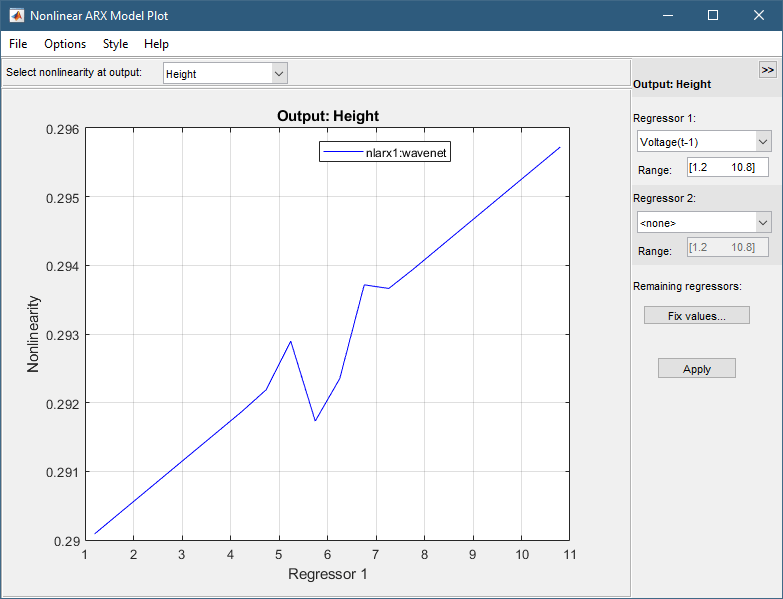
В этой части учебного пособия оценивается нелинейная модель ARX с определенными параметрами задержки ввода и нелинейности. Обычно заказы моделей выбираются методом проб и ошибок до тех пор, пока не будет получена модель, обеспечивающая точное соответствие данным.
Необходимо уже оценить нелинейную модель ARX с настройками по умолчанию, как описано в разделе Оценка нелинейной модели ARX с настройками по умолчанию.
В диалоговом окне Оценить нелинейные модели ARX (Estimate Nonlinear ARX Models) выберите вкладку Структура модели (Model Structure), а затем вкладку Регрессоры (Regessors).
На панели «Configure: Linear Regressors # 1» измените значениеVoltage задержки переменных до [3 4]. Это происходит потому, что данные свидетельствуют о том, что между входом и выходом имеется минимум 3 пробных запаздывания.
Это действие обновляет список регрессоров для отображения Voltage(t-3) и Voltage(t-4)- сроки с минимальной задержкой в три образца.
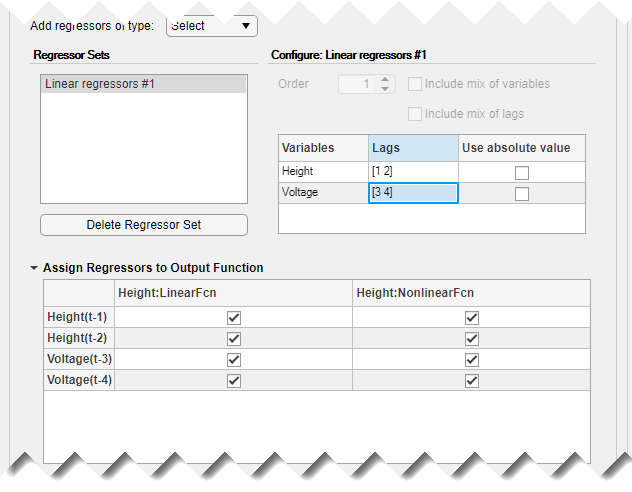
Щелкните Оценка (Estimate).
Это действие добавляет модель nlarx2 в приложение Идентификация системы (System Identification) и обновляет окно Вывод модели (Model Output), чтобы включить эту модель. Дважды щелкните по nlarx2 на панели модели главного окна приложения отображаются результаты оценки.
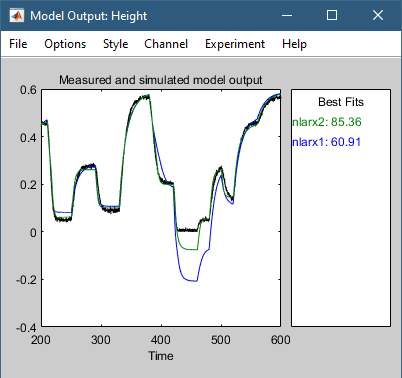
Приложение также обновляет выходной график модели для отображения соответствия модели nlarx2 в набор данных проверки zv. График показывает, что выбор правильных интервалов входных переменных улучшает аппроксимацию.
В диалоговом окне Оценить нелинейные модели ARX (Estimate Nonlinear ARX Models) выберите вкладку Структура модели (Model Structure), а затем вкладку Регрессоры (Regessors).
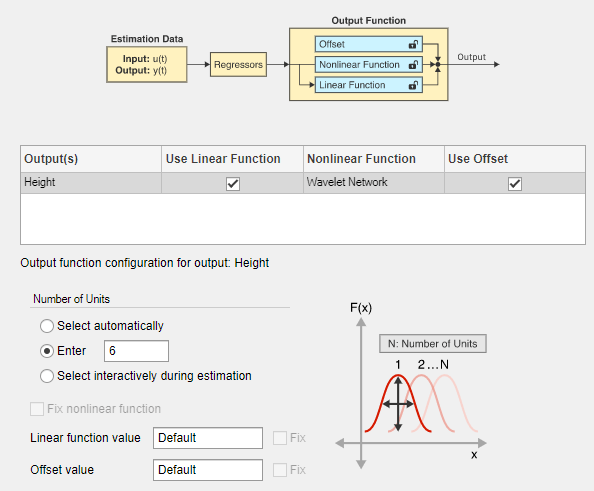
Выберите закладку Output Function (Функция вывода).
В поле «Количество единиц» выберите «Enter» и введите 6. Установка определенного числа управляет гибкостью нелинейной функции путем непосредственного указания количества вейвлетов, используемых вейвлет-сетью.
Щелкните Оценка (Estimate).
Это действие добавляет модель nlarx3 в приложении System Identification (Идентификация системы). Также обновляется окно Model Output (Вывод модели), как показано на следующем рисунке.
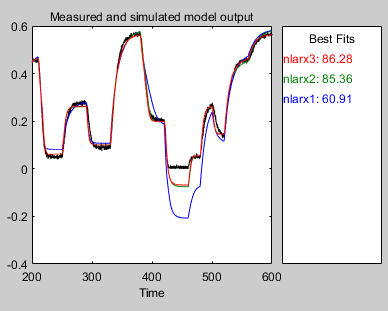
Можно оценить нелинейную модель ARX, которая использует более высокие степени запаздывающих переменных в качестве регрессоров. В этом примере добавляются многочлены второго порядка запаздывающих переменных, включая перекрестные члены.
В диалоговом окне «Оценка нелинейных моделей ARX» перейдите на вкладку «Структура модели», а затем на вкладку «Регрессоры».
Разверните узел Добавить регрессоры типа (Add regressors of type) и выберите Полином (Polynomial).
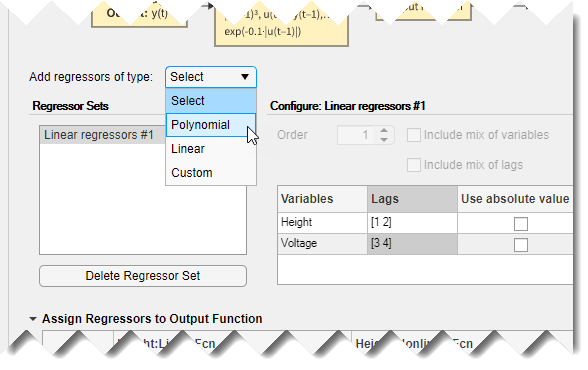
Это действие добавляет набор полиномиальных регрессоров с именем Polynomial regressors #1 в список наборов регрессоров. По умолчанию этот аппарат настроен на генерацию регрессоров порядка 2, как показано на панели конфигурации.
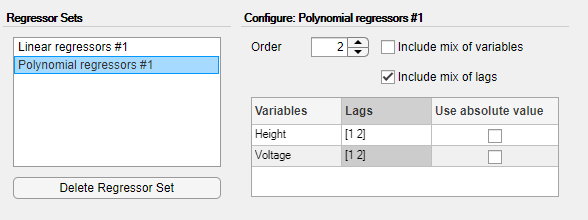
Изменить Voltage отстает до [3 4].
Выберите Включить сочетание переменных, чтобы включить все перекрестные термины. Это действие добавляет десять регрессоров второго порядка к модели в дополнение к четырем, внесенным линейным регрессором № 1.
Щелкните Оценка (Estimate). Это действие добавляет модель nlarx4 app. Приложение обновляет график вывода модели, как показано на следующем рисунке.
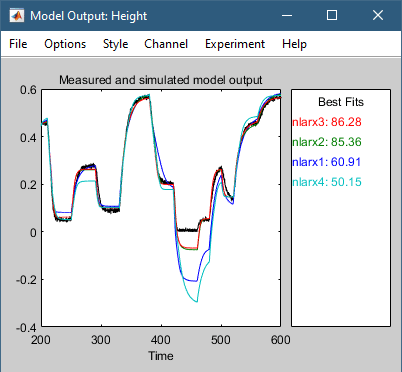
График показывает, что добавление полиномиальных регрессоров не улучшило обобщающую способность модели. То есть модель не обеспечивает лучшего соответствия между выводом модели и измеренным выводом для независимых данных проверки. Этот результат обычно является сценарием с перегонками, то есть когда модель содержит больше регрессоров, чем абсолютно необходимо.
Можно оценить нелинейную модель ARX, которая включает только подмножество регрессоров, которые вводятся в нелинейный блок в качестве входных данных. По умолчанию в нелинейном блоке используются все регрессоры. В этой части учебного пособия нелинейному блоку назначается только подмножество регрессоров.
Необходимо уже указать структуру модели, как описано в разделе Изменение нелинейной структуры модели ARX.
В диалоговом окне Оценить нелинейные модели ARX (Estimate Nonlinear ARX Models) выберите вкладку Структура модели (Model Structure), а затем вкладку Регрессоры (Regessors).
При сворачивании разверните панель «Назначение регрессоров функции вывода».
Снимите флажки для всех регрессоров второго порядка в столбце Height: NonlinearFcn таблицы. Кроме того, снимите флажки для всех регрессоров с перекрестными терминами (то есть регрессоров, состоящих из продуктов из 2 терминов) из Height: LinearFcn
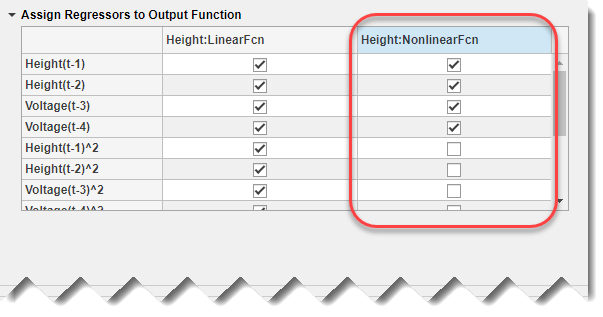
Щелкните Оценка (Estimate).
Это действие добавляет модель nlarx5 в приложении Идентификация системы (System Identification). Также обновляется окно Вывод модели (Model Output).
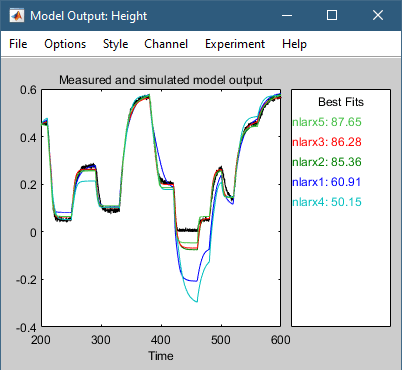
Эта модель показывает улучшенную способность к обобщению.
Можно оценить ряд нелинейных моделей ARX, внося систематические изменения в структуру модели и основывая каждую новую модель на конфигурации ранее оцененной модели. В этой части учебного пособия оценивается нелинейная модель ARX, аналогичная существующей модели (nlarx3), но которая имеет другую нелинейность в выходной функции.
В диалоговом окне Оценить нелинейные модели ARX (Estimate Nonlinear ARX Models) выберите вкладку Структура модели (Model Structure).
Выбрать nlarx3 из начальной модели. При этом свойства, отображаемые на вкладках Регрессоры (Regressors) и Функция вывода (Output Function), устанавливаются в значения, соответствующие nlarx3.
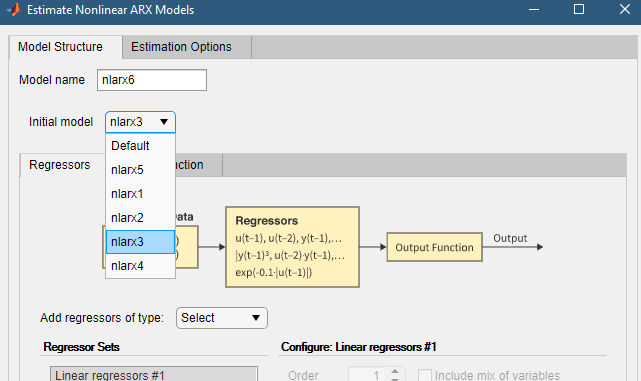
Выберите закладку Output Function (Функция вывода).
В таблице измените выбор нелинейной функции на Sigmoid Network. При этом функция вывода устанавливается в сигмоидальную сеть.
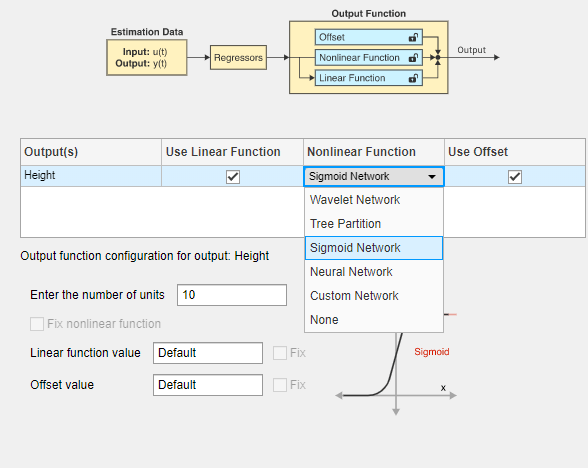
В поле «Введите количество единиц» введите 6.
Щелкните Оценка (Estimate).
Это действие добавляет модель nlarx6 в приложении «Идентификация системы» (System Identification app.). Также обновляется график «Вывод модели» (Model Output), как показано на следующем рисунке.
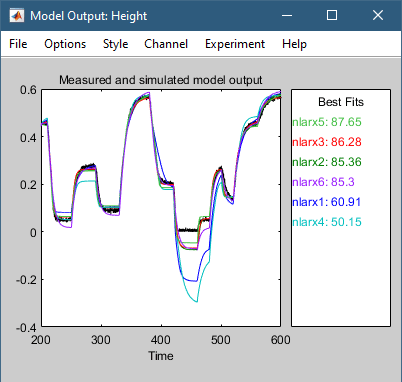
Лучшая модель - это простейшая модель, которая точно описывает динамику. Результаты показывают, что модель nlarx3 является кандидатом на то, чтобы быть лучшей моделью idnlarx для этих данных, основываясь на различных вариантах структуры модели, которые исследовал этот пример.
Перетащите элемент nlarx3 в поле Кому в рабочую область (To Workspace) в главном окне приложения Идентификация системы (System Identification). Либо дважды щелкните значок nlarx3 для открытия информационной доски. Затем щелкните Экспорт (Export), чтобы экспортировать модель в основное рабочее пространство.
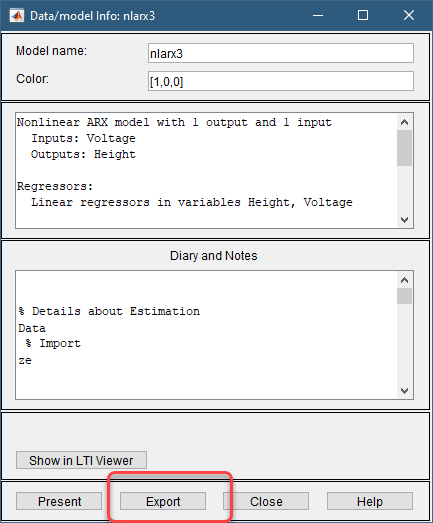
В этой части учебного пособия выполняется оценка нелинейных моделей Хаммерстайна-Винера с использованием стандартной структуры модели и опций оценки.
Данные должны быть уже подготовлены, как описано в разделе Подготовка данных. Дополнительные сведения о нелинейных моделях ARX см. в разделе Что такое модель Хаммерштейна-Винера?
Примечание
Иллюстрации в этом учебном пособии представляют типичный сеанс приложения «Идентификация системы». Результаты могут не совпадать с результатами на изображениях.
В приложении «Идентификация системы» выберите «Оценка» > «Модели Хаммерштейна-Винера», чтобы открыть диалоговое окно «Оценка моделей Хаммерштейна-Винера». Диалоговое окно содержит две вкладки - «Структура модели» и «Параметры оценки».
Проверьте структуру модели по умолчанию. Вкладка Структура модели (Model Structure) содержит три вкладки, по одной для каждого компонента модели. Этими компонентами являются входная нелинейность, линейный динамический блок и выходная нелинейность.
Выберите вкладку Input Nonlinearity (Нелинейность ввода). Нелинейность по умолчанию - это функция Кусочно-линейная с 10 точками останова.
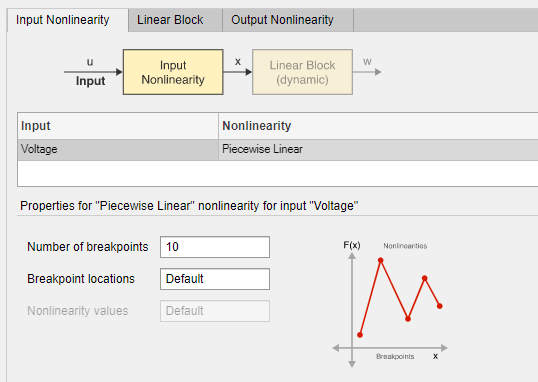
Выберите вкладку «Линейный блок». Линейная передаточная функция имеет порядок числителей 2, что подразумевает многочлен второго порядка в z-1, порядок знаменателей 3 и задержку на входе 1 выборка.
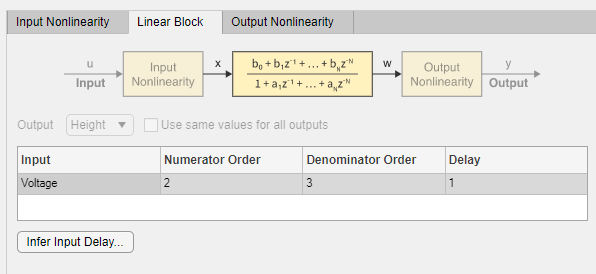
Выберите вкладку Вывод нелинейности (Output Nonlinearity). Как и на вкладке Входная нелинейность (Input Nonlinearity), нелинейностью по умолчанию является функция Кусочно-линейная (Piecewise Linear) с 10 точками останова.
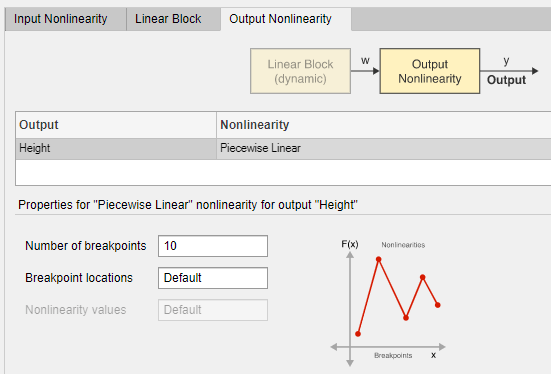
Щелкните Оценка (Estimate).
Это действие оценивает параметры модели Хаммерштейна-Винера, чтобы минимизировать разницу между выходом модели и измеренным выходом (ze.OutputData). Оценочные параметры:
Местоположения точек останова (координаты x и y) входных и выходных кусочно-линейных функций.
Числитель и многочленовые коэффициенты знаменателя, составляющие линейную блочную передаточную функцию.
Программа добавляет расчетную модель nlhw1 на плату модели приложения System Identification.
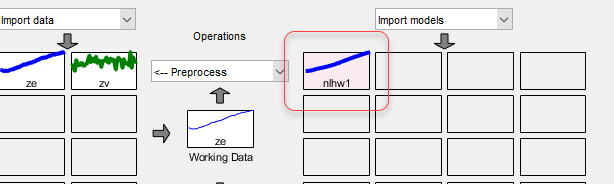
В приложении Идентификация системы установите флажок Вывод модели.
Это действие моделирует модель с использованием входных данных проверки в качестве входных данных модели и строит график смоделированных выходных данных поверх выходных данных проверки. Обратите внимание, что для данных проверки установлено значение zv.
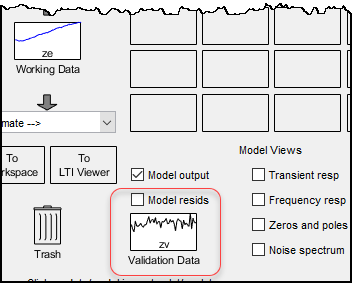
В области Наилучшие посадки (Best Fits) окна Вывод модели (Model Output) показано согласие между выводом модели и выводом данных проверки.
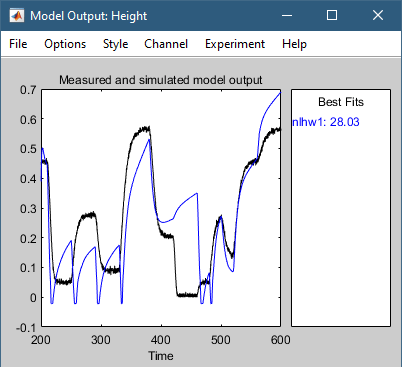
Модель nlhw1 неправильно проверяет. Соответствие zv.OutputData беден.
Нелинейность ввода/вывода и линейную передаточную функцию модели можно построить на графике Хаммерштейна-Винера.
В приложении «Идентификация системы» выберите Hamm-Wiener для просмотра графика модели Hammerstein-Wiener.
На графике отображается нелинейность входных данных, как показано на следующем рисунке.
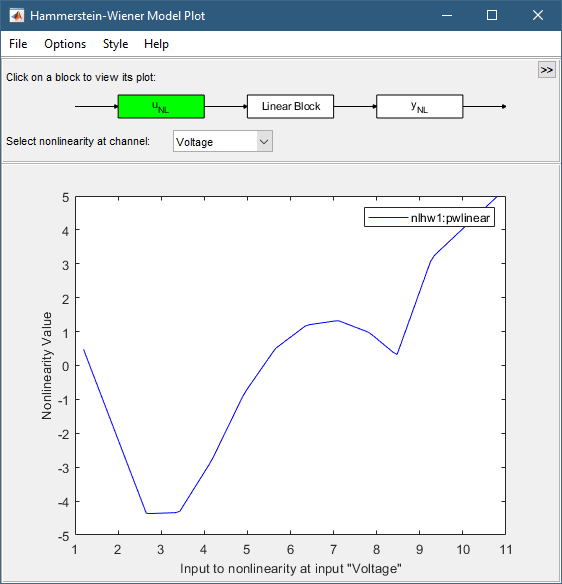
Щелкните прямоугольник yNL в верхней части окна графика модели Hammerstein-Wiener.
График обновляется для отображения нелинейности вывода.
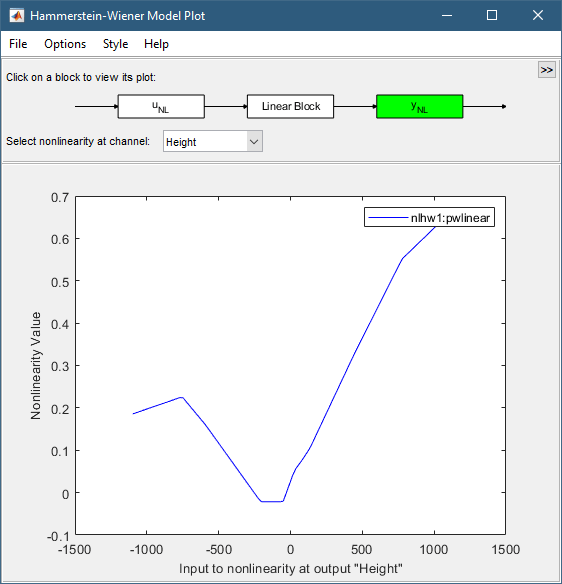
Щелкните прямоугольник «Линейный блок» в верхней части окна «Печать модели Хаммерштейна-Винера».
График обновляется для отображения ответа на шаг линейной передаточной функции.
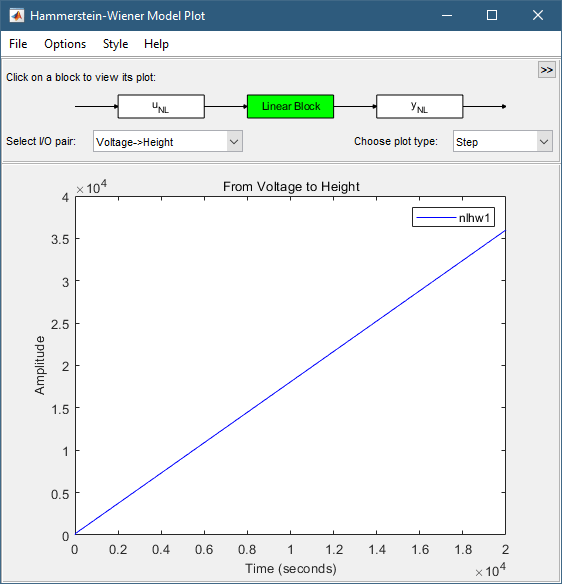
В списке «Выбор типа печати» выберите Bode. Это действие отображает график Боде функции линейного переноса.
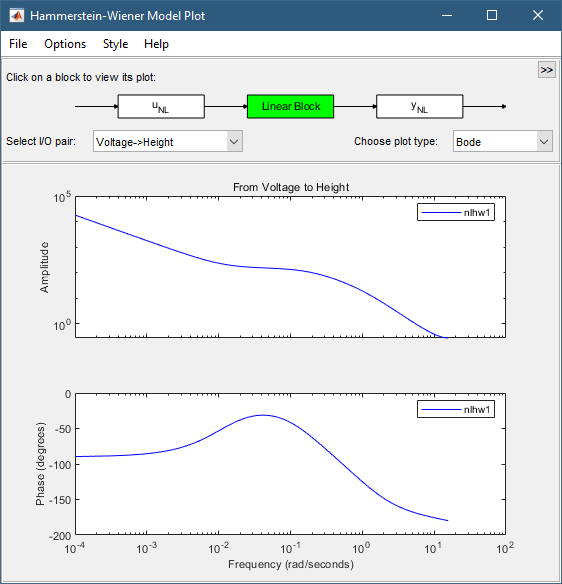
В этой части учебного пособия оценивается модель Хаммерштейна-Винера с определенным порядком модели и параметрами нелинейности. Обычно заказы моделей и задержки выбираются методом проб и ошибок до тех пор, пока модель не получит удовлетворительное соответствие данным.
Необходимо уже оценить модель Хаммерштейна-Винера с настройками по умолчанию, как описано в разделе Оценка моделей Хаммерштейна-Винера с настройками по умолчанию.
В диалоговом окне «Оценка Hammerstein-Wiener» выберите вкладку «Структура модели», а затем вкладку «Линейный блок».
Для Voltage входной канал, дважды щелкните на соответствующей ячейке задержки ввода (nk) и введите значение 3.
Щелкните Оценка (Estimate).
Это действие добавляет модель nlhw2 в приложение Идентификация системы (System Identification) и обновляет график Вывод модели (Model Output), как показано на следующем рисунке.
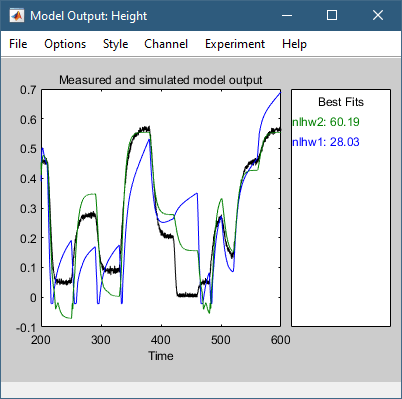
На панели «Наилучшие посадки» окна «Вывод модели» показано качество nlhw2 fit, что является улучшением по сравнению с моделью nlhw1.
В этой части примера структура модели Хаммерштейна-Винера по умолчанию изменяется путем изменения оценщика нелинейности.
Совет
Если известно, что система включает нелинейности насыщения или мертвых зон, можно указать эти специализированные оценки нелинейности в модели. Piecewise Linear, Wavelet Network, и Sigmoid Network являются оценщиками нелинейности для общей аппроксимации нелинейности.
В диалоговом окне Оценка моделей Хаммерштейна-Винера (Estimate Hammerstein-Wiener Models) выберите вкладку Структура модели (Model Structure), а затем вкладку Нелинейность ввода (Input Nonlinearity).
Щелкните ячейку Нелинейность (Nonlinearity) для Voltage переменная и выберите Sigmoid Network из списка.
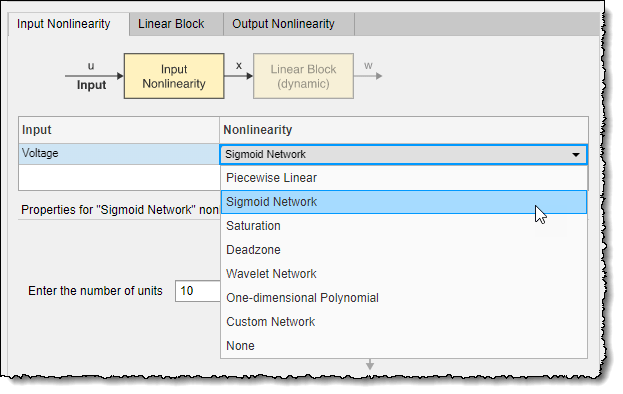
В поле «Введите количество единиц» задайте значение 20.
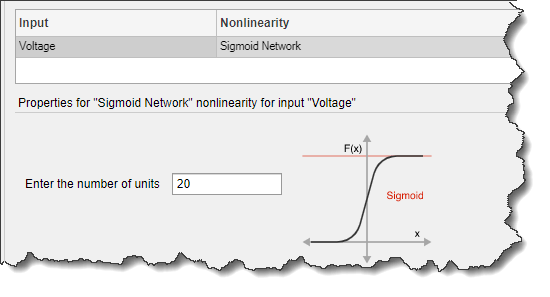
Щелкните Оценка (Estimate).
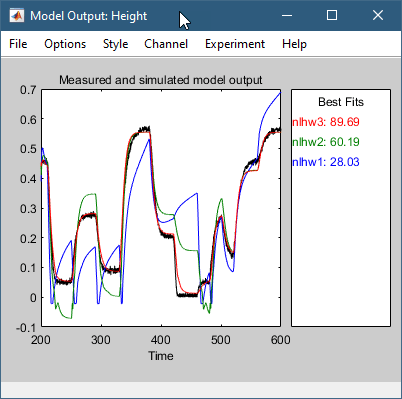
Это действие добавляет модель nlhw3 в приложении System Identification (Идентификация системы). Также обновляется окно Model Output (Вывод модели), как показано на следующем рисунке.
В диалоговом окне Оценка моделей Хаммерштейна-Винера (Estimate Hammerstein-Wiener Models) выберите вкладку Ввод нелинейности (Input Nonlinearity).
Для Voltage ввод, установите нелинейность в значение Wavelet Network. Значение по умолчанию для параметра Количество единиц измерения (Number of Units) - Выбрать автоматически (Select Automatically).
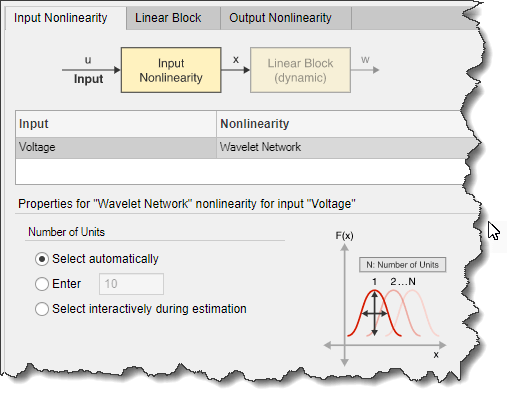
Выберите вкладку Вывод нелинейности (Output Nonlinearity).
Установите Height вывод нелинейности в One-dimensional Polynomial. Задать степень полинома как 2.
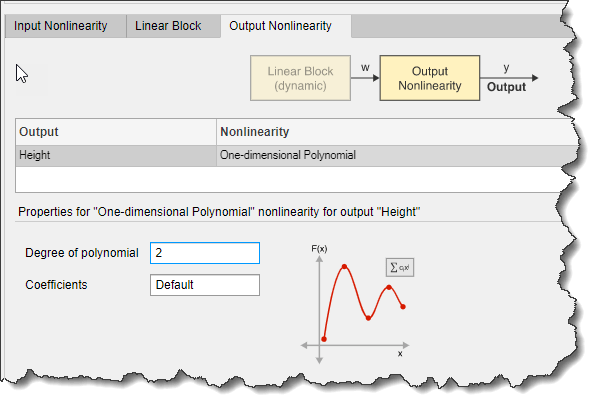
Щелкните Оценка (Estimate).
Это действие добавляет модель nlhw4 в приложении System Identification (Идентификация системы). Также обновляется окно Model Output (Вывод модели), как показано на следующем рисунке.
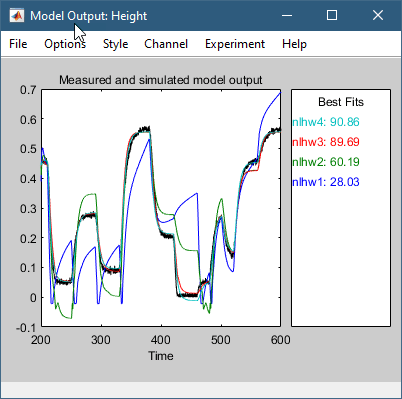
Лучшая модель - это простейшая модель, которая точно описывает динамику.
В этом примере модели nlhw3 и nlhw4 хорошие кандидаты.