Exponenta Banner
exponenta event banner

idnlarx

Нелинейная модель ARX

развернуть все на странице

Описание

Один idnlarx модель представляет нелинейную модель ARX, которая является расширением линейной структуры ARX и содержит линейные и нелинейные функции.

Нелинейная модель ARX состоит из регрессоров модели и выходной функции. Функция вывода включает в себя линейные и нелинейные функции, которые действуют на регрессоры модели для получения выходного сигнала модели и фиксированного смещения для этого выходного сигнала. Эта блок-схема представляет структуру нелинейной модели ARX в сценарии моделирования.

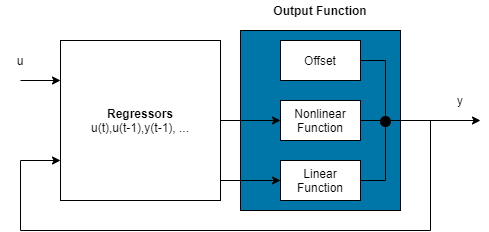
Regressor block is on the left. Output function is on the right. Output function block contains, from top to bottom, Offset, Nonlinear Function, and Linear Function. The inputs to the Regressor block are system input u and the output of the output function y.

Программное обеспечение вычисляет выход нелинейной модели ARX y в два этапа:

  1. Он вычисляет значения регрессора из текущих и прошлых входных значений и прошлых выходных данных.

    В простейшем случае регрессоры представляют собой запаздывающие входы и выходы, такие как u (t-1) и y (t-3). Такие регрессоры называются линейными регрессорами. Линейные регрессоры задаются с помощью linearRegressor объект. Можно также задать линейные регрессоры, используя линейные порядки моделей ARX в качестве входного аргумента. Дополнительные сведения см. в разделе Нелинейные заказы модели ARX и задержка. Однако этот второй подход ограничивает набор регрессоров линейными регрессорами с последовательными задержками. Для создания полиномиальных регрессоров используйте polynomialRegressor объект. Можно также указать пользовательские регрессоры, которые являются нелинейными функциями отложенных входов и выходов. Например, u (t-1) y (t-3) является пользовательским регрессором, который умножает экземпляры ввода и вывода вместе. Укажите пользовательские регрессоры с помощью customRegressor объект.

    Можно назначить любой из регрессоров в качестве входных данных линейному функциональному блоку выходной функции, нелинейному функциональному блоку или и тому и другому.

  2. Он отображает регрессоры на выходные данные модели с помощью функционального блока вывода. Выходной функциональный блок может включать в себя линейные и нелинейные блоки параллельно. Например, рассмотрим следующее уравнение:

    F (x) = LT (x − r) + g (Q (x − r)) + d

    Здесь x - вектор регрессоров, а r - среднее значение x. F (x) = LT (x − r) + y0 - выход линейного функционального блока. g (Q (x − r)) + y0 представляет выход нелинейного функционального блока. Q - это проекционная матрица, которая делает вычисления хорошо обусловленными. d - скалярное смещение, которое добавляется к объединенным выходам линейного и нелинейного блоков. Точная форма F (x) зависит от выбора функции вывода. Можно выбрать из доступных объектов отображения, таких как сети с древовидными разделами, вейвлет-сети и многослойные нейронные сети. Можно также исключить линейный или нелинейный функциональный блок из функции вывода.

    При оценке нелинейной модели ARX программное обеспечение вычисляет значения параметров модели, такие как L, r, d, Q, и другие параметры, определяющие g.

Результирующими нелинейными моделями ARX являются idnlarx объекты, хранящие все данные модели, включая регрессоры модели и параметры выходной функции. Дополнительные сведения об этих объектах см. в разделе Нелинейные структуры модели.

Для получения дополнительной информации о idnlarx см. раздел Что такое нелинейные модели ARX?.

Для idnlarx свойства объекта см. в разделе Свойства.

Создание

Вы можете получить idnlarx объект одним из двух способов.

  • Используйте nlarx для обеих конструкций idnlarx объект и оценка параметров модели.

    sys = nlarx(data,reg)

  • Используйте idnlarx конструктор для создания нелинейной модели ARX и последующей оценки параметров модели с помощью nlarx или pem.

    sys = idnlarx(output_name,input_name,reg)

Синтаксис

sys = idnlarx (output_name,input_name,orders)
sys = idnlarx (output_name,input_name,Regressors)
sys = idnlarx (___, OutputFcn)
sys = idnlarx (линмодель)
sys = idnlarx (linmodel, OutputFcn)
sys = idnlarx (___, имя, значение)

Описание

Указать модель непосредственно

пример

sys = idnlarx(output_name,input_name,orders) задает набор линейных регрессоров с использованием порядков моделей ARX. Этот синтаксис используется при расширении линейной модели ARX или при планировании использования только тех регрессоров, которые являются линейными с последовательными лагами.

пример

sys = idnlarx(output_name,input_name,Regressors) создает нелинейную модель ARX с выходными и входными именами output_name и input_name, соответственно, и набор регрессоров в регрессорах, который содержит любую комбинацию линейных, полиномиальных и пользовательских регрессоров. Программные конструкции sys с использованием вейвлет-сети по умолчанию ('wavenet') объект отображения для функции вывода.

пример

sys = idnlarx(___,OutputFcn) задает выходную функцию OutputFcn, которая сопоставляет регрессоры с выходными данными модели. Этот синтаксис можно использовать с любой из предыдущих комбинаций входных аргументов.

Инициализация значений модели с использованием линейной модели

пример

sys = idnlarx(linmodel) использует линейную модель linmodel для извлечения определенных свойств, таких как имена, единицы измерения и время выборки, а также для инициализации значений линейных коэффициентов модели. Этот синтаксис используется при создании нелинейной модели ARX в качестве расширения или улучшения существующей линейной модели.

пример

sys = idnlarx(linmodel,OutputFcn) задает выходную функцию OutputFcn, которая сопоставляет регрессоры с выходными данными модели.

Задание свойств модели

sys = idnlarx(___,Name,Value) задает дополнительные свойства idnlarx с использованием одного или нескольких аргументов «имя-значение».

Входные аргументы

развернуть все

Заказы модели ARX, указанные как матрица [na nb nk]. na обозначает количество задержанных выходов, nb обозначает количество отложенных входов, и nk обозначает минимальную задержку на входе. Минимальная задержка на выходе фиксирована на 1. Дополнительные сведения о построении orders матрица, см. arx.

При указании orders, программное обеспечение преобразует информацию о порядке в форму линейного регрессора в idnlarx Regressors собственность. Пример см. в разделе Создание нелинейной модели ARX с использованием заказов модели ARX.

Дискретно-временная идентифицированная линейная модель ввода/вывода, заданная как любая линейная модель, созданная с использованием оценщиков, то есть idpoly объект, idss объект, idtf объект или idproc объект с Ts > 0. Создайте эту модель с помощью функции конструктора для объекта или оцените модель с помощью связанной команды оценки. Например, чтобы создать модель ARX, используйте arxи укажите результирующий idpoly объект как linmodel.

Свойства

развернуть все

Спецификация регрессора, заданная как вектор столбца, содержащий один или несколько объектов спецификации регрессора, которые являются linearRegressor объекты, polynomialRegressor объекты, и customRegressor customRegressor объекты. Каждый объект задает формулу для создания регрессоров из запаздывающих переменных. Например:

  • L = linearRegressor({'y1','u1'},{1,[2 5]}) генерирует регрессоры y1 (t-1), u1 (t-2) и u2 (t-5).

  • P = polynomialRegressor('y2',4:7,2) генерирует регрессоры y2 (t-4) 2, y2 (t-5) 2, y2 (t-6) 2 и y2 (t-7) 2.

  • C = customRegressor({'y1','u1','u2'},{1 2 2},@(x,y,z)sin(x.*y+z)) генерирует одиночный sin-регрессор (y1 (t-1) u1 (t-2) + u2 (t-2)

    .

Пример реализации этих регрессоров см. в разделе Создание и объединение типов регрессоров.

Чтобы добавить регрессоры в существующую модель, создайте вектор объектов спецификации и используйте точечную нотацию для задания Regressors к этому вектору. Например, следующий код сначала создает idnlarx модель sys а затем добавляет объекты-регрессоры L, P, и C в регрессоры sys.

sys = idnlarx({'y1','y2'},{'u1','u2'});
R = [L;P;C];
sys.Regressors = R;

Пример создания и использования набора линейных регрессоров см. в разделе Создание нелинейной модели ARX с использованием линейных регрессоров.

Функция вывода, отображающая регрессоры idnlarx модель на выходе модели, заданная как массив столбцов, содержащий ноль или более следующих строк или объектов сопоставления:

'wavenet' или wavenet объектВейвлет-сеть
'linear' или '' или [] или linear объектЛинейная функция
'sigmoidnet' или sigmoidnet объектСигмоидная сеть
'treepartition' или treepartition объектМодель регрессии секционирования двоичного дерева
neuralnet объектНейронная сеть - Feedforward network of Deep Learning Toolbox™.
customnet объектПользовательская сеть - Аналогично sigmoidnet, но с определяемой пользователем заменой сигмоидной функции.

wavenet, sigmoidnet, treepartion, и customnet объекты содержат как линейные, так и нелинейные компоненты. Можно удалить (не использовать) линейные компоненты wavenet, sigmoidnet, и customnet путем установки LinearFcn.Use значение для false.

neuralnet имеет только нелинейный компонент, который является network (Deep Learning Toolbox) Объект Deep Learning Toolbox. Линейная функция, как следует из названия, имеет только линейный компонент.

Например, указание вектора символов 'sigmoidnet'создает объект сопоставления с параметрами по умолчанию. Можно также задать свойства объекта сопоставления двумя другими способами:

  • Создайте объект сопоставления с помощью аргументов для изменения свойств по умолчанию.

    MO = sigmoidnet(15)

  • Сначала создайте объект сопоставления по умолчанию, а затем используйте точечное представление для изменения свойств.

    MO = sigmoidnet;
MO.NumberOfUnits = 15

Для ny выходных каналов можно задать объекты отображения отдельно для каждого канала путем установки OutputFcn в массив ny объектов сопоставления. Например, следующий код определяет OutputFcn использование точечной нотации для системы с двумя входными каналами и двумя выходными каналами. 

sys = idnlarx({'y1','y2'},{'u1','u2'});
sys.OutputFcn = [wavenet; sigmoidnet]
Чтобы задать одинаковое сопоставление для всех выходов, укажите OutputFcn в виде символьного вектора или одиночного объекта сопоставления.

OutputFcn представляет функцию статического отображения, которая преобразует регрессоры нелинейной модели ARX в выходные данные модели. OutputFcn статичен, поскольку не зависит от времени. Например, если y (t) = y0 + a1y (t − 1) + a2y (t − 2) +... + b1u (t − 1) + b2u (t − 2) +..., тоOutputFcn - линейная функция, представленная linear объект.

Пример задания функции вывода см. в разделе Задание функции вывода для нелинейной модели ARX.

Назначения регрессоров линейным и нелинейным компонентам нелинейной модели ARX, заданные как таблица nr-by-nc с логическими записями, указывающими, какие регрессоры использовать для какого компонента. Здесь nr - количество регрессоров. nc - общее число линейных и нелинейных компонентов в OutputFcn. Строки таблицы соответствуют отдельным регрессорам. Имена строк устанавливаются в имена регрессоров. Если значение таблицы для строки i и индекса компонента j равно true, то i-й регрессор является входом в линейную или нелинейную составляющую j.

Для систем с несколькими выходами, OutputFcn содержит один объект сопоставления для каждого вывода. Каждый объект отображения может использовать как линейные, так и нелинейные компоненты или только один из этих двух компонентов.

Пример просмотра и изменения RegressorUsage см. раздел Изменение назначений регрессора компонентам выходных функций.

Это свойство доступно только для чтения.

Сводный отчет, содержащий информацию о вариантах оценки и результатах для нелинейной модели ARX, полученной с помощью nlarx команда. Использовать Report для поиска оценочной информации для идентифицированной модели, в том числе:

  • Метод оценки

  • Варианты оценки

  • Условия завершения поиска

  • Соответствие оценочных данных

Содержание Report не имеют значения, если модель была построена с использованием idnlarx.

sys = idnlarx('y1','u1',reg);
sys.Report.OptionsUsed
ans =

     []

Если вы используете nlarx для оценки модели, поля Report содержат информацию об оценочных данных, опциях и результатах.

load iddata1;
sys = nlarx(z1,reg);
m.Report.OptionsUsed
Option set for the nlarx command:

  IterativeWavenet: 'auto'
             Focus: 'prediction'
           Display: 'off'
    Regularization: [1x1 struct]
      SearchMethod: 'auto'
     SearchOptions: [1x1 idoptions.search.identsolver]
      OutputWeight: 'noise'
          Advanced: [1x1 struct]

Дополнительные сведения об этом свойстве и его использовании см. в разделе Выходные аргументы в разделе nlarx справочная страница и отчет об оценке.

Независимая переменная для входов, выходов и - при наличии - внутренних состояний, заданная как символьный вектор.

Дисперсия шума (ковариационная матрица) инноваций модели. Алгоритм оценки обычно устанавливает это свойство. Однако можно также назначить значения ковариации, указав nyоколо-ny матрица.

Время выборки, указанное как положительный скаляр, представляющий период выборки. Это значение выражается в единицах, указанных TimeUnit свойство модели.

Единицы измерения для переменной времени, времени выборки Tsи любые временные задержки в модели, указанные как одно из следующих значений:

  • 'nanoseconds'

  • 'microseconds'

  • 'milliseconds'

  • 'seconds'

  • 'minutes'

  • 'hours'

  • 'days'

  • 'weeks'

  • 'months'

  • 'years'

Изменение этого свойства не влияет на другие свойства и, следовательно, изменяет общее поведение системы. Использовать chgTimeUnit(Панель инструментов системы управления) для преобразования единиц времени без изменения поведения системы.

Имена входных каналов, указанные как одно из следующих:

  • Символьный вектор - для моделей с одним входом, например, 'controls'.

  • Массив ячеек символьных векторов - для моделей с несколькими входами.

Входные имена в нелинейных моделях ARX должны быть допустимыми именами переменных MATLAB ® после удаления пробелов.

Можно также использовать автоматическое векторное расширение для назначения входных имен для моделей с несколькими входами. Например, если sys является моделью с двумя входами, введите:

sys.InputName = 'controls';

Имена вводимых данных автоматически расширяются до {'controls(1)';'controls(2)'}.

При оценке модели с использованием iddata объект, data, программное обеспечение устанавливается автоматически InputName кому data.InputName.

Можно использовать сокращенную нотацию u см. InputName собственность. Например, sys.u эквивалентно sys.InputName.

Имена входных каналов имеют несколько применений, в том числе:

  • Идентификация каналов на дисплее модели и графиках

  • Извлечение подсистем систем MIMO

  • Указание точек соединения при соединении моделей

Блоки входных каналов, указанные как одно из следующих:

  • Символьный вектор - для моделей с одним входом, например, 'seconds'.

  • Массив ячеек символьных векторов - для моделей с несколькими входами.

Использовать InputUnit отслеживание блоков входных сигналов. InputUnit не влияет на поведение системы.

Группы входных каналов. InputGroup позволяет назначать входные каналы систем MIMO в группы и ссылаться на каждую группу по имени. Укажите входные группы как структуру. В этой структуре имена полей являются именами групп, а значения полей - входными каналами, принадлежащими каждой группе. Например:

sys.InputGroup.controls = [1 2];
sys.InputGroup.noise = [3 5];

создает входные группы с именем controls и noise которые включают в себя входные каналы 1, 2 и 3, 5 соответственно. Затем можно извлечь подсистему из controls входы на все выходы с использованием:

sys(:,'controls')

Имена выходных каналов, указанные как одно из следующих:

  • Символьный вектор - для моделей с одним выходом. Например, 'measurements'.

  • Массив ячеек символьных векторов - для моделей с несколькими выходами.

Выходные имена в нелинейных моделях ARX должны быть допустимыми именами переменных MATLAB после удаления пробелов.

Можно также использовать автоматическое векторное расширение для назначения выходных имен для моделей с несколькими выходами. Например, если sys является моделью с двумя выходами, введите:

sys.OutputName = 'measurements';

Имена вывода автоматически расширяются до {'measurements(1)';'measurements(2)'}.

При оценке модели с использованием iddata объект, data, программное обеспечение устанавливается автоматически OutputName кому data.OutputName.

Можно использовать сокращенную нотацию y см. OutputName собственность. Например, sys.y эквивалентно sys.OutputName.

Имена выходных каналов имеют несколько применений, в том числе:

  • Идентификация каналов на дисплее модели и графиках

  • Извлечение подсистем систем MIMO

  • Указание точек соединения при соединении моделей

Единицы выходного канала, указанные как одно из следующих:

  • Символьный вектор - для моделей с одним выходом. Например, 'seconds'.

  • Массив ячеек символьных векторов - для моделей с несколькими выходами.

Использовать OutputUnit отслеживание блоков выходного сигнала. OutputUnit не влияет на поведение системы.

Группы выходных каналов. OutputGroup позволяет назначать выходные каналы систем MIMO в группы и ссылаться на каждую группу по имени. Укажите группы вывода в качестве структуры. В этой структуре имена полей являются именами групп, а значения полей - выходными каналами, принадлежащими каждой группе. Например:

sys.OutputGroup.temperature = [1];
sys.InputGroup.measurement = [3 5];

создает выходные группы с именем temperature и measurement которые включают в себя выходные каналы 1 и 3, 5 соответственно. Затем можно извлечь подсистему из всех входов в measurement вывод с использованием:

sys('measurement',:)

Имя системы, указанное как символьный вектор. Например, 'system 1'.

Любой текст, который требуется связать с системой, указанный как строка или массив ячеек символьных векторов. Свойство хранит данные любого типа. Например, если sys1 и sys2 являются динамическими моделями систем, можно задать их Notes свойства следующим образом.

sys1.Notes = "sys1 has a string.";
sys2.Notes = 'sys2 has a character vector.';
sys1.Notes
sys2.Notes
ans = 

    "sys1 has a string."


ans =

    'sys2 has a character vector.'

Любые данные, которые требуется связать с системой, указанные как любой тип данных MATLAB.

Функции объекта

Сведения о функциях объекта для idnlarx, см. Нелинейные модели ARX.

Примеры

свернуть все

Открыть сценарий в реальном времени

Создание idnlarx путем задания вектора порядка модели ARX.

Создание вектора порядка формы [na nb nk], где na и nb - порядки многочленов модели A и B ARX и nk - количество задержек ввода/вывода.

na = 2;
nb = 3;
nk = 5;
orders = [na nb nk];

Построение нелинейной модели ARX sys.

output_name = 'y1';
input_name = 'u1';

sys = idnlarx(output_name,input_name,[2 3 5]);

Просмотрите функцию вывода.

disp(sys.OutputFcn)
Wavelet Network

 Nonlinear Function: Wavelet network with number of units chosen automatically.
 Linear Function: uninitialized
 Output Offset: uninitialized

           Input: [1×1 idpack.Channel]
          Output: [1×1 idpack.Channel]
       LinearFcn: [1×1 nlident.internal.UseProjectedLinearFcn]
    NonlinearFcn: [1×1 nlident.internal.WavenetFcn]
          Offset: [1×1 nlident.internal.ChooseableOffset]

По умолчанию модель использует вейвлет-сеть, представленную wavenet для функции вывода. wavenet объект включает линейный и нелинейный компоненты.

Просмотр Regressors собственность.

disp(sys.Regressors)
Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1 2]  [5 6 7]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

  Regressors described by this set

idnlarx конструктор преобразует заказы модели в Regressors форма.

  • Lags массив для y1, [1 2], эквивалентно na значение 2. Обе формы задают два последовательных выходных регрессора, y1(t-1) и y1(t-2).

  • Lags массив для u1, [5 6 7], включает три задержки, указанные nb значение 3 и сдвигает их на nk значение 5. Поэтому входными регрессорами являются u1(t-5), u1(t-6), и u1(t-7).

Просмотрите регрессоры.

getreg(sys)
ans = 5×1 cell
    {'y1(t-1)'}
    {'y1(t-2)'}
    {'u1(t-5)'}
    {'u1(t-6)'}
    {'u1(t-7)'}

Вы можете использовать orders для задания простых линейных регрессоров. Однако для создания более сложных регрессоров используйте команды регрессора linearRegressor, polynomialRegressor, и customRegressor для создания комбинированного регрессора для Regressors синтаксис.

Открыть сценарий в реальном времени

Построение idnlarx путем задания линейных регрессоров.

Создайте линейный регрессор, содержащий два выходных лага и два входных лага.

output_name = 'y1';
input_name = 'u1';
var_names = {output_name,input_name};

output_lag = [1 2];
input_lag = [1 2];
lags = {output_lag,input_lag};

reg = linearRegressor(var_names,lags)
reg = 
Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1 2]  [1 2]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

  Regressors described by this set

Модель содержит регрессоры y(t-1), y(t-2), u(t-1), и u(t-2).

Создайте idnlarx моделирование и просмотр регрессоров.

sys = idnlarx(output_name,input_name,reg);
getreg(sys)
ans = 4×1 cell
    {'y1(t-1)'}
    {'y1(t-2)'}
    {'u1(t-1)'}
    {'u1(t-2)'}

Просмотрите функцию вывода.

disp(sys.OutputFcn)
Wavelet Network

 Nonlinear Function: Wavelet network with number of units chosen automatically.
 Linear Function: uninitialized
 Output Offset: uninitialized

           Input: [1×1 idpack.Channel]
          Output: [1×1 idpack.Channel]
       LinearFcn: [1×1 nlident.internal.UseProjectedLinearFcn]
    NonlinearFcn: [1×1 nlident.internal.WavenetFcn]
          Offset: [1×1 nlident.internal.ChooseableOffset]

Просмотрите таблицу использования регрессора.

disp(sys.RegressorUsage)
               y1:LinearFcn    y1:NonlinearFcn
               ____________    _______________

    y1(t-1)       true              true      
    y1(t-2)       true              true      
    u1(t-1)       true              true      
    u1(t-2)       true              true

Все регрессоры являются входами как для линейных, так и для нелинейных компонентов wavenet объект.

Открыть сценарий в реальном времени

Создайте нелинейную модель ARX с линейным набором регрессоров.

Создайте линейный регрессор, содержащий три выходных лага и два входных лага.

output_name = 'y1';
input_name = 'u1';
var_names = {output_name,input_name};

output_lag = [1 2 3];
input_lag = [1 2];
lags = {output_lag,input_lag};

reg = linearRegressor(var_names,lags)
reg = 
Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1 2 3]  [1 2]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

  Regressors described by this set

Создайте нелинейную модель ARX.

sys = idnlarx(output_name,input_name,reg);

Просмотр Regressors собственность.

disp(sys.Regressors)
Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1 2 3]  [1 2]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

  Regressors described by this set

sys использование wavenet в качестве функции вывода по умолчанию. Реконфигурировать функцию вывода в sigmoidnet.

sys.OutputFcn = 'sigmoidnet';
disp(sys.OutputFcn)
Sigmoid Network

 Nonlinear Function: Sigmoid network with 10 units.
 Linear Function: uninitialized
 Output Offset: uninitialized

           Input: [1×1 idpack.Channel]
          Output: [1×1 idpack.Channel]
       LinearFcn: [1×1 nlident.internal.UseProjectedLinearFcn]
    NonlinearFcn: [1×1 nlident.internal.RidgenetFcn]
          Offset: [1×1 nlident.internal.ChooseableOffset]
Открыть сценарий в реальном времени

При построении нелинейной модели ARX укажите функцию вывода сигмоидной сети.

Назначьте имена переменных и укажите набор регрессоров.

output_name = 'y1';
input_name = 'u1';
r = linearRegressor({output_name,input_name},{1 1});

Создание нелинейной модели ARX, определяющей sigmoidnet функция вывода. Задайте число членов в сигмоидальном расширении равным 15.

sys = idnlarx(output_name,input_name,r,sigmoidnet(15));

Просмотрите спецификацию функции вывода.

disp(sys.OutputFcn)
Sigmoid Network

 Nonlinear Function: Sigmoid network with 15 units.
 Linear Function: uninitialized
 Output Offset: uninitialized

           Input: [1×1 idpack.Channel]
          Output: [1×1 idpack.Channel]
       LinearFcn: [1×1 nlident.internal.UseProjectedLinearFcn]
    NonlinearFcn: [1×1 nlident.internal.RidgenetFcn]
          Offset: [1×1 nlident.internal.ChooseableOffset]
Открыть сценарий в реальном времени

Построение idnlarx модель, использующая только линейное отображение в функции вывода. Значение аргумента [] эквивалентно значению аргумента 'linear'.

sys = idnlarx([2 2 1],[])
sys = 
Nonlinear ARX model with 1 output and 1 input
  Inputs: u1
  Outputs: y1

Regressors:
  Linear regressors in variables y1, u1
  List of all regressors

Model output is linear in regressors.
Sample time: 1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.
Открыть сценарий в реальном времени

Создайте набор регрессоров, включающий линейные, полиномиальные и пользовательские регрессоры.

Определить L в качестве набора линейных регрессоров y1 (t-1), u1 (t-2) и u1 (t-5).

L = linearRegressor({'y1','u1'},{1, [2 5]});

Определить P в качестве набора полиномиальных регрессоров y2 (t-4) 2, y2 (t-5) 2, y2 (t-6) 2 и y2 (t-7) 2.

P = polynomialRegressor('y2',4:7,2);

Определить C в качестве пользовательского регрессора sin (y1 (t-1) u1 (t-2) + u2 (t-2)), используя@ для создания анонимного дескриптора функции.

C = customRegressor({'y1','u1','u2'},{1 2 2},@(x,y,z)sin(x.*y+z));

Объединение регрессоров в один набор регрессоров R.

R = [L;P;C]
R=3×1 object
[3 1] array of linearRegressor, polynomialRegressor, customRegressor objects.
------------------------------------
1. Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1]  [2 5]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

------------------------------------
2. Order 2 regressors in variables y2
               Order: 2
           Variables: {'y2'}
                Lags: {[4 5 6 7]}
         UseAbsolute: 0
    AllowVariableMix: 0
         AllowLagMix: 0
        TimeVariable: 't'

------------------------------------
3. Custom regressor: sin(y1(t-1).*u1(t-2)+u2(t-2))
    VariablesToRegressorFcn: @(x,y,z)sin(x.*y+z)
                  Variables: {'y1'  'u1'  'u2'}
                       Lags: {[1]  [2]  [2]}
                 Vectorized: 1
               TimeVariable: 't'

  Regressors described by this set

Создайте нелинейную модель ARX.

sys = idnlarx({'y1','y2'},{'u1','u2'},R)
sys = 
Nonlinear ARX model with 2 outputs and 2 inputs
  Inputs: u1, u2
  Outputs: y1, y2

Regressors:
  1. Linear regressors in variables y1, u1
  2. Order 2 regressors in variables y2
  3. Custom regressor: sin(y1(t-1).*u1(t-2)+u2(t-2))
  List of all regressors

Output functions:
  Output 1: Wavelet Network
  Output 2: Wavelet Network

Sample time: 1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.
Открыть сценарий в реальном времени

Для построения нелинейной модели ARX используйте линейную модель ARX вместо набора регрессоров.

Построение линейной модели ARX с использованием idpoly.

A = [1 -1.2 0.5];
B = [0.8 1];
LinearModel = idpoly(A, B, 'Ts', 0.1);

Укажите входные и выходные имена для модели с помощью точечной нотации.

LinearModel.OutputName = 'y1';
LinearModel.InputName = 'u1';

Создайте нелинейную модель ARX с использованием линейной модели ARX.

m1 = idnlarx(LinearModel)
m1 = 
Nonlinear ARX model with 1 output and 1 input
  Inputs: u1
  Outputs: y1

Regressors:
  Linear regressors in variables y1, u1
  List of all regressors

Output function: Wavelet Network

Sample time: 0.1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.

Можно создать линейную модель ARX из любой идентифицированной дискретно-временной линейной модели.

Оценка модели пространства состояния второго порядка на основе оценочных данных z1.

load iddata1 z1
ssModel = ssest(z1,2,'Ts',0.1);

Построение нелинейной модели ARX из ssModel. Программное обеспечение использует входные и выходные имена, которые ssModel экстракты из z1.

m2 = idnlarx(ssModel)
m2 = 
Nonlinear ARX model with 1 output and 1 input
  Inputs: u1
  Outputs: y1

Regressors:
  Linear regressors in variables y1, u1
  List of all regressors

Output function: Wavelet Network

Sample time: 0.1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.
Открыть сценарий в реальном времени

Изменение назначений регрессора путем изменения RegressorUsage таблица.

Создайте нелинейную модель ARX с двумя входами и двумя выходами.

Создайте имена переменных и регрессоры.

varnames = {'y1','y2','u1','u2'};
lags = {[1 2 3],[1 2],[1 2],[1 3]};
reg = linearRegressor(varnames,lags);

Создание спецификации функции вывода fcn который использует wavenet для отображения регрессоров на выход y1 и sigmoidnet для отображения регрессоров на выход y2. Оба объекта отображения содержат линейные и нелинейные компоненты.

fcn = [wavenet;sigmoidnet];

Создайте нелинейную модель ARX.

output_name = {'y1' 'y2'};
input_name = {'u1' 'u2'};
sys = idnlarx(output_name,input_name,reg,fcn)
sys = 
Nonlinear ARX model with 2 outputs and 2 inputs
  Inputs: u1, u2
  Outputs: y1, y2

Regressors:
  Linear regressors in variables y1, y2, u1, u2
  List of all regressors

Output functions:
  Output 1: Wavelet Network
  Output 2: Sigmoid Network with 10 units

Sample time: 1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.

Отображение RegressorUsage таблица.

disp(sys.RegressorUsage)
               y1:LinearFcn    y1:NonlinearFcn    y2:LinearFcn    y2:NonlinearFcn
               ____________    _______________    ____________    _______________

    y1(t-1)       true              true             true              true      
    y1(t-2)       true              true             true              true      
    y1(t-3)       true              true             true              true      
    y2(t-1)       true              true             true              true      
    y2(t-2)       true              true             true              true      
    u1(t-1)       true              true             true              true      
    u1(t-2)       true              true             true              true      
    u2(t-1)       true              true             true              true      
    u2(t-3)       true              true             true              true

Строки таблицы представляют регрессоры. Первые два столбца таблицы представляют линейные и нелинейные компоненты отображения для вывода y1 (wavenet). Последние два столбца представляют два компонента сопоставления для вывода y2 (sigmoidnet).

В этой таблице все входные и выходные регрессоры являются входами для всех компонентов.

Удалить y2(t-2) регрессор из y2 нелинейный компонент.

sys.RegressorUsage{4,4}=false;
disp(sys.RegressorUsage)
               y1:LinearFcn    y1:NonlinearFcn    y2:LinearFcn    y2:NonlinearFcn
               ____________    _______________    ____________    _______________

    y1(t-1)       true              true             true              true      
    y1(t-2)       true              true             true              true      
    y1(t-3)       true              true             true              true      
    y2(t-1)       true              true             true              false     
    y2(t-2)       true              true             true              true      
    u1(t-1)       true              true             true              true      
    u1(t-2)       true              true             true              true      
    u2(t-1)       true              true             true              true      
    u2(t-3)       true              true             true              true

Отображается таблица false для этой пары регрессор-компонент.

Удалить все выходные регрессоры из y1 нелинейный компонент.

Store regressor names in Names.

Names = sys.RegressorUsage.Properties.RowNames;

Определение индексов строк, содержащих y1 или y2 и установить соответствующие значения y1:NonlinearFcn кому False.

idx = contains(Names,'y1')|contains(Names,'y2');
sys.RegressorUsage{idx,2} = false;
disp(sys.RegressorUsage)
               y1:LinearFcn    y1:NonlinearFcn    y2:LinearFcn    y2:NonlinearFcn
               ____________    _______________    ____________    _______________

    y1(t-1)       true              false            true              true      
    y1(t-2)       true              false            true              true      
    y1(t-3)       true              false            true              true      
    y2(t-1)       true              false            true              false     
    y2(t-2)       true              false            true              true      
    u1(t-1)       true              true             true              true      
    u1(t-2)       true              true             true              true      
    u2(t-1)       true              true             true              true      
    u2(t-3)       true              true             true              true

Значения таблицы отражают новые назначения.

RegressorUsage таблица обеспечивает полную гибкость для индивидуального управления назначениями регрессоров.

Подробнее

развернуть все

Вопросы совместимости

развернуть все

Не рекомендуется начинать с R2021a

См. также

| | | | | | | | | |

Темы

Представлен в R2007a

Документация по инструментам идентификации системы

Поддержка