Нелинейные модели ARX расширяют линейные модели ARX до нелинейного варианта. Структура этих моделей позволяет моделировать сложное нелинейное поведение с использованием гибких нелинейных функций, таких как вейвлет и сигмоидные сети. Сведения о том, когда вписываться в нелинейные модели, см. в разделе Сведения об идентифицированных нелинейных моделях.
Линейная модель SISO ARX имеет следующую структуру:
1) +... + bnbu (t − nb + 1) + e (t)
Где, u, y и e - вход, выход и шум. Эта структура подразумевает, что токовый выход y (t) прогнозируется как взвешенная сумма прошлых выходных значений и текущих и прошлых входных значений. na - число прошлых выходных терминов, а nb - число прошлых входных терминов, используемых для прогнозирования текущего выходного сигнала. Входная задержка nk устанавливается равной нулю для упрощения обозначения. Переписывание уравнения как произведения дает:
), u (t − 1),..., u (t − nb − 1)] T
где 1),..., u (t − nb − 1) - запаздывающие входные и выходные переменные, называемые регрессорами. Вектор коэффициентов [-a1,..., bnb] представляет взвешивание, применяемое к этим регрессорам. Таким образом, линейная модель ARX предсказывает токовый выход yp как взвешенную сумму его регрессоров.
Структура нелинейной модели ARX обеспечивает следующую дополнительную гибкость:
Вместо взвешенной суммы регрессоров, которые представляют линейное отображение, нелинейная модель ARX имеет более гибкую функцию нелинейного отображения, F.
u (t − 1), u (t − 2),..)
Входы в F являются модельными регрессорами. При указании нелинейной структуры модели ARX можно выбрать одну из нескольких доступных нелинейных функций. Например, F может представлять взвешенную сумму вейвлетов, которые работают на расстоянии регрессоров от их средств. Дополнительные сведения см. в разделе Доступные функции сопоставления для нелинейных моделей ARX.
Нелинейные ARX-регрессоры могут быть как запаздывающими переменными ввода-вывода, так и более сложными нелинейными выражениями запаздывающих входных и выходных переменных. Примерами таких нелинейных регрессоров являются y (t-1) 2, u (t-1) * y (t-2), abs (u (t-1)) и max (u (t-1) * y (t-3), -10).
Нелинейная модель ARX состоит из регрессоров модели и выходной функции. Функция вывода включает в себя линейные и нелинейные функции, которые действуют на регрессоры модели для получения выходного сигнала модели и фиксированного смещения для этого выходного сигнала. Эта блок-схема представляет структуру нелинейной модели ARX в сценарии моделирования.
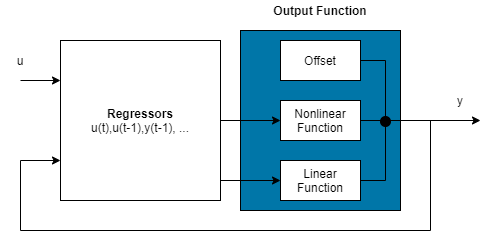
Программное обеспечение вычисляет выход нелинейной модели ARX y в два этапа:
Он вычисляет значения регрессора из текущих и прошлых входных значений и прошлых выходных данных.
В простейшем случае регрессоры представляют собой запаздывающие входы и выходы, такие как u (t-1) и y (t-3). Такие регрессоры называются линейными регрессорами. Линейные регрессоры задаются с помощью linearRegressor объект. Можно также задать линейные регрессоры, используя линейные порядки моделей ARX в качестве входного аргумента. Дополнительные сведения см. в разделе Нелинейные заказы модели ARX и задержка. Однако этот второй подход ограничивает набор регрессоров линейными регрессорами с последовательными задержками. Для создания полиномиальных регрессоров используйте polynomialRegressor объект. Можно также указать пользовательские регрессоры, которые являются нелинейными функциями отложенных входов и выходов. Например, u (t-1) y (t-3) является пользовательским регрессором, который умножает экземпляры ввода и вывода вместе. Укажите пользовательские регрессоры с помощью customRegressor объект.
Можно назначить любой из регрессоров в качестве входных данных линейному функциональному блоку выходной функции, нелинейному функциональному блоку или и тому и другому.
Он отображает регрессоры на выходные данные модели с помощью функционального блока вывода. Выходной функциональный блок может включать в себя линейные и нелинейные блоки параллельно. Например, рассмотрим следующее уравнение:
Q (x − r)) + d
Здесь x - вектор регрессоров, а r - среднее значение x. r) + y0 - выход линейного функционального (x − r)) + y0 представляет выход нелинейного функционального блока. Q - это проекционная матрица, которая делает вычисления хорошо обусловленными. d - скалярное смещение, которое добавляется к объединенным выходам линейного и нелинейного блоков. Точная форма F (x) зависит от выбора функции вывода. Можно выбрать из доступных объектов отображения, таких как сети с древовидными разделами, вейвлет-сети и многослойные нейронные сети. Можно также исключить линейный или нелинейный функциональный блок из функции вывода.
При оценке нелинейной модели ARX программное обеспечение вычисляет значения параметров модели, такие как L, r, d, Q, и другие параметры, определяющие g.
Результирующими нелинейными моделями ARX являются idnlarx объекты, хранящие все данные модели, включая регрессоры модели и параметры выходной функции. Дополнительные сведения об этих объектах см. в разделе Нелинейные структуры модели.
Как правило, нелинейные модели ARX используются в качестве структур черного ящика. Нелинейная функция нелинейной модели ARX представляет собой гибкий оценщик нелинейности с параметрами, которые не обязательно имеют физическую значимость. Нелинейный ARX можно оценить в приложении System Identification или в командной строке с помощью nlarx команда. Для оценки нелинейных моделей ARX можно использовать однородные данные ввода-вывода временной области или данные временных рядов (без входных данных). Данные могут иметь один или несколько каналов ввода и вывода. Нельзя использовать данные частотной области для оценки.
Для определения линейных регрессоров модели можно использовать порядки и задержки нелинейной модели ARX. Заказы и задержка определяются следующим образом:
na - количество прошлых выходных терминов, используемых для прогнозирования текущего выходного сигнала.
nb - количество прошлых входных терминов, используемых для прогнозирования токового выхода.
nk - Задержка от входа к выходу в терминах количества выборок.
Значение na, nb и nk аналогично значению для параметров линейной модели ARX. Порядки задаются как скаляры для данных SISO и как матрицы ny-by-nu для данных MIMO, где ny и nu - количество выходов и входов. Если нет уверенности в том, какие значения следует использовать для заказов и задержек, их можно оценить, как описано в разделе Предварительный шаг - Оценка модельных заказов и задержек ввода. Такая оценка основана на линейных моделях ARX и дает только начальное руководство. Наилучшие заказы для линейной модели ARX могут не быть лучшими заказами для нелинейной модели ARX.
Программное обеспечение System Identification Toolbox™ вычисляет линейные регрессоры, используя порядки моделей и задержки. Например, предположим, что вы указали na = 2, nb = 3, и nk = 5 для модели SISO с входными u и выходными y. Панель инструментов вычисляет линейные регрессоры y (t-2), y (t-1), u (t-5), u (t-6) и u (t-7).
Вместо того чтобы использовать порядок модели ARX для определения задержек регрессоров, можно также указать регрессоры непосредственно для фиксации более сложного поведения. При непосредственном указании линейных регрессоров можно включить несектутивные элементы задержки. Можно также задать полиномиальные регрессоры и пользовательские регрессоры. Дополнительные сведения см. в разделах Оценка нелинейных моделей ARX в приложениях и Оценка нелинейных моделей ARX в командной строке.