Exponenta Banner
exponenta event banner

Оценка нелинейных моделей ARX в командной строке

Нелинейные модели ARX можно оценить после выполнения следующих задач.

Оценка модели с использованием nlarx

Использовать nlarx для построения и оценки нелинейной модели ARX. После каждой оценки проверьте модель, сравнивая ее с другими моделями и моделируя или прогнозируя ответ модели.

Базовая оценка

Начните с простейшей оценки с помощью m = nlarx(data,[na nb nk]). Например:

load iddata1;
% na = nb = 2 and nk = 1 
m = nlarx(z1,[2 2 1])
m = 
Nonlinear ARX model with 1 output and 1 input
  Inputs: u1
  Outputs: y1

Regressors:
  Linear regressors in variables y1, u1
  List of all regressors

Output function: Wavelet Network with 1 unit

Sample time: 0.1 seconds

Status:                                          
Estimated using NLARX on time domain data "z1".  
Fit to estimation data: 68.83% (prediction focus)
FPE: 1.975, MSE: 1.885

Просмотрите регрессоры.

getreg(m)
ans = 4×1 cell
    {'y1(t-1)'}
    {'y1(t-2)'}
    {'u1(t-1)'}
    {'u1(t-2)'}

Второй входной аргумент [na nb nk] определяет заказы модели и задержки. По умолчанию функция вывода - вейвлет-сеть wavenet, который принимает регрессоры в качестве входных данных для своих линейных и нелинейных функций. m является idnlarx объект.

Для систем MIMO nb, nf, и nk - матрицы ny-by-nu. См. раздел nlarx для получения дополнительной информации об оценке MIMO.

Создание nlarxOptions установить и сконфигурировать Focus для минимизации ошибки моделирования.

opt = nlarxOptions('Focus','simulation');
M = nlarx(z1,[2 2 1],'sigmoid',opt);

Настройка регрессоров модели

Линейные регрессоры

Линейные регрессоры представляют линейные функции, которые основаны на задержанных входных и выходных переменных и которые обеспечивают входные данные для выходной функции модели. При использовании заказов для задания модели количество входных регрессоров равно na и количество выходных регрессоров равно nb. Синтаксис заказов ограничивает последовательные задержки. Можно также создать линейные регрессоры с помощью linearRegressor. При использовании linearRegressor, можно указать произвольные задержки.

Полиномиальные регрессоры

Изучение возможности использования полиномиальных регрессоров polynomialRegressor в дополнение к линейным регрессорам в структуре нелинейной модели ARX. Полиномиальные регрессоры - полиномиальные функции запаздывающих входов и выходов. (см. Нелинейные заказы и задержки модели ARX).

Например, создайте полиномиальные регрессоры до порядка 2.

P = polynomialRegressor({'y1','u1'},{[1],[2]},2);

Добавьте полиномиальные регрессоры к линейным регрессорам в m.Regressors.

m.Regressors = [m.Regressors;P];
getreg(m)
ans = 8×1 cell
    {'y1(t-1)'  }
    {'y1(t-2)'  }
    {'u1(t-1)'  }
    {'u1(t-2)'  }
    {'y1(t-3)'  }
    {'y1(t-5)'  }
    {'y1(t-1)^2'}
    {'u1(t-2)^2'}

m теперь включает полиномиальные регрессоры.

Просмотр размера m.Regressors массив.

size(m.Regressors)
ans = 1×2

     3     1

Теперь массив содержит три объекта-регрессора.

Пользовательские регрессоры

Использовать customRegressor для построения регрессоров как произвольных функций входных и выходных переменных модели.

. Например, создайте два пользовательских регрессора, которые реализуют 'sin(y1(t-1)' и 'y1(t-2).*u1(t-3)'.

C1 = customRegressor({'y1'},{1},@(x)sin(x));
C2 = customRegressor({'y1','u1'},{2,3},@(x,y)x.*y);
m.Regressors = [m.Regressors;C1;C2];
getreg(m) % displays all regressors
ans = 10×1 cell
    {'y1(t-1)'         }
    {'y1(t-2)'         }
    {'u1(t-1)'         }
    {'u1(t-2)'         }
    {'y1(t-3)'         }
    {'y1(t-5)'         }
    {'y1(t-1)^2'       }
    {'u1(t-2)^2'       }
    {'sin(y1(t-1))'    }
    {'y1(t-2).*u1(t-3)'}

Просмотр свойств пользовательских регрессоров. Например, получить дескриптор функции первого пользовательского регрессора в массиве. Этот регрессор является четвертым регрессором в Regressors массив.

C1_fcn = m.Regressors(4).VariablesToRegressorFcn
C1_fcn = function_handle with value:
    @(x)sin(x)

Просмотрите описание регрессора.

display(m.Regressors(4))
Custom regressor: sin(y1(t-1))
    VariablesToRegressorFcn: @(x)sin(x)
                  Variables: {'y1'}
                       Lags: {[1]}
                 Vectorized: 1
               TimeVariable: 't'

  Regressors described by this set

Комбинированные регрессоры

После создания линейных, полиномиальных и пользовательских объектов-регрессоров их можно комбинировать любым способом, который соответствует потребностям оценки.

Задание входов регрессора для линейных и нелинейных компонентов

Регрессоры модели могут вводиться в качестве входных данных для одного или обоих линейных и нелинейных компонентов функций отображения, составляющих выходную функцию. Чтобы уменьшить сложность модели и поддерживать оценку в хорошем состоянии, рассмотрите возможность назначения уменьшенного набора регрессоров нелинейному компоненту. Линейному компоненту можно также назначить подмножество регрессоров. Таблица использования регрессора, управляющая назначениями, обеспечивает полную гибкость. Каждому компоненту можно назначить любую комбинацию регрессоров. Например, укажите нелинейную модель ARX, которая должна быть линейной на прошлых выходах и нелинейной на прошлых входах.

m = nlarx(z1,[2 2 1]); 
disp(m.RegressorUsage)
               y1:LinearFcn    y1:NonlinearFcn
               ____________    _______________

    y1(t-1)       true              true      
    y1(t-2)       true              true      
    u1(t-1)       true              true      
    u1(t-2)       true              true      

m.RegressorUsage{3:4,1} = false;
m.RegressorUsage{1:2,2} = false;
disp(m.RegressorUsage)
               y1:LinearFcn    y1:NonlinearFcn
               ____________    _______________

    y1(t-1)       true              false     
    y1(t-2)       true              false     
    u1(t-1)       false             true      
    u1(t-2)       false             true

Настройка функции вывода

В следующей таблице представлены доступные объекты сопоставления для функции вывода модели.

Описание сопоставленияЗначение (конфигурация объекта сопоставления по умолчанию)Объект сопоставления
Вейвлет-сеть
(по умолчанию)		'wavenet' или 'wave'wavenet
Одноуровневая сигмоидальная сеть'sigmoidnet' или 'sigm'sigmoidnet
Раздел дерева'treepartition' или 'tree'treepartition
F является линейным в x'linear' или [ ] или ''linear

Дополнительные доступные объекты отображения включают многослойные нейронные сети и создаваемые пользовательские сети.

Укажите многослойную нейронную сеть, используя:

m = nlarx(data,[na nb nk],NNet)

где NNet - нейронный сетевой объект, созданный с помощью программного обеспечения Deep Learning Toolbox™. См. раздел neuralnet справочная страница.

Укажите пользовательскую сеть, определив функцию gaussunit.m, как описано в customnet справочная страница. Определение пользовательского сетевого объекта CNetw и оценить модель:

CNetw = customnet(@gaussunit);
m = nlarx(data,[na nb nk],CNetw)

Исключить линейную функцию в выходной функции

Если функция вывода модели включает wavenet, sigmoidnet, или customnet отображение объектов, линейную функцию можно исключить с помощью LinearFcn.Use свойства объекта сопоставления. Объект отображения становится F (x) = g (Q (x − r)) + y0, где g (.) - нелинейная функция, а y0 - смещение.

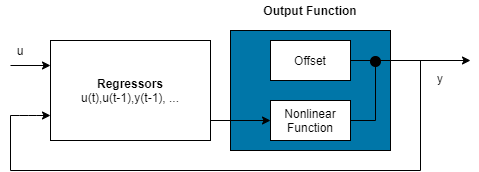
Примечание

Нельзя исключить линейную функцию из древовидной секции и объектов отображения нейронной сети.

Исключить нелинейную функцию из функции вывода

Настройте нелинейную структуру ARX для включения только линейной функции в объект отображения, установив для объекта сопоставления значение linear. В этом случае F (x) = LT (x − r) + y0 - взвешенная сумма регрессоров модели плюс смещение. Такие модели обеспечивают мостик между чисто линейными ARX моделями и полностью гибкими нелинейными моделями.

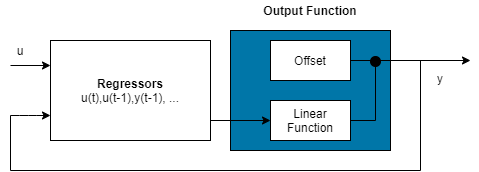
Популярная нелинейная конфигурация ARX во многих приложениях использует полиномиальные регрессоры для моделирования нелинейности системы. В таких случаях система считается линейной комбинацией произведений (отложенных) входных и выходных переменных. Используйте polynomialRegressor команда легко генерировать комбинации продуктов-регрессоров и сил.

Например, предположим, что выход y (t) системы должен быть линейной комбинацией (y (t − 1)) 2, (u (t − 1)) 2 и y (t − 1) u (t − 1)). Для моделирования такой системы используются:

P = polynomialRegressor({'y1','u1'},{1,1},2)
P = 
Order 2 regressors in variables y1, u1
               Order: 2
           Variables: {'y1'  'u1'}
                Lags: {[1]  [1]}
         UseAbsolute: [0 0]
    AllowVariableMix: 0
         AllowLagMix: 0
        TimeVariable: 't'

  Regressors described by this set

P.AllowVariableMix = true;
M = nlarx(z1,P,'linear');
getreg(M)
ans = 3×1 cell
    {'y1(t-1)^2'      }
    {'u1(t-1)^2'      }
    {'y1(t-1)*u1(t-1)'}

Для более сложных комбинаций полиномиальных задержек и смешанно-переменных регрессоров можно также использовать customRegressor.

Итеративное уточнение модели

Если структура модели включает объекты сопоставления, поддерживающие итеративный поиск (см. раздел Определение опций оценки для нелинейных моделей ARX), можно использовать nlarx для уточнения параметров модели:

m1 = nlarx(z1,[2 2 1],'sigmoidnet');
m2 = nlarx(z1,m1); % can repeatedly run this command

Также можно использовать pem для уточнения исходной модели:

m2 = pem(z1,m1);

Проверка критерия завершения поиска m.Report.Termination.WhyStop . Если WhyStop указывает, что оценка достигла максимального числа итераций, попробуйте повторить оценку и, возможно, укажите большее значение для nlarxOptions.SearchOptions.MaxIterations вариант оценки:

opt = nlarxOptions;
opt.SearchOptions.MaxIterations = 30;
m2 = nlarx(z1,m1,opt); % runs 30 more iterations
                               % starting from m1

Когда m.Report.Termination.WhyStop значение равно Near (local) minimum, (norm( g) < tol или No improvement along the search direction with line search проверьте модель, чтобы убедиться, что она соответствует данным. В противном случае решение может застрять в локальном минимуме поверхности «стоимость-функция». Попробуйте изменить параметры поиска.Tolerance значение или SearchMethod в наборе опций nlarxOptions и повторите оценку.

Можно также попытаться нарушить параметры последней модели с помощью init (называется рандомизацией) и уточнение модели с использованием nlarx: 

M1 = nlarx(z1, [2 2 1], 'sigmoidnet'); % original model
M1p = init(M1);	% randomly perturbs parameters about nominal values
M2 = nlarx(z1, M1p);  % estimates parameters of perturbed model

Можно просмотреть ход итеративного поиска в окне команд MATLAB с помощью nlarxOptions.Display вариант оценки:

opt = nlarxOptions('Display','on');
M2= nlarx(z1,M1p,opt);

Устранение неполадок при оценке

Если вы не получите удовлетворительную модель после многих испытаний с различными структурами модели и настройками алгоритма, возможно, что данные плохи. Например, в данных могут отсутствовать важные входные или выходные переменные и они недостаточно охватывают все рабочие точки системы.

Нелинейная идентификация системы черного ящика обычно требует больше данных, чем линейная идентификация модели, чтобы получить достаточно информации о системе.

Использование nlarx для оценки нелинейных моделей ARX

Открыть сценарий в реальном времени

В этом примере показано, как использовать nlarx для оценки нелинейной модели ARX для измеренных входных/выходных данных.

Подготовить данные для оценки.

load twotankdata
z = iddata(y, u, 0.2);
ze = z(1:1000); zv = z(1001:3000);

Оцените несколько моделей, используя различные порядки моделей, задержки и нелинейные настройки.

m1 = nlarx(ze,[2 2 1]);
m2 = nlarx(ze,[2 2 3]);
m3 = nlarx(ze,[2 2 3],wavenet(8));

Альтернативным способом выполнения оценки является сначала конфигурирование структуры модели, а затем оценка этой модели.

m4 = idnlarx([2 2 3],sigmoidnet(14));
m4.RegressorUsage.("y1:NonlinearFcn")(3:4) = false;
m4 = nlarx(ze,m4);

Сравните полученные модели, выведя выходные данные модели на график с измеренными выходными данными.

compare(zv, m1,m2,m3,m4)

См. также

Функции

Связанные темы

Документация по инструментам идентификации системы

Поддержка