Нелинейные модели ARX расширяют линейную модель ARX до нелинейного варианта. Сведения о структуре нелинейных моделей ARX см. в разделе Что такое нелинейные модели ARX?
Нелинейные модели ARX можно оценить в приложении System Identification или в командной строке с помощью nlarx команда. Для оценки нелинейной модели ARX сначала необходимо подготовить данные оценки. Затем необходимо настроить структуру модели и алгоритм оценки, а затем выполнить оценку. После оценки можно проверить оценочную модель, как описано в разделе Проверка нелинейных моделей ARX.
Для оценки нелинейных моделей ARX можно использовать однородные данные ввода-вывода временной области или данные временных рядов (без входных данных). Данные могут иметь нулевой или более входных каналов и один или более выходных каналов. Нельзя использовать данные частотной области для оценки.
Чтобы подготовить данные для оценки модели, импортируйте данные в рабочую область MATLAB ® и выполните одно из следующих действий.
В приложении Идентификация системы - импорт данных в приложение, как описано в разделе Представление данных.
В командной строке - представление данных в виде iddata объект.
После импорта данных можно анализировать качество данных и данные предварительной обработки путем интерполяции отсутствующих значений, фильтрации для выделения определенного частотного диапазона или повторной выборки с использованием другого времени выборки. Дополнительные сведения см. в разделе Способы подготовки данных для идентификации системы. Для большинства приложений перед нелинейным моделированием не требуется удалять смещения и линейные тренды из данных. Однако сдерживание данных может быть полезным в некоторых случаях, например, перед моделированием взаимосвязи между изменением входных и выходных данных относительно рабочей точки.
После подготовки оценочных данных можно настроить структуру модели, функцию потерь и алгоритм оценки, а затем оценить модель с помощью оценочных данных.
Нелинейная модель ARX состоит из набора регрессоров, которые могут быть любой комбинацией линейных, полиномиальных и пользовательских регрессоров, и выходной функции, которая обычно содержит нелинейный и линейный компонент, а также статическое смещение. Блок-схема представляет структуру нелинейной модели ARX в сценарии моделирования.
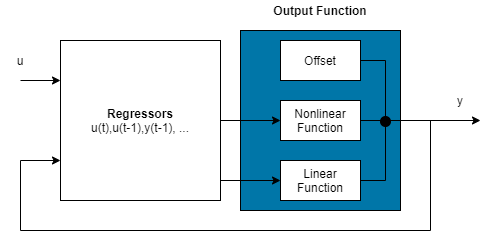
Конфигурирование структуры нелинейной модели ARX:
Сконфигурируйте регрессоры модели.
Выберите линейные, полиномиальные и пользовательские регрессоры на основе ваших знаний о физической системе, которую вы пытаетесь моделировать.
Задайте линейные регрессоры одним из следующих способов.
Укажите порядок моделей и задержку для создания набора линейных регрессоров. Дополнительные сведения см. в разделе Нелинейные заказы модели ARX и задержка.
Прямое определение линейных регрессоров путем конструирования и использования linearRegressor объекты.
Инициализируйте модель с помощью линейной модели ARX. Эту операцию можно выполнить только в командной строке. Инициализация настраивает нелинейную модель ARX для использования линейных регрессоров линейной модели. Дополнительные сведения см. в разделе Инициализация нелинейной оценки ARX с использованием линейной модели.
Укажите полиномиальные регрессоры и пользовательские регрессоры. Полиномиальные регрессоры - это полиномы, которые состоят из запаздывающих входных и выходных переменных. Пользовательские регрессоры - это произвольные функции прошлых входов и выходов, такие как произведения, мощности и другие MATLAB-выражения входных и выходных переменных. Укажите полиномиальные и пользовательские регрессоры в дополнение к линейным регрессорам или вместо них для большей гибкости моделирования данных. Дополнительные сведения см. в разделе polynomialRegressor и customRegressor.
Назначьте регрессоры в качестве входных данных для линейных и нелинейных компонентов выходного функционального блока. Любой регрессор может быть назначен любому или обоим из этих компонентов. Ограничение числа регрессоров, которые вводятся в нелинейный компонент, может помочь снизить сложность модели и поддерживать оценку в хорошем состоянии.
Выбор регрессоров для каждого компонента может потребовать нескольких испытаний. Можно изучить нелинейный график ARX, чтобы получить представление о том, какие регрессоры сильнее всего влияют на выходные данные модели. Понимание относительной важности регрессоров на выходе может помочь в выборе способа назначения регрессоров.
Сконфигурируйте функциональный блок вывода.
Укажите и сконфигурируйте функцию вывода F (x).
Q (x − r)) + d
Здесь x - вектор регрессоров, а r - среднее значение регрессоров x. r) + y0 - выход линейного функционального (x − r)) + y0 представляет выход нелинейного функционального блока. Q является проекционной матрицей, которая делает вычисления хорошо обусловленными. d - скалярное смещение, которое добавляется к объединенным выходам линейного и нелинейного блоков. Точная форма F (x) зависит от выбора функции вывода. Можно выбрать из доступных оценщиков нелинейности, таких как сети с древовидными разделами, вейвлет-сети и многослойные нейронные сети. Можно также исключить линейный или нелинейный функциональный блок из функции вывода.
Также можно выполнить одну из следующих задач:
Исключите нелинейную функцию из выходной функции так, чтобы F (x) = − r) + y0.
Исключите линейную функцию из выходной функции так, чтобы F (x) = )) + y0.
Примечание
Нельзя исключить линейную функцию из разделов дерева и нейронных сетей.
Сведения о настройке структуры модели в командной строке и в приложении см. в разделах Оценка нелинейных моделей ARX в командной строке и Оценка нелинейных моделей ARX в приложении.
Чтобы настроить оценку модели, укажите минимизируемую функцию потерь и выберите алгоритм оценки и другие опции оценки для выполнения минимизации.
Функция потерь или функция затрат является функцией ошибки между выходом модели и измеренным выходом. Дополнительные сведения о функциях потерь см. в разделах Функция потерь и Показатели качества модели.
В командной строке используйте команду nlarx набор опций, nlarxOptions для конфигурирования функции потери. Можно задать следующие параметры:
Focus - указывает, минимизируется ли ошибка моделирования или прогнозирования во время оценки параметров. По умолчанию программное обеспечение минимизирует ошибки одношагового прогнозирования, которые соответствуют Focus значение 'prediction'. Если требуется модель, оптимизированная для воспроизведения поведения моделирования, укажите Focus как 'simulation'. Минимизация ошибки моделирования требует дифференцированных нелинейных функций и требует больше времени, чем минимизация ошибки прогнозирования на один шаг вперед. Таким образом, вы не можете использовать treepartition и neuralnet нелинейности при минимизации ошибки моделирования, поскольку эти нелинейные оценки не дифференцируются.
OutputWeight - определяет взвешивание ошибки в оценках с несколькими выходами.
Regularization - изменяет функцию потерь, добавляя штраф к отклонению расчетных параметров. Дополнительные сведения см. в разделе Регуляризованные оценки параметров модели.
Для оценки нелинейной модели ARX программное обеспечение использует итеративные алгоритмы поиска, чтобы минимизировать ошибку между моделируемым или прогнозируемым выходом модели и измеряемым выходом. В командной строке используйте nlarxOptions для задания алгоритма поиска и других параметров оценки. Можно указать следующие параметры:
SearchMethod - Метод поиска для минимизации ошибок прогнозирования или моделирования, таких как поиск линий Гаусса-Ньютона и Левенберга-Марквардта, и подход Траста-Регион-Отражающий Ньютон.
SearchOptions - Набор опций для алгоритма поиска с полями, зависящими от значения SearchMethod, например:
MaxIterations - максимальное число итераций.
Tolerance - условие для завершения итеративного поиска, когда ожидаемое улучшение значений параметра меньше указанного значения.
Полный список доступных опций оценки см. в разделе nlarxOptions. Дополнительные сведения о том, как указать эти параметры оценки в приложении, см. в разделе Оценка нелинейных моделей ARX в приложении.
После предварительной обработки данных оценки и настройки структуры модели и опций оценки можно оценить модель в приложении System Identification или с помощью nlarx в командной строке. Результирующей моделью является idnlarx объект, хранящий все данные модели, включая регрессоры модели и параметры оценщика нелинейности. Дополнительные сведения об этих объектах модели см. в разделе Нелинейные структуры модели. Можно проверить расчетную модель, как описано в разделе Проверка нелинейных моделей ARX.
В командной строке можно использовать модель полинома структуры ARX (idpoly только с A и B в качестве активных многочленов) для нелинейной оценки ARX. Дополнительные сведения об использовании линейных моделей см. в разделе Когда подгонять нелинейные модели.
Как правило, линейная модель ARX создается с помощью arx команда. Линейную модель можно предоставить при построении или оценке нелинейной модели ARX. Например, используйте следующий синтаксис для оценки нелинейной модели ARX с использованием данных оценки и линейной модели ARX. LinARXModel.
m = nlarx(data,LinARXModel)
Здесь m является idnlarx объект, и data является временной областью iddata объект. Программное обеспечение использует линейную модель для инициализации нелинейной оценки ARX посредством:
Назначение порядков и задержек линейной модели ARX в качестве начальных значений порядков нелинейной модели ARX (na и nb свойства idnlarx объект) и задержки (nk свойство). Программное обеспечение использует эти порядки и задержки для вычисления линейных регрессоров в нелинейной структуре модели ARX.
Использование многочленов A и B линейной модели для вычисления линейной функции оценщиков нелинейности (LinearCoef параметр объекта оценки нелинейности), за исключением случая, когда оценщиком нелинейности является нейронная сеть.
Во время оценки алгоритм оценки использует эти значения для корректировки нелинейной модели на данные.
Примечание
При использовании тех же данных для оценки нелинейная модель ARX, инициализированная с использованием линейной модели ARX, обеспечивает лучшее соответствие измеренным выходным данным, чем сама линейная модель ARX.
По умолчанию оценщиком нелинейности является вейвлет-сеть (wavenet объект). Можно также указать различные входные и выходные нелинейные оценки. Например, можно указать сигмоидальный оценщик нелинейности сети.
m = nlarx(data,LinARXModel,'sigmoid')Пример см. в разделе Оценка нелинейных моделей ARX, инициализированных с помощью линейных моделей ARX.