Для тел с пользовательским поперечным сечением блоки Выдавленное тело (Extruded Solid) и Повернутое тело (Revolved Solid) позволяют создавать более правдивые представления тел, чем такие простые формы, как Кирпичное тело (Brick Solid), Цилиндрическое тело (Cylindrical Solid) и Сферическое тело (Spherical Solid). Они используются при моделировании тел с произвольным, но постоянным поперечным сечением вдоль или вокруг оси. Блок «Выдавленное твердое тело» может быть либо General выдавливание или Regular экструзия.
Общее выдавливание - это линейное протягивание пользовательского поперечного сечения вдоль оси, перпендикулярной плоскости поперечного сечения. Протягивание охватывает длину, заданную в диалоговом окне «Выдавленный твердотельный блок». Поперечное сечение может иметь произвольный контур и одно или несколько полых сечений, хотя правила задания поперечных сечений при наличии отверстий немного различаются.
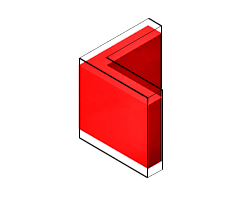
Общие примеры экструзии включают прямые балки, пластины, лонжероны, стойки и стержни. На чертеже показана угловая балка, общая экструзия, поперечное сечение которой состоит из двух тонких прямоугольников, расположенных в L-образной форме. Блок Выдавленное твердое тело (Extruded Solid) линейно вытягивает L-форму из плоскости поперечного сечения для получения конечной геометрии балки.
Общий вытянутый твердотельный блок как линейный сдвиг
Заметка о выдавленных твердотельных формах. Блок Выдавленное твердое тело (Extruded Solid) предоставляет вторую форму выдавливания, названную Regular экструзия. Эта форма является более простой версией General выдавливание и подходит только для твердых тел, поперечные сечения которых являются правильными многоугольниками - с сторонами одинаковой длины. Контур поперечного сечения фиксируется количеством сторон многоугольника и не может содержать отверстий.
Используйте блок «Тело вращения» (Revolved Solid) для создания углового сдвига поперечного сечения вокруг оси, лежащей на той же плоскости, что и поперечное сечение. Сдвиг может охватывать полный оборот или меньший угол между 0 и 360 степени. Как и в случае выдавленных форм, поперечное сечение может иметь произвольный контур с отверстиями или без них.
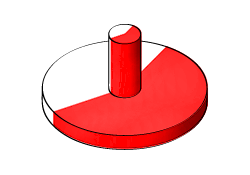
Примеры вращения включают конусы, купола, поршни, зубчатые валы и изгибы труб. На рисунке показан цилиндрический выступ, обращенное тело, поперечное сечение которого, подобно угловой балке, состоит из двух тонких прямоугольников, расположенных в L-образной форме. Блок Повернутое тело (Revolved Solid) протягивает L-форму вокруг оси, лежащей на плоскости поперечного сечения, чтобы получить конечную геометрию привязки.
Повернутое тело как угловой сдвиг
Сечения указываются численно, как матрицы MATLAB, заполненные координатными парами выбранных точек сечения. Каждая строка матрицы предоставляет пару координат для одной точки. Верхняя граница для числа строк матрицы координат отсутствует, но для полного определения замкнутой формы требуется минимум три.
% Coordinate Matrix Example: % Square Cross-Section with Center at [0, 0] and Side Length 2 [ -1 -1; % Lower left corner 1 -1; % Lower right corner 1 1; % Upper right corner -1 1; % Upper left corner ]
Пары координат обрабатываются как (x, y) значения в случае выдавленных форм и как (x, z) значения, заданные в этом порядке, в случае повернутых форм. Координаты разрешаются в опорном кадре блока Выдавленное тело (Extruded Solid) или Повернутое тело (Revolved Solid), причем пара (0, 0) совпадает с началом координат этого кадра. Обычной практикой является параметризация координат в терминах переменных MATLAB, связанных с ключевыми твердыми размерами - например, радиусом или длиной.
Пары координат последовательно соединяются в порядке, неявном для матрицы координат. Соединения выполняются посредством прямолинейных сегментов. Результатом является замкнутая полилиния, которая отделяет область, подлежащую заполнению материалом (твердая часть), от области, которая должна быть оставлена полой (любые отверстия, которые могут присутствовать, и пустые окрестности).
Граница между двумя областями такова, что при переходе вдоль полилинии от одной точки к другой сплошная область лежит слева, а полая область - справа. Первая и последняя пары координат часто одинаковы, но если их нет, между ними вставляется соединительная линия, чтобы гарантировать, что поперечное сечение действительно закрыто. Анимированный рисунок показывает рисунок бинарного поперечного сечения звена без отверстий.

Обратите внимание, что сечение является недопустимым, если в какой-либо точке полилиния пересекает сама себя. Однако вполне допустимо, чтобы два отрезка линии были произвольно близки друг к другу или даже совпадали друг с другом. Фактически это свойство можно использовать для задания поперечного сечения с одним или несколькими отверстиями.
Матрицы координат Повернутого тела (Revolved Solid) подвержены особому ограничению: координаты X не могут быть отрицательными. Это правило частично следует из оси вращения (z), используемой блоком тела вращения. При протягивании поперечного сечения любые области слева от этой оси (области с отрицательными координатами x) перекрываются с областями справа (положительной x), что приводит к неожиданной твердотельной геометрии. Чтобы предотвратить эту проблему, выдается ошибка, если обнаружено сечение тела вращения с отрицательными координатами x.
Рассмотрим поперечное сечение, показанное на рисунке. Это поперечное сечение принадлежит бинарному звену со скругленными концами и без отверстий. Параметризуйте поперечное сечение с учетом показанных размеров и укажите его в виде матрицы координат.
Поперечное сечение двоичной связи (без отверстий)
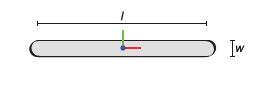
Начните с открытия нового скрипта MATLAB и сохраните его в удобном месте под именем modelParams. Добавьте две переменные для размеров, показанных на рисунке, длина (l) и ширина (w). Задайте длину как 20 и ширина до 2 (в том, что позже будет единиц cm).
l = 20;
w = 2; Определите концы скругления как полукруги. Сначала создайте два массива с угловыми пролетами левого и правого концов. Эти массивы позволяют параметризовать (x, y) с использованием простых тригонометрических выражений. Каждый массив имеет пять точек, но для более гладких фигур можно указать больше. Символ транспонирования (') гарантирует, что A и B являются массивами столбцов.
A = linspace(-pi/2, pi/2, 5)';
B = linspace(pi/2, 3*pi/2, 5)';Определите матрицы координат правого конца (csRight) и левый конец (csLeft). Первый столбец каждой матрицы соответствует координате X. Второй столбец соответствует координате y. Координаты X двух концов смещены в противоположных направлениях на l/2.
csRight = [l/2 + w/2*cos(A) w/2*sin(A)];
csLeft = [-l/2 + w/2*cos(B) w/2*sin(B)];Объединение матриц координат в одну матрицу с именем cs. Это матрица, которую необходимо задать в параметре «Поперечное сечение» (Cross-Section) блока «Тело вращения» (Revolved Solid). Следует отметить, что прямые сегменты поперечного сечения создаются автоматически при соединении конечных точек полуокружностей.
cs = [csRight; csLeft];Контур поперечного сечения можно визуализировать с помощью MATLAB
®plot команда. Введите следующий код в командной строке MATLAB.
figure; hold on; axis equal; plot(cs(:,1), cs(:,2), 'Color', [0.6 0.6 0.6], 'Marker', '.',... 'MarkerSize', 9, 'MarkerEdgeColor', [1 0 0]);
На графике показано поперечное сечение двоичной ссылки. Точки в матрице координат отображаются красными точками. Полученный контур поперечного сечения показан в виде светло-серой линии. Обратите внимание, что каждая концевая секция состоит из пяти точек - количество, указанное в массивах угловых пролетов.

Матрица координат всегда должна представлять один непрерывный путь. Это правило хорошо работает при указании сечения без отверстий, но требует дополнительной осторожности при наличии отверстий. Поскольку контур отверстия не является смежным с контуром поперечного сечения, теперь необходимо добавить тонкий вырез между ними. Вырез позволяет пересекать поперечное сечение и контуры отверстий в одном контуре.
Рассмотрим бинарную связь с отверстием на одном конце. Поперечное сечение этого корпуса содержит две замкнутые дорожки - одна для контура поперечного сечения, другая для отверстия. Пути физически разделены. Однако их можно соединить, разрезав каждую траекторию в вершине и соединив вершины реза с дополнительными сегментами линий. На анимированном рисунке показан чертеж поперечного сечения двоичной связи с одним отверстием.

Этот подход можно распространить на сечения с несколькими отверстиями. Обратите внимание, что каждое отверстие должно иметь вырез. Нет единого наилучшего способа подойти к вырубкам. Ключ состоит в том, чтобы спланировать их таким образом, чтобы можно было пересекать поперечное сечение - и все его отверстия - по одной непрерывной траектории, не допуская пересечения полилинии. На анимированном рисунке показан рисунок поперечного сечения двоичной связи с двумя отверстиями.

Изменение матрицы координат в modelParams для включения двух одинаковых отверстий, как показано на рисунке. Часто сохраняйте сценарий.
Поперечное сечение двоичного звена (два отверстия)
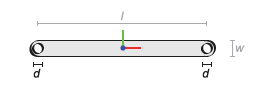
Начните с добавления новой переменной для диаметра отверстия (d). Задайте диаметр равным 1.2 (в том, что позже будет единиц cm).
d = 1.2;Создайте новый массив углового пролета для левого и правого отверстий. Отверстия вычерчиваются в том же порядке, и достаточно одного массива. Элементы массива упорядочены по часовой стрелке, что гарантирует, что при создании поперечного сечения сплошная область остается слева. Количество элементов матрицы удвоилось, чтобы отразить более широкий угловой пролет отверстий (360 ° против 180 °).
C = linspace(3*pi/2, -pi/2, 10)';Определите контуры левого отверстия (csLeftHole), правое отверстие (csRightHole) и соединительную линию между ними (csConnLine). Координаты x сдвинуты влево на половину длины (l/ 2) для левого отверстия и правого на одинаковое расстояние для правого отверстия.
csLeftHole = [-l/2 + d/2*cos(C) d/2*sin(C)];
csRightHole = [+l/2 + d/2*cos(C) d/2*sin(C)];
csConnLine = [-l/2 -w/2; +l/2 -w/2];Добавление новых матриц координат к существующим cs матрица. Порядок матриц определяет порядок, в котором рисуется полное сечение. Результатом является переменная, которую можно задать в параметре «Поперечное сечение» блока «Тело вращения».
cs = [csRight; csLeft; csLeftHole; ...
csConnLine; csRightHole];Как и ранее, можно визуализировать контур поперечного сечения с помощью MATLAB. plot команда. Убедитесь, что приведенный ниже код печати включен в сценарий. Затем запустите сценарий для создания графика.
figure; hold on; axis equal; plot(cs(:,1), cs(:,2), 'Color', [0.6 0.6 0.6], 'Marker', '.',... 'MarkerSize', 9, 'MarkerEdgeColor', [1 0 0]);
На графике показано поперечное сечение двоичной ссылки. Точки в матрице координат отображаются красными точками. Полученный контур поперечного сечения показан в виде светло-серой линии. Обратите внимание, что каждая из секций отверстия состоит из десяти точек - количество, указанное в массивах угловых пролетов.

Ось Z опорной рамки служит осью протягивания в блоках Выдавленное тело (Extruded Solid) и Повернутое тело (Revolved Solid). Указанное поперечное сечение протягивается вдоль этой оси в случае блока Выдавленное тело (Extruded Solid) и вокруг этой оси в случае блока Повернутое тело (Revolved Solid). Протягивание симметрично относительно плоскости поперечного сечения: оно проходит половину длины протягивания или угла в каждом направлении оси протягивания. Эта симметрия оставляет плоскость поперечного сечения - и, следовательно, начало отсчета - на полпути между концами протягивания.
Откройте новую модель Simulink ® и из библиотеки «Тела» добавьте блок «Выдавленное твердое тело». Можно щелкнуть холст модели, ввести имя блока и сделать выбор из показанных опций. Сохранение модели в удобном месте binaryLinkSolid.
В диалоговом окне «Выдавленный твердотельный блок» задайте параметры геометрии, как показано в таблице. Установите единицы измерения параметров в значение cm. Параметр Поперечное сечение (Cross-Section) определяется в терминах cs переменная в вашей modelParams сценарий.
| Параметр | Стоимость |
|---|---|
| Поперечное сечение | cs |
| Длина | 1 |
Загрузите ваш modelParams сценарий в рабочее пространство модели:
На вкладке Моделирование (Modeling) щелкните Обозреватель моделей (Model Explorer). Этот инструмент используется для загрузки modelParams сценарий, ранее созданный в рабочем пространстве модели.
На панели Иерархия модели (Model Hierarchy) разверните узел, соответствующий модели (binureLinkSolid), и выберите Модель (Model) Рабочее пространство (Workspace).
На панели Рабочее пространство модели (Model Workspace) задайте для параметра Источник данных (Data source) значение MATLAB File и найдите modelParams сценарий. Нажмите кнопку «Повторно инициализировать из источника», чтобы загрузить переменные, определенные в сценарии.
В диалоговом окне «Выдавленный твердотельный блок» нажмите кнопку «Обновить визуализацию». ![]() Панель визуализации обновляется с помощью конечной твердотельной геометрии.
Панель визуализации обновляется с помощью конечной твердотельной геометрии.
Нажмите кнопку «Вписать в вид», чтобы масштабировать двоичную ссылку до размера панели визуализации. Нажмите кнопку «Переключить видимость рамок», чтобы показать твердотельную опорную рамку. Начало отсчета совпадает с координатой поперечного сечения [0, 0] и лежит на полпути между концами выдавливания.
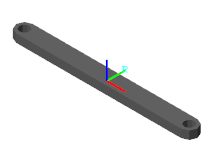
Обратите внимание на зазубренный вид концов скругления и отверстий. Этот эффект является результатом небольшого числа точек, используемых в участках скругления матрицы координат -csLeftEnd, csRightEnd, csLeftHole, и csRightHole. Увеличьте число элементов в массивах угловых пролетов, чтобы получить более гладкую геометрию.