Интерпретация нормы H-бесконечности

Нормы сигналов и систем

Существует несколько способов определения норм скалярного сигнала e (t) во временной области. Мы часто будем использовать 2-норма, (_{L2-норма}), для математического удобства, который определяется как

$‖_{} {e‖2:=_{(}^{} {∫−∞∞e}^{(} t)}^{\frac{}{}} 2dt$ ) 12.

Если этот интеграл является конечным, то сигнал e является квадратным интегрируемым, обозначаемым как e ∊ _L2. Для векторных сигналов

$e (t) \begin{matrix} =_{} [e1 \\ _{(} t) \\ {e2}_{} (t) \end{matrix}$ ⋮en (t)],

2-норма определяется как

$\begin{matrix} ‖_{} {e‖2:=_{(}^{} {∫−∞∞‖e}_{}^{} (t) ‖}^{\frac{}{}} \\ {22dt)_{}^{12}^{=} (∫−∞∞eT (}^{\frac{t}{)}} \end{matrix}$ e (t) dt) 12.

Динамические системы, с которыми мы имеем дело, являются исключительно линейными, с моделью «состояние-пространство»

$[\begin{matrix} \overset{}{} \end{matrix} \begin{matrix} x˙e]=[ABCD \end{matrix}] \begin{matrix} [ \end{matrix} xd$ ],

или, в форме передаточной функции,

e (s) = T (s) d (s), T (s): = C (^sI-A) -1B + D

Двумя математически удобными измерениями матрицы передачи T (s) в частотной области являются _H2 матрицы и нормы _H∞,

$\begin{array}{l} ‖_{} {\frac{}{}_{}^{} {T‖2:=[12π\int-\infty\infty‖T (джом}_{)}^{} ‖}^{\frac{}{}} \\ _{} \underset{}{\overset{}{}} F2dω]12‖T‖\infty:=maxσ¯ω\inR[T ( \end{array}$ джом)],

где норма Фробениуса (см. MATLAB ®norm команда) комплексной матрицы M

$‖_{} \sqrt{M‖F:=Trace^{(} М} *$ М).

Обе эти нормы передаточных функций имеют интерпретацию временной области ввода/вывода. Если, начиная с начального условия x (0) = 0, два сигнала d и e связаны

$[\begin{matrix} \overset{}{} \end{matrix} \begin{matrix} x˙e]=[ABCD \end{matrix}] \begin{matrix} [ \end{matrix} xd$ ],

тогда

Для d, единичной интенсивности, процесса белого шума, установившаяся дисперсия e равна ∥T∥2.
Коэффициент усиления L2 (или RMS) от d → e,
$\underset{}{} \frac{_{}}{_{maxd≠0‖e‖2‖d‖2}}$
равно ∥T∥∞. Этот вопрос более подробно рассматривается в следующем разделе.

Использование взвешенных норм для характеристики производительности

Любой критерий эффективности также должен учитывать

Относительная величина внешних воздействий
Частотная зависимость сигналов
Относительная важность величин регулируемых переменных

Таким образом, если цель производительности находится в форме матричной нормы, она фактически должна быть взвешенной нормой

_∥WLTWR∥

где матрицы _WL и _WR весовых функций зависят от частоты, для учета ограничений полосы пропускания и спектрального содержания экзогенных сигналов. Наиболее естественным (математическим) способом характеристики приемлемой производительности является норма MIMO _∥·∥∞ (H∞). По этой причине в данном разделе рассматриваются некоторые толкования H∞ нормы.

Невзвешенная система MIMO

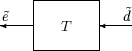
Предположим, что T - стабильная линейная система MIMO с матрицей T (s) передаточных функций. Для данного сигнала возбуждения $\overset{}{} d˜ ($ t) $\overset{}{определите}$ e˜ в качестве выходного сигнала, как показано ниже.

Обратите внимание, что традиционнее писать диаграмму в невзвешенной системе MIMO: Векторы слева направо со стрелками слева направо, как в взвешенной системе MIMO.

Невзвешенная система MIMO: векторы слева направо

Две схемы, показанные выше, представляют одну и ту же систему. Мы предпочитаем писать эти блок-схемы со стрелками, идущими справа налево, чтобы соответствовать матрице и составу оператора.

Предположим, что размеры T являются _ne × _nd. Пусть β > 0 определяется как

$_{} \underset{]}{\overset{}{} β:=‖T‖∞:=maxσ¯[T (jλ)}$ ω∈R.

Теперь рассмотрим ответ, начиная с начального условия, равного 0. В этом случае теорема Парсеваля дает, что

$\frac{{‖ \overset{}{}}_{}}{{\overset{}{}}_{}} \frac{{_{}^{} {\overset{}{}}^{} e˜‖2‖d˜‖2=[\int0\inftye˜T (t \overset{}{)} e˜ (t)}^{\frac{}{}}}{{_{}^{} {\overset{}{}}^{} dt]12[∫0∞d˜T \overset{(}{} t) d˜}^{\frac{(}{t}}})$ dt]12≤β.

Кроме того, существуют специфические нарушения d, которые приводят к отношению ${‖ \overset{}{}}_{} e˜‖2 {/ \overset{‖}{}}_{}$ d˜‖2 произвольно близкому к β. Из-за этого _∥T∥∞ называется L2 (или среднеквадратичным) усилением системы.

Как и следовало ожидать, возможна также синусоидальная, стационарная интерпретация ∥T∥∞: Для любого частотного $\overset{}{} ω¯∈R$ любой вектор амплитуд $_{_{a∈Rnd}}$ , и любой вектор фаз $^{_{ϕ∈Rnd}}$ , с помощью ∥a∥2 ≤ 1, определяют сигнал времени

$\overset{d˜}{} (t) \begin{matrix} =_{} [\overset{a1sin}{} (λ_{} bett \\ _{_{+}} δ 1) \overset{}{}_{_{}} ⋮andsin \end{matrix} ($ λ bett + δ nd)].

Применение этого входного сигнала к системе Т приводит к установившемуся ${\overset{}{}}_{e˜ss}$ отклика формы

${\overset{}{}}_{e˜ss} (t) \begin{matrix} =_{[} \overset{}{b1sin} (_{ω¯t} \\ {+ϕ1}_{)_{}} \overset{}{} ⋮bnesin (_{_{}} ω¯t \end{matrix}$ +ϕne)].

Вектор $^{_{b∈Rne}}$ будет удовлетворять ∥b∥2 ≤ β. Кроме того, β, как определено во Взвешенной Системе MIMO, является самым маленьким количеством, таким образом, что это верно для каждого ∥a∥2 ≤ 1, $\overset{ω¯}{}$ , и ϕ.

Заметим, что в этой интерпретации векторы синусоидальных откликов величины не взвешиваются и измеряются в евклидовой норме. Если реалистичные цели производительности с несколькими переменными должны быть представлены одной задачей _∥·∥∞ MIMO для функции передачи с замкнутым контуром, необходимы дополнительные масштабирования. Поскольку многие различные цели объединяются в одну матрицу, и связанные затраты являются нормой матрицы, важно использовать зависящие от частоты функции взвешивания, так что различные требования могут быть значимо объединены в одну функцию затрат. Наиболее легко интерпретируются диагональные веса.

Рассмотрим схему взвешенной системы MIMO наряду с невзвешенной системой MIMO: векторы слева направо.

Предположим, что _WL и _WR являются матрицами диагональных стабильных передаточных функций с диагональными элементами, обозначенными _Li и _Ri.

$_{WL} = \begin{matrix} _{[} \\ {L10..}_{.} \\ 00L2.. & _{_{}} \end{matrix} {0⋮⋮⋱⋮00...}_{} \begin{matrix} _{} & Lne & ] \\ , & _{} & WR \\ = & [ \\ {R10..}_{._{}} \end{matrix}$ 00R2.. 0⋮⋮⋱⋮00... Rnd].

Взвешенная система MIMO

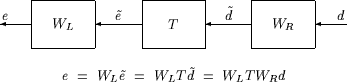
Границы на _{∥WLTWR∥∞} величины будут подразумевать границы синусоидального стационарного поведения сигналов $\overset{}{}$ d˜and $\overset{e˜}{} (\overset{}{} =Td˜$ ) на диаграмме невзвешенной системы MIMO: Векторы слева направо. В частности, для синусоидального сигнала $\overset{}{}$ d˜ отношение установившегося состояния между $\overset{}{} e˜ (\overset{}{}$ =Td˜) $\overset{}{,}$ d˜ и _{∥WLTWR∥∞} является следующим. Стационарное ${\overset{}{решение}}_{}$ e˜ss, обозначенное как

{\overset{}{}}_{e˜ss} (t) \begin{matrix} {\overset{[}{=}}_{} \overset{}{e˜1sin} (_{ω¯t} \\ {\overset{)}{+ϕ1}}_{_{}} \overset{}{} ⋮e˜nesin (_{_{}} ω¯t \end{matrix}

+ϕnd)]

(1)

удовлетворяет

$_{}^{_{}} {_{_{∑i=1ne'WLi}} (\overset{jλ)}{} {\overset{}{}}_{}}^{}$ e˜i|2≤1

для всех синусоидальных входных сигналов $\overset{d˜}{}$ вида

\tilde{d} (t) \begin{matrix} {\overset{[}{=}}_{} \overset{}{d˜1sin} (_{ω¯t} \\ {\overset{)}{+ϕ1}}_{_{}} \overset{}{} ⋮d˜nesin (_{_{}} ω¯t \end{matrix}

+ϕnd)]

(2)

удовлетворение

$_{}^{_{}} \frac{{\overset{}{}}_{}^{}}{{_{_{∑i=1nd'd˜i|2|WRi}} (\overset{jλ)}{}}^{}}$ |2≤1

если и только если _{∥WLTWR∥∞} ≤ 1.

Это приблизительно (очень приблизительно - следующее заявление не на самом деле правильно) подразумевает что _∥WLTWR _∥∞ ≤ 1 если и только если для каждой фиксированной частоты $\overset{ω¯}{}$ , и все синусоидальные беспорядки $\tilde{d}$ формы Уравнение 2 удовлетворения

${\overset{}{}}_{}_{_{|d˜i|≤|WRi}} (\overset{jü)}{}$ |

компоненты ошибки установившегося состояния удовлетворят

${\overset{}{}}_{} \frac{}{_{_{|e˜i|≤1|WLi}} (\overset{jü)}{}}$ |.

Это показывает, как можно выбрать весовые коэффициенты производительности для отражения желаемой частотно-зависимой цели производительности. Используйте _WR для представления относительной величины синусоидальных возмущений, которые могут присутствовать, и используйте _1/WL для представления желаемой верхней границы для последующих ошибок, которые возникают.

Однако помните, что взвешенная норма H∞ фактически не дает поэлементных границ для компонентов $\overset{e˜}{}$ на основе поэлементных границ для компонентов $\overset{d˜}{}$ . Точная граница, которую она дает, в терминах евклидовых норм компонентов $\overset{e˜}{}$ и $\overset{d˜}{}$ (взвешенных соответствующим образом по _WL ( $\overset{jλ}{}$ pw) и WR $\overset{(}{}$ jλ pw)).

См. также

hinfstruct | hinfsyn

Документация