Современный подход к характеристике целей производительности с замкнутым контуром заключается в измерении размера некоторых матриц передаточных функций с замкнутым контуром с использованием различных матричных норм. Матричные нормы обеспечивают меру того, как большие выходные сигналы могут получить для определенных классов входных сигналов. Оптимизация этих типов рабочих характеристик по сравнению с набором стабилизирующих контроллеров является основной тягой современной теории оптимального управления, такой как L1, H2, H∞ и оптимальное управление. Следовательно, важно понять, сколько типов целей управления можно представить как минимизацию функций передачи с замкнутым контуром.
Рассмотрим проблему отслеживания с отклонением возмущений, шумом измерения и ограничениями входного сигнала управления, как показано на обобщенной и взвешенной блок-схеме рабочих характеристик. K - это некоторый контроллер, который должен быть разработан, а G - это система, которой вы хотите управлять.
Типичная цель производительности с замкнутым контуром
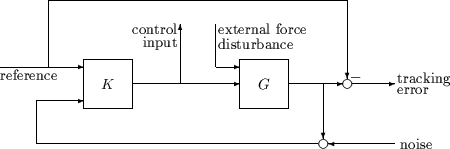
Разумная, хотя и не точная, цель конструкции состояла бы в том, чтобы сконструировать K для сохранения ошибок отслеживания и управления входным сигналом малым для всех разумных опорных команд, шумов датчиков и внешних силовых возмущений.
Следовательно, естественной целью производительности является усиление по замкнутому контуру от внешних воздействий (команды отсчета, шум датчика и внешние силовые возмущения) к регулируемым переменным (ошибки отслеживания и управляющий входной сигнал). В частности, пусть Т обозначает отображение с замкнутым контуром от внешних воздействий к регулируемым переменным:
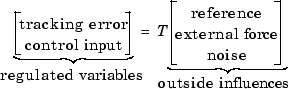
Можно оценить производительность, измерив выигрыш от внешних воздействий к регулируемым переменным. Другими словами, хорошая производительность связана с тем, что Т является небольшим. Поскольку система с замкнутым контуром является динамической системой с множеством входов и множеством выходов (MIMO), существует два различных аспекта усиления T:
Пространственные (векторные возмущения и векторные ошибки)
Временная (динамическая зависимость между входными/выходными сигналами)
Следовательно, критерий эффективности должен учитывать
Относительная величина внешних воздействий
Частотная зависимость сигналов
Относительная важность величин регулируемых переменных
Таким образом, если цель производительности находится в форме матричной нормы, она фактически должна быть взвешенной нормой.
∥WLTWR∥
Цели работы с замкнутым контуром формулируются как взвешенные функции передачи с замкнутым контуром, которые должны быть малы посредством обратной связи. Общий пример, который включает в себя множество релевантных терминов, показан в виде блок-схемы в обобщенной и взвешенной блок-схеме производительности. На диаграмме G обозначает модель установки, а K - контроллер обратной связи.
Обобщенная и взвешенная блок-схема производительности
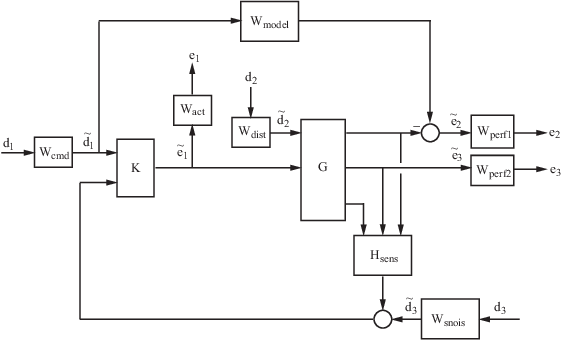
Блоки на этом рисунке могут быть скалярными (SISO) и/или многовариантными (MIMO), в зависимости от конкретного примера. Математическая задача H∞ управления состоит в том, чтобы заставить функцию Ted передачи MIMO с замкнутым контуром удовлетворять ∥Ted∥∞ < 1. Функции взвешивания используются для масштабирования функций передачи ввода/вывода таким образом, что при ∥Ted∥∞ < 1 соотношение между и является подходящим.
Требования к производительности системы с замкнутым контуром преобразуются в H∞ структуру с помощью функций взвешивания или масштабирования. Веса выбираются для учета относительной величины сигналов, их частотной зависимости и их относительной важности. Это отражено на приведенном выше рисунке, где веса или шкалы [Wcmd, Wdist, Wsnois] используются для преобразования и масштабирования нормализованных входных сигналов [d1, d2, d3] в физические единицы, определенные как [d1, d2, d3]. Аналогично веса или шкалы [Wact, Wperf1,Wperf2] преобразуют и масштабируют физические единицы в нормализованные выходные сигналы [e1, e2, e3]. Ниже приводится интерпретация сигналов, функций взвешивания и моделей.
|
Сигнал |
Значение |
|---|---|
|
d1
|
Нормализованная команда привязки Типовая ссылочная команда в физических единицах |
|
d2
|
Нормализованные экзогенные нарушения Типичные экзогенные нарушения в физических единицах |
|
d3
|
Нормализованный шум датчика Типичный шум датчика в физических блоках |
|
e1
|
Взвешенные сигналы управления Фактические сигналы управления в физических блоках |
|
e2
|
Взвешенные ошибки отслеживания Фактические ошибки отслеживания в физических единицах |
|
e3
|
Взвешенные ошибки завода Фактические ошибки завода в физических единицах |
Wcmd
Wcmd входит в проблемы управления H∞, которые требуют отслеживания опорной команды. Wcmd формирует нормализованные опорные командные сигналы (величину и частоту) в действительные (или типичные) опорные сигналы, которые, как ожидается, будут возникать. В нем описывается величина и частотная зависимость опорных команд, генерируемых нормализованным опорным сигналом. Обычно Wcmd плоский на низкой частоте и скатывается на высокой частоте. Например, при решении проблемы управления полетом пилоты истребителя генерируют входные реперные команды до полосы частот около 2 Гц. Предположим, что палка имеет максимальный ход в три дюйма. Команды пилот-сигнала могут быть смоделированы как нормализованные сигналы, проходящие через фильтр первого порядка:
Wmodel
Wmodel представляет собой желаемую идеальную модель для замкнутой системы и часто включается в проблемные рецептуры с требованиями отслеживания. Включение идеальной модели для отслеживания часто называют проблемой сопоставления модели, т.е. целью системы с замкнутым контуром является соответствие определенной модели. Для правильного ответа при отслеживании команд может потребоваться, чтобы система с замкнутым контуром реагировала как хорошо увлажненная система второго порядка. Идеальная модель будет тогда
для конкретной желаемой собственной частоты λ и желаемого коэффициента демпфирования Преобразование единиц может потребоваться для обеспечения точной корреляции между идеальной моделью и системой с замкнутым контуром. В примере пилота истребителя предположим, что командуется скорость крена и требуется отклик 10 °/с для каждого дюйма движения палки. Затем, в этих единицах, соответствующая модель:
»).
Wdist
Wdist формирует частотное содержание и величину экзогенных возмущений, влияющих на растение. Например, рассмотрим электронный микроскоп как растение. Основной задачей является механическая изоляция микроскопа от внешних механических возмущений, таких как возбуждение земли, звуковые (напорные) волны и воздушные токи. Можно захватить спектр и относительные величины этих возмущений с помощью матрицы Wdist взвешивания передаточной функции.
Wperf1
Wperf1 весит разницу между откликом системы с замкнутым контуром и идеальной моделью W. Часто может потребоваться точное согласование идеальной модели на низкой частоте и требуется менее точное согласование на более высокой частоте, в этом случае Wperf1 является плоской на низкой частоте, сворачивается на первом или втором порядке и сглаживается на малом ненулевом значении на высокой частоте. Обратная величина веса связана с допустимым размером ошибок отслеживания при работе с опорными командами и возмущениями, описанными Wcmd и Wdist.
Wperf2
Wperf2 штрафует переменные, внутренние для процесса G, такие как состояния исполнительного механизма, которые являются внутренними для G, или другие переменные, которые не являются частью цели отслеживания.
Wact
Wact используется для формирования штрафа при использовании управляющего сигнала. Wact представляет собой изменяющуюся по частоте взвешивающую функцию, используемую для ограничения пределов отклонения/положения, скорости отклонения/скорости и т.д., реакции управляющих сигналов, когда речь идет о целях отслеживания и отклонения возмущений, определенных выше. Каждый управляющий сигнал обычно наказывается независимо.
Wsnois
Wsnois представляет модели частотной области шума датчика. Каждая обратная связь датчика с контроллером имеет некоторый шум, который часто выше в одном диапазоне частот, чем в другом. Вес Wsnois пытается зафиксировать эту информацию, полученную из лабораторных экспериментов или на основе измерений производителя, в проблеме контроля. Например, акселерометры среднего класса имеют значительный шум при низкой частоте и высокой частоте. Поэтому соответствующий вес Wsnois будет больше при низкой и высокой частоте и будет иметь меньшую величину в диапазоне средних частот. Измерение смещения или вращения часто является довольно точным при низкой частоте и в устойчивом состоянии, но реагирует плохо по мере увеличения частоты. Функция взвешивания для этого датчика будет небольшой на низкой частоте, постепенно возрастет в качестве системы первого или второго порядка и выровняется на высокой частоте.
Hsens
Hsens представляет модель динамики датчика или внешний сглаживающий фильтр. Функции переноса, используемые для описания Hsens, основаны на физических характеристиках отдельных компонентов. Эти модели также могут быть включены в модель G.
Эта общая блок-схема обладает огромной гибкостью, и многие цели эффективности управления могут быть сформулированы в структуре H∞ с использованием этого описания блок-схемы.
Компромиссы между производительностью и надежностью в конструкции управления обсуждались в контексте формирования цикла с несколькими переменными в разделе Компромисс между производительностью и надежностью. В структуру управления H∞ можно включить цели надежности в качестве дополнительного возмущения для функций передачи ошибок - возмущения должны оставаться небольшими. Рассмотрим следующий рисунок системы обратной связи с замкнутым контуром с аддитивными и мультипликативными моделями неопределенности.
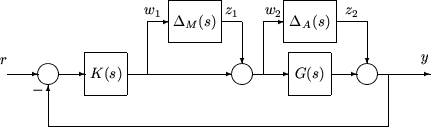
Матрицы передаточных функций определяются как:
(s) = K (I + GK) − 1
где TI (s) обозначает входную дополняющую функцию чувствительности, а SO (s) обозначает выходную функцию чувствительности. Ограничения на размер матриц передаточной функции от z1 до w1 и от z2 до w2 обеспечивают устойчивость системы с замкнутым контуром к мультипликативной неопределенности ΔM (s) на входе установки и аддитивной неопределенности ΔA (s) вокруг установки G (s). В формулировке проблемы управления H∞ цели надежности входят в процедуру синтеза в качестве дополнительных входных/выходных сигналов, которые должны оставаться малыми. Соединение с удаленными блоками неопределенности следует ниже.
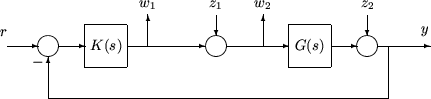
Задача обеспечения надежности управления H∞ теперь имеет тот же формат, что и цели производительности, т.е. сводит к минимуму H∞ норму матрицы переноса от z, [z1, z2], до w, [w1, w2].
Матрицы взвешивания или масштабирования часто вводятся для формирования частотного и амплитудного содержания матриц чувствительности и комплементарной функции передачи чувствительности. Пусть WM соответствует мультипликативной неопределенности, а WA соответствует аддитивной модели неопределенности. ΔM (s) и ΔA (s) считаются нормой, ограниченной 1, т.е. | ΔM (s) | < 1 и | ΔA (s) | < 1. Следовательно, в зависимости от частоты, | WM (jλ) | и | WA (jλ) | являются соответствующими размерами наибольших ожидаемых аддитивных и мультипликативных возмущений растений.
Мультипликативное взвешивание или масштабирование WM представляет собой процентную ошибку в модели и часто является небольшой по величине при низкой частоте, от 0,05 до 0,20 (ошибка моделирования от 5% до 20%) и увеличивается по величине при высокой частоте, от 2 до 5 ((ошибка моделирования от 200% до 500%). Вес будет переходить, пересекая величину 1, что соответствует 100% неопределенности в модели, с частотой, по меньшей мере, в два раза превышающей ширину полосы системы с замкнутым контуром. Типичным мультипликативным весом является
11200s + 1.
Напротив, аддитивный вес или масштабирование WA представляет абсолютную ошибку, которая часто мала при низкой частоте и велика по величине при высокой частоте. Величина этого веса напрямую зависит от величины модели растения G (s).
Не выбирайте функции взвешивания с полюсами, очень близкими к s = 0 (z = 1 для дискретно-временных систем). Например, хотя может показаться разумным выбрать Wcmd = 1/s, чтобы принудить нулевую ошибку установившегося состояния, это приводит к нестабильному полюсу, который не может быть стабилизирован, вызывая сбой синтеза. Вместо этого выберите Wcmd = 1/( s + δ). Значение δ должно быть малым, но не очень малым по сравнению с динамикой системы. Например, для наилучших числовых результатов, если целевая частота пересечения составляет около 1 рад/с, выберите δ = 0,0001 или 0,001. Аналогично, в дискретное время выбирайте время выборки таким образом, чтобы динамика системы и взвешивания была не более чем на десятилетие или два ниже частоты Найквиста.
hinfstruct | hinfsyn | mixsyn