Формирование контура смешанной чувствительности позволяет разработать контроллер H∞, одновременно формируя частотные характеристики для отслеживания и отклонения возмущений, снижения шума и надежности, а также усилия контроллера. Этот метод является полезным способом сбалансировать необходимый компромисс между производительностью и надежностью. Чтобы использовать этот метод, вы преобразуете желаемые ответы в до трех весовых функций, которые mixsyn используется для синтеза контроллера.
mixsyn проектирует контроллер K для вашего завода G, предполагая стандартную конфигурацию управления на следующей схеме.
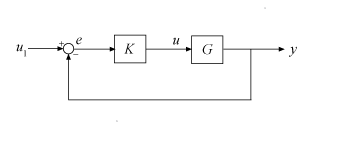
Для этого функция добавляет к системе управления предоставляемые функции взвешивания, W1 (ы), W2 (ы) и W3 (ы), как показано на следующей диаграмме.
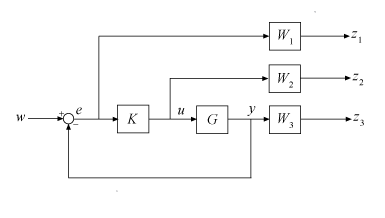
mixsyn рассматривает проблему как задачу синтеза H∞ (см. hinfsyn). Он анализирует взвешенную систему управления как LFT (P, K), где P является усиленной установкой P, так что {z; e} = P {w; u}, как показано на следующей диаграмме.
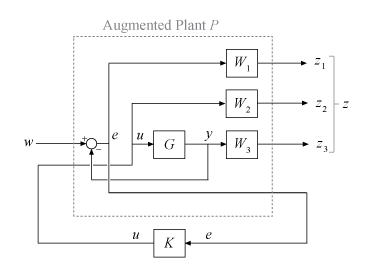
Передаточная функция от w до z может быть выражена как
W1SW2KSW3T],
где
S = (I + GK) -1 - функция чувствительности.
KS - передаточная функция от w до u (усилие управления).
T = (I - S) = GK (I + GK) -1 - функция комплементарной чувствительности.
mixsyn ищет контроллер K, который минимизирует | | M (s) ||∞, H∞ норму (пиковое усиление) M. Для этого он вызываетhinfsyn на дополненном растении P = augw(G,W1,W2,W3).
Для усиления контура L = GK для достижения хорошего опорного трекинга и отклонения возмущений обычно требуется высокое усиление контура на низкой частоте. Для достижения устойчивости и ослабления шума измерений обычно требуется, чтобы L скатывался на высокой частоте. Эта форма контура эквивалентна малой S на низкой частоте и малой T на высокой частоте.
Для формирования цикла смешанной чувствительности выбираются функции взвешивания для определения этих целевых форм для S и T, а также контрольных усилий KS. Проектное ограничение H∞,
‖ ∞≤ 1,
означает, что
.
Поэтому для S, KS и T. веса задаются равными взаимным значениям требуемых форм. В частности,
Для хорошего эталонного отслеживания и отклонения возмущений выберите W1 большой внутри полосы пропускания управления, чтобы получить малый S.
Для обеспечения надежности и ослабления шума выберите W3 большие за пределами полосы управления для получения малых T.
Чтобы ограничить усилия управления в конкретной полосе частот, увеличьте величину W2 в этой полосе частот, чтобы получить малую КС.
mixsyn возвращает минимальное значение | | M, ||∞ в выходном аргументеgamma. Для возвращенного контроллера К
.
Если ограничение усилий по управлению не требуется, W2 можно опустить. В этом случае mixsyn минимизирует H∞ норму
W1SW3T].
Вы можете использовать makeweight для создания функций взвешивания с требуемыми профилями усиления. В следующем примере показано, как выбрать и создать функции взвешивания для проектирования контроллера с помощью mixsyn.
Не выбирайте функции взвешивания с полюсами, очень близкими к s = 0 (z = 1 для дискретно-временных систем). Например, хотя может показаться разумным выбрать W1 = 1/с, чтобы принудить нулевую ошибку установившегося состояния, это вводит неустойчивый полюс, который не может быть стабилизирован, вызывая сбой синтеза. Вместо этого выберите W1 = 1/( s + δ). Значение δ должно быть малым, но не очень малым по сравнению с динамикой системы. Например, для наилучших числовых результатов, если целевая частота пересечения составляет около 1 рад/с, выберите δ = 0,0001 или 0,001. Аналогично, в дискретное время выбирайте время выборки таким образом, чтобы динамика системы и взвешивания была не более чем на десятилетие или два ниже частоты Найквиста.
Загрузите модель установки для конструкции контроллера mixed-sensitivityH∞. Эта модель с двумя входами и двумя выходами в шести состояниях описана в примере формирования контура контроллера оси шага HIMAT.
load mixsynExampleData G size(G)
State-space model with 2 outputs, 2 inputs, and 6 states.
Разработать контроллер для обеспечения производительности и надежности, сформировать функции чувствительности и дополнительной чувствительности. Выберите веса, которые являются обратными желаемым фигурам.
Для достижения хороших характеристик отслеживания и отклонения помех форма S должна быть небольшой внутри полосы пропускания управления, что означает выбор W1 большая на низкой частоте, откатывающаяся на высокой частоте. В этом примере укажите W1 с:
Низкочастотный коэффициент усиления около 30 дБ (33 в абсолютных единицах)
Высокочастотный коэффициент усиления около -6 дБ (0,5 в абсолютных единицах)
0 дБ кроссовера со скоростью около 5 рад/с.
W1 = makeweight(33,5,0.5);
Для устойчивости и ослабления шума, форма T чтобы быть маленьким за пределами полосы пропускания управления, что означает выбор W3 большая на высокой частоте.
W3 = makeweight(0.5,20,20);
Проверьте обе функции взвешивания. Их обратные значения являются целевыми фигурами для S и T.
bodemag(W1,W3) yline(0,'--'); legend('W1','W3','0 dB') grid on

Поскольку S + T = I, mixsyn не может сделать оба S и T малый (менее 0 дБ) в том же диапазоне частот. Поэтому при указании весов должна существовать полоса частот, в которой оба W1 и W3 ниже 0 дБ.
Использовать mixsyn для вычисления оптимального контроллера смешанной чувствительности с этими весами. В этом примере установка не налагает никаких штрафов на усилия контроллера W2 кому [].
[K,CL,gamma] = mixsyn(G,W1,[],W3); gamma
gamma = 0.7331
Получающееся gamma, которое является пиковым сингулярным значением для всех частот, значительно ниже 1, что указывает на то, что система с замкнутым контуром соответствует проектным требованиям. Проверьте полученные системные ответы. Сначала сравните результирующую чувствительность S и дополнительная чувствительность T к соответствующим функциям взвешивания W1 и W3.
L = G*K; I = eye(size(L)); S = feedback(I,L); T= I-S; sigma(S,'b',W1,'b--',T,'r',W3,'r--',{0.1,1000}) legend('S','W1','T','W3')

Сюжет показывает, что S и T достичь желаемой формы петли, где S велика внутри полосы пропускания управления и а мала вне полосы пропускания управления.
Чтобы увидеть, как формирование цикла смешанной чувствительности достигает целей классического формирования цикла, сравните отклик разомкнутого цикла. L к функциям взвешивания. L ~ W1 где W1 большой, и L ~ 1/W3 где W3 большой.
sigma(L,'b',W1,'r--',1/W3,'g--',{0.1,1000}) legend('L','W1','1/W3')
