Односторонний анализ отклонений
p = anova1(y)y и возвращает значение p. anova1 обрабатывает каждый столбец y в виде отдельной группы. Функция проверяет гипотезу о том, что выборки в столбцах y взяты из популяций с тем же средним значением против альтернативной гипотезы, что популяционные средства не все одинаковы. Функция также отображает рамочный график для каждой группы в y и стандартная таблица ANOVA (tbl).
p = anova1(y,group,displayopt)displayopt является 'on' (по умолчанию) и подавляет отображение, когда displayopt является 'off'.
[ возвращает таблицу ANOVA (включая метки столбцов и строк) в массиве ячеек p,tbl] = anova1(___)tbl используя любую из комбинаций входных аргументов в предыдущих синтаксисах. Чтобы скопировать текстовую версию таблицы ANOVA в буфер обмена, выберите команду «Редактирование» > «Копировать текст» на рисунке таблицы ANOVA.
[ возвращает структуру, p,tbl,stats] = anova1(___)stats, который можно использовать для выполнения нескольких сравнительных тестов. Множественный тест сравнения позволяет определить, какие пары групповых средств значительно отличаются. Для выполнения этого теста используйте multcompare, предоставление stats структура в качестве входного аргумента.
Создание матрицы данных образца y со столбцами, которые являются константами, плюс случайные нормальные возмущения со средним значением 0 и стандартным отклонением 1.
y = meshgrid(1:5); rng default; % For reproducibility y = y + normrnd(0,1,5,5)
y = 5×5
1.5377 0.6923 1.6501 3.7950 5.6715
2.8339 1.5664 6.0349 3.8759 3.7925
-1.2588 2.3426 3.7254 5.4897 5.7172
1.8622 5.5784 2.9369 5.4090 6.6302
1.3188 4.7694 3.7147 5.4172 5.4889
Выполнить одностороннюю ANOVA.
p = anova1(y)


p = 0.0023
Таблица ANOVA показывает вариацию между группами (Columns) и изменение внутри групп (Error). SS - сумма квадратов, и df - степени свободы. Суммарные степени свободы - общее количество наблюдений минус один, что составляет 25 - 1 = 24. Степенями свободы между группами является число групп минус одна, что равно 5 - 1 = 4. Степени свободы внутри групп - это суммарные степени свободы минус степени свободы между группами, которые равны 24 - 4 = 20.
MS - среднеквадратичная ошибка, которая SS/df для каждого источника изменения. F-статистика представляет собой отношение среднеквадратичных ошибок (13.4309/2.2204). Значение p - это вероятность того, что статистика теста может принять значение, большее, чем значение вычисленной статистики теста, т.е. P (F > 6,05). Малое значение p 0,0023 указывает на то, что различия между столбцами значительны.
Введите данные образца.
strength = [82 86 79 83 84 85 86 87 74 82 ... 78 75 76 77 79 79 77 78 82 79]; alloy = {'st','st','st','st','st','st','st','st',... 'al1','al1','al1','al1','al1','al1',... 'al2','al2','al2','al2','al2','al2'};
Данные взяты из исследования прочности несущих балок в Хогге (1987). Сила вектора измеряет прогибы пучков в тысячных долях дюйма под 3000 фунтов силы. Векторный сплав идентифицирует каждую балку как сталь ('st'), сплав 1 ('al1'), или сплав 2 ('al2'). Хотя сплав сортируется в этом примере, группирование переменных не требуется.
Проверить нулевую гипотезу о том, что стальные балки по прочности равны балкам, изготовленным из двух более дорогих сплавов. Выключите отображение рисунка и верните результаты ANOVA в массив ячеек.
[p,tbl] = anova1(strength,alloy,'off')p = 1.5264e-04
tbl=4×6 cell array
Columns 1 through 5
{'Source'} {'SS' } {'df'} {'MS' } {'F' }
{'Groups'} {[184.8000]} {[ 2]} {[ 92.4000]} {[ 15.4000]}
{'Error' } {[102.0000]} {[17]} {[ 6.0000]} {0x0 double}
{'Total' } {[286.8000]} {[19]} {0x0 double} {0x0 double}
Column 6
{'Prob>F' }
{[1.5264e-04]}
{0x0 double }
{0x0 double }
Суммарные степени свободы - общее количество наблюдений минус один, что равно 19. Степенями свободы между группами является число групп минус одна, что равно = 2. Степени свободы внутри групп - это суммарные степени свободы минус степени свободы между группами, что = 17.
MS - среднеквадратичная ошибка, которая SS/df для каждого источника изменения. F-статистика - это отношение среднеквадратичных ошибок. Значение p - это вероятность того, что статистика теста может принимать значение, большее или равное значению статистики теста. P-значение 1.5264e-04 предполагает отказ от нулевой гипотезы.
Можно получить значения в таблице ANOVA, проиндексировав их в массив ячеек. Сохранение значения F-статистики и значения p в новых переменных Fstat и pvalue.
Fstat = tbl{2,5}Fstat = 15.4000
pvalue = tbl{2,6}pvalue = 1.5264e-04
Введите данные образца.
strength = [82 86 79 83 84 85 86 87 74 82 ... 78 75 76 77 79 79 77 78 82 79]; alloy = {'st','st','st','st','st','st','st','st',... 'al1','al1','al1','al1','al1','al1',... 'al2','al2','al2','al2','al2','al2'};
Данные взяты из исследования прочности несущих балок в Хогге (1987). Сила вектора измеряет прогибы пучков в тысячных долях дюйма под 3000 фунтов силы. Векторный сплав идентифицирует каждую балку как сталь (st), сплав 1 (al1), или сплав 2 (al2). Хотя сплав сортируется в этом примере, группирование переменных не требуется.
Выполнение одностороннего ANOVA с использованием anova1. Возврат структуры stats, который содержит статистику multcompare требуется для выполнения нескольких сравнений.
[~,~,stats] = anova1(strength,alloy);


Малое значение p 0,0002 предполагает, что прочность пучков не одинакова.
Выполните многократное сравнение средней прочности балок.
[c,~,~,gnames] = multcompare(stats);

Просмотрите результаты сравнения с соответствующими именами групп.
[gnames(c(:,1)), gnames(c(:,2)), num2cell(c(:,3:6))]
ans=3×6 cell array
Columns 1 through 5
{'st' } {'al1'} {[ 3.6064]} {[ 7]} {[10.3936]}
{'st' } {'al2'} {[ 1.6064]} {[ 5]} {[ 8.3936]}
{'al1'} {'al2'} {[-5.6280]} {[-2]} {[ 1.6280]}
Column 6
{[1.6831e-04]}
{[ 0.0040]}
{[ 0.3560]}
Первые два столбца показывают пару сравниваемых групп. В четвертом столбце показана разница между оцененными значениями группы. Третий и пятый столбцы показывают нижний и верхний пределы для 95% доверительных интервалов истинной разницы средств. Шестой столбец показывает p-значение для гипотезы, что истинная разность средств для соответствующих групп равна нулю.
Первые две строки показывают, что оба сравнения с участием первой группы (стали) имеют доверительные интервалы, которые не включают ноль. Поскольку соответствующие значения p (1,6831e-04 и 0,0040 соответственно) малы, эти различия являются значительными.
Третий ряд показывает, что различия в прочности между двумя сплавами незначительны. 95% доверительный интервал для разницы составляет [-5,6,1.6], поэтому нельзя отвергнуть гипотезу о том, что истинная разница равна нулю. Соответствующее значение p 0,3560 в шестом столбце подтверждает этот результат.
На чертеже синяя полоса представляет интервал сравнения средней прочности материала для стали. Красные полосы представляют интервалы сравнения средней прочности материала для сплава 1 и сплава 2. Ни один из красных стержней не перекрывается с синим стержнем, что указывает на то, что средняя прочность материала для стали значительно отличается от средней прочности материала сплава 1 и сплава 2. Чтобы подтвердить значительную разницу, щелкните на стержнях, представляющих сплав 1 и 2.
y - выборочные данныеОбразец данных, указанный как вектор или матрица.
Если y является вектором, необходимо указать group входной аргумент. Каждый элемент в group представляет имя группы соответствующего элемента в y. anova1 функция обрабатывает y значения, соответствующие одному и тому же значению group в составе той же группы. Эта конструкция используется, когда группы имеют разное количество элементов (несбалансированная ANOVA).
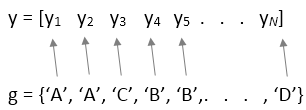
Если y является матрицей и не указывается group, то anova1 обрабатывает каждый столбец y в виде отдельной группы. В этой конструкции функция оценивает, равны ли средства заполнения столбцов. Используйте эту конструкцию, когда каждая группа имеет одинаковое количество элементов (сбалансированная ANOVA).
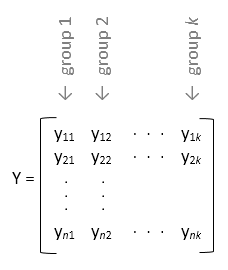
Если y является матрицей и указывается group, затем каждый элемент в group представляет имя группы для соответствующего столбца в y. anova1 функция обрабатывает столбцы, имеющие одно и то же имя группы, как часть одной и той же группы.
Примечание
anova1 игнорирует любое NaN значения в y. Также, если group содержит пустое или NaN значения, anova1 игнорирует соответствующие наблюдения в y. anova1 функция выполняет сбалансированную ANOVA, если каждая группа имеет одинаковое количество наблюдений после того, как функция игнорирует пустые или NaN значения. В противном случае anova1 выполняет несбалансированную ANOVA.
Типы данных: single | double
group - Группирующая переменнаяПеременная группировки, содержащая имена групп, заданная как числовой вектор, логический вектор, категориальный вектор, символьный массив, строковый массив или массив ячеек символьных векторов.
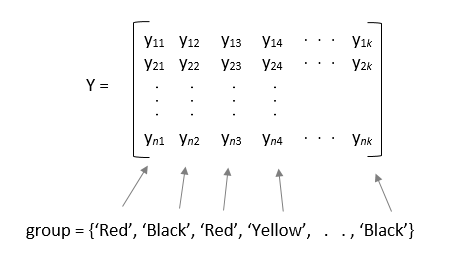
Если y является вектором, то каждый элемент в group представляет имя группы соответствующего элемента в y. anova1 функция обрабатывает y значения, соответствующие одному и тому же значению group в составе той же группы.
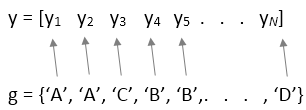
N - общее число наблюдений.
Если y является матрицей, затем каждый элемент в group представляет имя группы для соответствующего столбца в y. anova1 функция обрабатывает столбцы y , которые имеют одно и то же имя группы в составе одной и той же группы.

Если не требуется указывать имена групп для матричных данных выборки y, введите пустой массив ([]) или опустить этот аргумент. В этом случае anova1 обрабатывает каждый столбец y в виде отдельной группы.
Если group содержит пустое или NaN значения, anova1 игнорирует соответствующие наблюдения в y.
Дополнительные сведения о группировании переменных см. в разделе Группирование переменных.
Пример: 'group',[1,2,1,3,1,...,3,1] когда y является вектором с наблюдениями, разделенными на группы 1, 2 и 3
Пример: 'group',{'white','red','white','black','red'} когда y - матрица с пятью столбцами, разделенными на группы: красный, белый и черный
Типы данных: single | double | logical | categorical | char | string | cell
displayopt - Индикатор для отображения таблицы ANOVA и рамочного графика'on' (по умолчанию) | 'off'Индикатор отображения таблицы ANOVA и рамочного графика, указанный как 'on' или 'off'. Когда displayopt является 'off', anova1 возвращает только выходные аргументы. Он не отображает стандартную таблицу ANOVA и рамочный график.
Пример: p = anova(x,group,'off')
p - значение p для F-тестаp-значение для F-теста, возвращаемое как скалярное значение. p-значение - вероятность того, что F-статистика может принять значение, большее, чем вычисленное значение test-statistic. anova1 проверяет нулевую гипотезу о том, что все групповые средства равны друг другу, против альтернативной гипотезы о том, что по меньшей мере одно групповое средство отличается от других. Функция извлекает значение p из cdf F-распределения.
Значение p, которое меньше уровня значимости, указывает, что, по меньшей мере, одно из средств выборки значительно отличается от других. Общие уровни значимости составляют 0,05 или 0,01.
tbl - таблица ANOVAтаблица ANOVA, возвращенная в виде массива ячеек. tbl имеет шесть столбцов.
| Колонка | Определение |
|---|---|
source | Источник изменчивости. |
SS | Сумма квадратов для каждого источника. |
df | Степени свободы, связанные с каждым источником. Предположим, что N - общее число наблюдений, а k - число групп. Затем N - k - внутригрупповые степени свободы (Error), k - 1 - межгрупповые степени свободы (Columns), а N - 1 - суммарные степени свободы. N - 1 = (N - k) + (k - 1) |
MS | Среднее значение квадратов для каждого источника, которое является отношением SS/df. |
F | F-статистика, которая является отношением средних квадратов. |
Prob>F | Значение p, которое является вероятностью того, что F-статистика может принять значение, большее, чем вычисленное значение test-statistic. anova1 выводит эту вероятность из cdF-распределения. |
Строки таблицы ANOVA показывают изменчивость данных, разделенных источником.
| Ряд | Определение |
|---|---|
Groups | Изменчивость из-за различий между групповыми средами (изменчивость между группами) |
Error | Изменчивость из-за различий между данными в каждой группе и средним значением группы (изменчивость в группах) |
Total | Общая изменчивость |
stats - Статистика для нескольких сравнительных тестовСтатистика для нескольких тестов сравнения, возвращенная в виде структуры с полями, описанными в этой таблице.
| Имя поля | Определение |
|---|---|
gnames | Названия групп |
n | Количество наблюдений в каждой группе |
source | Источник stats продукция |
means | Оценочные значения средств |
df | Погрешность (внутри групп) степеней свободы (N - k, где N - общее число наблюдений, а k - число групп) |
s | Квадратный корень среднеквадратической ошибки |
anova1 возвращает график полей наблюдений для каждой группы в y. Прямоугольные графики обеспечивают визуальное сравнение параметров расположения группы.
На каждой рамке центральной отметкой является медиана (2-й квантиль, q2), а краями рамки являются 25-й и 75-й процентили (1-й и 3-й квантили, q1 и q3 соответственно). Усы распространяются на самые экстремальные точки данных, которые не считаются отклонениями. Отклонения строятся по отдельности с помощью '+' символ. Крайности усов соответствуют q3 + 1,5 × (q3 - q1) и q1 - 1,5 × (q3 - q1).
Прямоугольные графики включают вырезы для сравнения средних значений. Два медиана значительно различаются на уровне значимости 5%, если их интервалы, представленные выемками, не перекрываются. Этот тест отличается от F-теста, который выполняет ANOVA; однако большие различия в центральных линиях полей соответствуют большому F-статистическому значению и соответственно малому p-значению. Крайности выемок соответствуют q2 - 1,57 (q3 - q1 )/sqrt (n) и q2 + 1,57 (q3 - q1 )/sqrt (n), где n - число наблюдений без каких-либоNaN значения.
Дополнительные сведения о оконных графиках см. в разделе 'Whisker' и 'Notch' из boxplot.
[1] Хогг, Р. В. и Дж. Ледольтер. Инженерная статистика. Нью-Йорк: Макмиллан, 1987.
anova2 | anovan | boxplot | multcompare
Имеется измененная версия этого примера. Открыть этот пример с помощью изменений?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.