Односторонняя АНОВА

Введение в одностороннюю ANOVA

Можно использовать функцию anova1 для выполнения одностороннего анализа дисперсии (ANOVA). Целью односторонней ANOVA является определение того, имеют ли данные из нескольких групп (уровней) фактора общее среднее значение. То есть односторонняя ANOVA позволяет выяснить, оказывают ли различные группы независимой переменной различное влияние на переменную ответа y. Предположим, больница хочет определить, сокращают ли два новых предлагаемых метода планирования время ожидания пациента больше, чем старый способ планирования встреч. В этом случае независимой переменной является метод планирования, а переменной ответа - время ожидания пациентов.

Односторонняя ANOVA - простой частный случай линейной модели. Односторонняя форма модели ANOVA

$_{yij} =_{} {αj}_{+}$ αij

со следующими допущениями:

yij - это наблюдение, в котором i представляет номер наблюдения, а j представляет другую группу (уровень) переменной y. Все yij независимы.
αj представляет собой среднее население для j-й группы (уровень или лечение).
αij - случайная ошибка, независимая и нормально распределенная, с нулевой средней и постоянной дисперсией, то есть αij ~ N (0, start2).

Эта модель также называется моделью средств. Модель предполагает, что столбцами y являются константа αj плюс составляющая ошибки αij. ANOVA помогает определить, все ли константы одинаковы.

ANOVA проверяет гипотезу о том, что все групповые средства равны ( $_{H0} :_{} α1_{=} α2 = ._{.}$ . = αk) против альтернативной гипотезы о том, что по крайней мере одна группа отличается от $_{} {других}_{} (_{}$ H1:αi≠αj по крайней мере для одного i и j).anova1(y) проверяет равенство значений столбцов для данных в матрице y, где каждый столбец является отдельной группой и имеет одинаковое количество наблюдений (т.е. сбалансированный дизайн). anova1(y,group) проверяет равенство групповых средств, указанных в group, для данных в векторе или матрице y. В этом случае каждая группа или столбец может иметь различное количество наблюдений (т.е. несбалансированную конструкцию).

ANOVA основана на предположении, что все выборочные популяции обычно распределены. Известно, что она устойчива к скромным нарушениям этого предположения. Можно визуально проверить предположение о нормальности, используя график нормальности (normplot). Кроме того, можно использовать одну из функций Toolbox™ статистики и машинного обучения, которая проверяет нормальность: тест Андерсона-Дарлинга (adtest), хи-квадрат благости теста подгонки (chi2gof), тест Жарке-Бера (jbtest) или тест Лиллиефорса (lillietest).

Подготовка данных для односторонней ANOVA

Можно предоставить данные образца в виде вектора или матрицы.

Если данные выборки находятся в векторе, y, то необходимо предоставить информацию о группировке с помощью group входная переменная: anova1(y,group).
group должен быть числовым вектором, логическим вектором, категориальным вектором, символьным массивом, строковым массивом или массивом ячеек символьных векторов, с одним именем для каждого элемента y. anova1 функция обрабатывает y значения, соответствующие одному и тому же значению group в составе той же группы. Например,

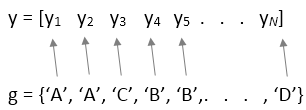
Эта конструкция используется, когда группы имеют разное количество элементов (несбалансированная ANOVA).
Если данные выборки находятся в матрице, y, предоставление информации о группе является необязательным.
- Если входная переменная не указана group, то anova1 обрабатывает каждый столбец y как отдельная группа, и оценивает, равны ли средства заполнения столбцов. Например,
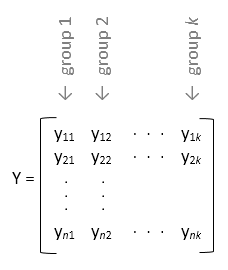
  Используйте эту форму проектирования, когда каждая группа имеет одинаковое количество элементов (сбалансированная ANOVA).
- При указании входной переменной group, затем каждый элемент в group представляет имя группы для соответствующего столбца в y. anova1 обрабатывает столбцы с тем же именем группы как часть той же группы. Например,

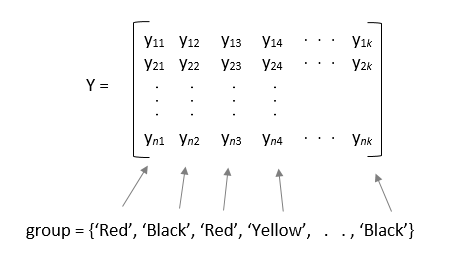
anova1 игнорирует любое NaN значения в y. Также, если group содержит пустое или NaN значения, anova1 игнорирует соответствующие наблюдения в y. anova1 функция выполняет сбалансированную ANOVA, если каждая группа имеет одинаковое количество наблюдений после того, как функция игнорирует пустые или NaN значения. В противном случае anova1 выполняет несбалансированную ANOVA.

Выполнить одностороннюю ANOVA

Открыть сценарий в реальном времени

В этом примере показано, как выполнить одностороннюю ANOVA, чтобы определить, имеют ли данные из нескольких групп общее среднее значение.

Загрузите и просмотрите данные образца.

load hogg
hogg

hogg = 6×5

    24    14    11     7    19
    15     7     9     7    24
    21    12     7     4    19
    27    17    13     7    15
    33    14    12    12    10
    23    16    18    18    20

Данные получены из исследования Hogg and Ledolter (1987) о количестве бактерий в поставках молока. Столбцы матрицы hogg представляют различные транспортировки. Ряды - это количество бактерий из коробок молока, выбранных случайным образом из каждой партии.

Проверьте, имеют ли некоторые поставки большее количество, чем другие. По умолчанию anova1 возвращает две цифры. Одна из них является стандартной таблицей ANOVA, а другая - покадровыми графиками данных по группам.

[p,tbl,stats] = anova1(hogg);

Figure One-way ANOVA contains objects of type uicontrol.

Figure contains an axes. The axes contains 35 objects of type line.

p = 1.1971e-04

Небольшое значение p, равное примерно 0,0001, указывает на то, что количество бактерий из различных партий не является одинаковым.

Вы можете получить некоторую графическую уверенность в том, что средства различны, посмотрев на прямоугольные графики. Насечки, однако, сравнивают медианы, а не средства. Дополнительные сведения об этом дисплее см. в разделе boxplot.

Просмотрите стандартную таблицу ANOVA. anova1 сохраняет стандартную таблицу ANOVA в качестве массива ячеек в выходном аргументе tbl.

tbl

tbl=4×6 cell array
  Columns 1 through 5

    {'Source' }    {'SS'        }    {'df'}    {'MS'      }    {'F'       }
    {'Columns'}    {[  803.0000]}    {[ 4]}    {[200.7500]}    {[  9.0076]}
    {'Error'  }    {[  557.1667]}    {[25]}    {[ 22.2867]}    {0x0 double}
    {'Total'  }    {[1.3602e+03]}    {[29]}    {0x0 double}    {0x0 double}

  Column 6

    {'Prob>F'    }
    {[1.1971e-04]}
    {0x0 double  }
    {0x0 double  }

Сохранение значения F-статистики в переменной Fstat.

Fstat = tbl{2,5}

Fstat = 9.0076

Просмотрите статистику, необходимую для многократного попарного сравнения групповых средств. anova1 сохраняет эти статистические данные в структуре stats.

stats

stats = struct with fields:
    gnames: [5x1 char]
         n: [6 6 6 6 6]
    source: 'anova1'
     means: [23.8333 13.3333 11.6667 9.1667 17.8333]
        df: 25
         s: 4.7209

ANOVA отвергает нулевую гипотезу о том, что все групповые средства равны, поэтому можно использовать множественные сравнения, чтобы определить, какие групповые средства отличаются от других. Для выполнения нескольких тестов сравнения используйте функцию multcompare, которая принимает stats в качестве входного аргумента. В этом примере: anova1 отвергает нулевую гипотезу о том, что среднее количество бактерий из всех четырех партий равно друг другу, то есть $_{H0} :_{} мк1_{=}_{мк2} =_{}$ мк3 = мк4.

Выполните множественный сравнительный тест, чтобы определить, какие поставки отличаются от других с точки зрения среднего количества бактерий.

multcompare(stats)

Figure Multiple comparison of means contains an axes. The axes with title Click on the group you want to test contains 11 objects of type line.

ans = 10×6

    1.0000    2.0000    2.4953   10.5000   18.5047    0.0059
    1.0000    3.0000    4.1619   12.1667   20.1714    0.0013
    1.0000    4.0000    6.6619   14.6667   22.6714    0.0001
    1.0000    5.0000   -2.0047    6.0000   14.0047    0.2119
    2.0000    3.0000   -6.3381    1.6667    9.6714    0.9719
    2.0000    4.0000   -3.8381    4.1667   12.1714    0.5544
    2.0000    5.0000  -12.5047   -4.5000    3.5047    0.4806
    3.0000    4.0000   -5.5047    2.5000   10.5047    0.8876
    3.0000    5.0000  -14.1714   -6.1667    1.8381    0.1905
    4.0000    5.0000  -16.6714   -8.6667   -0.6619    0.0292

Первые два столбца показывают, какие групповые средства сравниваются друг с другом. Например, в первой строке сравниваются средства для групп 1 и 2. В последнем столбце показаны значения p для тестов. Значения p 0,0059, 0,0013 и 0,0001 указывают на то, что среднее количество бактерий в молоке из первой партии отличается от количества бактерий из второй, третьей и четвертой партий. Значение p 0,0292 указывает на то, что среднее количество бактерий в молоке из четвертой партии отличается от количества бактерий из пятой партии. Процедура не отвергает гипотезы о том, что другие групповые средства отличаются друг от друга.

На рисунке также показан тот же результат. Синяя полоса показывает интервал сравнения для среднего значения первой группы, который не перекрывается с интервалами сравнения для средств второй, третьей и четвертой группы, показанными красным цветом. Интервал сравнения для среднего значения пятой группы, показанного серым цветом, перекрывается с интервалом сравнения для среднего значения первой группы. Следовательно, групповые средства для первой и пятой групп существенно не отличаются друг от друга.

Математические детали

ANOVA проверяет разницу в групповых значениях путем разделения общей вариации данных на два компонента:

Изменение групповых значений от общего среднего значения, то есть ${\overset{}{y _}}_{j} {\overset{}{}}_{−}$ y _ w.. (вариация между группами), ${\overset{}{}}_{где}$ y - среднее значение выборки для группы ${\overset{,}{j}}_{}$ и y - - общее среднее значение выборки.
Вариация наблюдений в каждой группе от их групповых средних оценок, $_{yij} {\overset{}{-}}_{y}$ bet.j (вариация внутри группы).

Другими словами, ANOVA разбивает общую сумму квадратов (SST) на сумму квадратов из-за эффекта между группами (SSR) и сумму ошибок квадратов (SSE).

$\underset{.)}{\underset{.}{\underset{}{} \underset{∑i∑j}{} {(_{} yij {\bar{}}_{y}}^{pw}}} \underline{\underset{}{\underset{}{}_{} {\overset{}{}}_{2︸SST=∑jnj} {\overset{y}{(}}_{su.j}^{}}} y \underset{(}{\underset{2︸SSR+\sumi\sumj}{\underset{bw}{} \underset{.}{.} {)_{} {\overset{}{}}_{}}^{}}}$ yij − y bet.j) 2︸SSE,

где _nj - размер выборки для j-ой группы, j = 1, 2,..., k.

Затем ANOVA сравнивает вариацию между группами с вариацией внутри групп. Если отношение межгрупповой вариации к внутригрупповой вариации значительно высокое, то можно сделать вывод, что групповые средства значительно отличаются друг от друга. Вы можете измерить это с помощью статистики теста, которая имеет F-распределение со степенями свободы (k-1, N-k):

$F \frac{\frac{=}{SSRk}}{\frac{-}{}} \frac{1SSEN -}{k} =_{MSRMSE} ~$ Fk − 1, N − k,

где MSR - среднеквадратичная обработка, MSE - среднеквадратичная ошибка, k - число групп, а N - общее число наблюдений. Если p-значение для F-статистики меньше уровня значимости, то тест отвергает нулевую гипотезу о том, что все групповые средства равны, и делает вывод, что по меньшей мере одно из групповых средств отличается от других. Наиболее распространенные уровни значимости составляют 0,05 и 0,01.

Таблица ANOVA

Таблица ANOVA фиксирует изменчивость в модели по источникам, F-статистику для проверки значимости этой изменчивости и p-значение для принятия решения о значимости этой изменчивости. Значение p, возвращаемое anova1 зависит от предположений о случайных возмущениях в уравнении модели. Чтобы значение p было правильным, эти возмущения должны быть независимыми, нормально распределенными и иметь постоянную дисперсию. Стандартная таблица ANOVA имеет следующий вид:

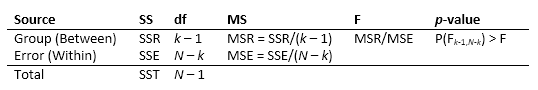
anova1 возвращает стандартную таблицу ANOVA в виде массива ячеек с шестью столбцами.

Колонка	Определение
`Source`	Источник изменчивости.
`SS`	Сумма квадратов для каждого источника.
`df`	Степени свободы, связанные с каждым источником. Предположим, что N - общее число наблюдений, а k - число групп. Затем N - k - внутригрупповые степени свободы (`Error`), k - 1 - межгрупповые степени свободы (`Columns`), а N - 1 - суммарные степени свободы: N - 1 = (N - k) + (k - 1).
`MS`	Средние квадраты для каждого источника, которое является отношением `SS/df`.
`F`	F-статистика, которая является отношением средних квадратов.
`Prob>F`	p-значение, которое является вероятностью того, что F-статистика может принять значение, большее, чем вычисленное значение test-statistic. `anova1` извлекает эту вероятность из cdF-распределения.

Строки таблицы ANOVA показывают изменчивость данных, деленную на источник.

Строка (источник)	Определение
`Groups` или `Columns`	Изменчивость из-за различий между групповыми средами (изменчивость между группами)
`Error`	Изменчивость из-за различий между данными в каждой группе и средним значением группы (изменчивость в группах)
`Total`	Общая изменчивость

Ссылки

[1] Wu, C. F. J. и M. Hamada. Эксперименты: планирование, анализ и оптимизация проектирования параметров, 2000.

[2] Нетер, Дж., М. Х. Кутнер, С. Дж. Нахтсхайм и В. Вассерман. 4-е ред. Прикладные линейные статистические модели. Ирвин Пресс, 1996.

См. также

anova1 | kruskalwallis | multcompare

Документация