График 3-D неявное уравнение или функция
fimplicit3( готовит 3D неявное уравнение или функцию f)f(x,y,z) за интервал по умолчанию [-5 5] для x, y, и z.
fimplicit3( сюжеты f,[xmin xmax ymin ymax zmin zmax])f(x,y,z) за интервал [xmin xmax] для x, [ymin ymax] для y, и [zmin zmax] для z. fimplicit3 функции использует symvar упорядочить переменные и назначить интервалы.
fimplicit3(___, использование LineSpec)LineSpec для задания стиля линии, обозначения маркера и цвета грани.
fimplicit3(___, задание свойств линий с использованием одного или нескольких Name,Value)Name,Value аргументы пары. Используйте эту опцию с любой из комбинаций входных аргументов в предыдущих синтаксисах.
fimplicit3( строит графики в осях с объектом ax,___)ax вместо текущего объекта-оси gca.
fi = fimplicit3(___)
Постройте график гиперболоида = 0 с помощью fimplicit3. fimplicit3 график функции в интервале по умолчанию для , и .
syms x y z fimplicit3(x^2 + y^2 - z^2)

Постройте график гиперболоида, заданного функцией + y2-z2. fimplicit3 график функции в интервале по умолчанию [для xy и z
syms f(x,y,z)
f(x,y,z) = x^2 + y^2 - z^2;
fimplicit3(f)
Задайте интервал печати, указав второй аргумент для fimplicit3. Постройте график верхней половины гиперболоида = 0, указав < z < 5. значений x и y используйте интервал по умолчанию [-5,5].
syms x y z f = x^2 + y^2 - z^2; interval = [-5 5 -5 5 0 5]; fimplicit3(f, interval)

Постройте график неявного уравнения x) = 0 на 2δ, 2λ) для всех осей.
Создайте засечки оси X, охватывая пределы оси X с интервалами, равными pi/2. Преобразование пределов оси в точные кратные pi/2 с помощью round и получить символьные значения делений в S. Отображение этих засечек с помощью XTick собственность. Создание меток оси X с помощью arrayfun подавать texlabel кому S. Отображение этих меток с помощью XTickLabel собственность. Повторите эти шаги для оси Y.
Сведения об использовании LaTeX на графиках см. в разделе latex.
syms x y z eqn = x*sin(y) + z*cos(x); fimplicit3(eqn,[-2*pi 2*pi]) title('xsin(y) + zcos(x) for -2\pi < x < 2\pi and -2\pi < y < 2\pi') xlabel('x') ylabel('y') ax = gca; S = sym(ax.XLim(1):pi/2:ax.XLim(2)); S = sym(round(vpa(S/pi*2))*pi/2); ax.XTick = double(S); ax.XTickLabel = arrayfun(@texlabel,S,'UniformOutput',false); S = sym(ax.YLim(1):pi/2:ax.YLim(2)); S = sym(round(vpa(S/pi*2))*pi/2); ax.YTick = double(S); ax.YTickLabel = arrayfun(@texlabel, S, 'UniformOutput', false);

Постройте график неявной поверхности = 0 с различными стилями линий для различных значений z. < z < -2 используйте пунктирную линию с зелеными Для -2 < z < 2 используйтеLineWidth из 1 и зеленый цвет лица. Для < 5 отключите линии установкой EdgeColor кому none.
syms x y z f = x^2 + y^2 - z^2; fimplicit3(f,[-5 5 -5 5 -5 -2],'--.','MarkerEdgeColor','g') hold on fimplicit3(f,[-5 5 -5 5 -2 2],'LineWidth',1,'FaceColor','g') fimplicit3(f,[-5 5 -5 5 2 5],'EdgeColor','none')

Постройте график неявной поверхности = 0. Укажите вывод для выводаfimplicit3 вернуть объект печати.
syms x y z f = 1/x^2 - 1/y^2 + 1/z^2; fi = fimplicit3(f)

fi =
ImplicitFunctionSurface with properties:
Function: [1x1 sym]
EdgeColor: [0 0 0]
LineStyle: '-'
FaceColor: 'interp'
Show all properties
Показать только положительную ось X, задав значение XRange имущество fi кому [0 5]. Удалите линии, установив EdgeColor свойство для 'none'. Визуализировать скрытые поверхности, сделав график прозрачным, установив FaceAlpha свойство для 0.8.
fi.XRange = [0 5];
fi.EdgeColor = 'none';
fi.FaceAlpha = 0.8;
Управление разрешением неявного графика поверхности с помощью 'MeshDensity' вариант. Увеличение 'MeshDensity' может сделать более плавные, более точные графики при уменьшении 'MeshDensity' может увеличить скорость печати.
Разделить фигуру на две с помощью subplot. В первом вложенном графике постройте график неявного поверхностного )). Поверхность имеет большие зазоры. Устраните эту проблему, увеличив 'MeshDensity' кому 40 на втором вложенном графике. fimplicit3 заполняет пробелы, показывая, что путем увеличения 'MeshDensity' увеличена разрешающая способность графика.
syms x y z f = sin(1/(x*y*z)); subplot(2,1,1) fimplicit3(f) title('Default MeshDensity = 35') subplot(2,1,2) fimplicit3(f,'MeshDensity',40) title('Increased MeshDensity = 40')

Применение поворота и перемещения к неявному графику поверхности тора.
Тор может быть определен неявным уравнением в декартовых координатах как
2-4R2 (x2 + y2)
где
- радиус трубки;
- расстояние от центра трубы до центра тора;
Определите значения для и как 1 и 5 соответственно. Постройте график тора с помощью fimplicit3.
syms x y z a = 1; R = 4; f(x,y,z) = (x^2+y^2+z^2+R^2-a^2)^2 - 4*R^2*(x^2+y^2); fimplicit3(f) hold on
Примените поворот к тору вокруг оси X. Определите матрицу поворота. Поверните тор на 90 градусов или радиана. Сместите центр тора на 5 вдоль оси X.
alpha = pi/2;
Rx = [1 0 0;
0 cos(alpha) sin(alpha);
0 -sin(alpha) cos(alpha)];
r = [x; y; z];
r_90 = Rx*r;
g = subs(f,[x,y,z],[r_90(1)-5,r_90(2),r_90(3)]);Добавьте второй график повернутого и перемещенного тора к существующему графу.
fimplicit3(g)
axis([-5 10 -5 10 -5 5])
hold off
f - 3-D неявное уравнение или функцию для построения графика3-D неявное уравнение или функцию для построения графика, заданную как символическое уравнение, выражение или функция. Если указано выражение или функция, то fimplicit3 предполагает, что правый размер должен быть 0.
[min max] - Интервал печати для осей x, y и z-Интервал печати для осей x, y и z, заданный как вектор из двух чисел. Значение по умолчанию: [-5 5].
[xmin xmax ymin ymax zmin zmax] - Интервал печати для осей x, y и z-Интервал печати для осей x, y и z, заданный как вектор из шести чисел. Значение по умолчанию: [-5 5 -5 5 -5 5].
ax - Объект AxesОбъект Axes. Если объект axes не указан, то fimplicit3 использует текущие оси.
LineSpec - Стиль линии, маркер и цветСтиль линии, маркер и цвет, заданные как символьный вектор или строка, содержащая символы. Символы могут отображаться в любом порядке. Нет необходимости указывать все три признака (стиль линии, маркер и цвет). Например, если опустить стиль линии и указать маркер, на графике будет отображаться только маркер и ни одной линии.
Пример: '--or' - красная пунктирная линия с маркерами окружности
| Стиль линии | Описание |
|---|---|
- | Сплошная линия |
-- | Пунктирная линия |
: | Пунктирная линия |
-. | Черточно-точечная линия |
| Маркер | Описание |
|---|---|
'o' | Круг |
'+' | Знак «Плюс» |
'*' | Звездочка |
'.' | Пункт |
'x' | Крест |
'_' | Горизонтальная линия |
'|' | Вертикальная линия |
's' | Квадрат |
'd' | Алмаз |
'^' | Треугольник, направленный вверх |
'v' | Треугольник, направленный вниз |
'>' | Прямоугольный треугольник |
'<' | Треугольник, указывающий влево |
'p' | Пентаграмма |
'h' | Hexagram |
| Цвет | Описание |
|---|---|
| желтый |
| пурпурный |
| голубой |
| красный |
| зеленый |
| синий |
| белый |
| черный |
Укажите дополнительные пары, разделенные запятыми Name,Value аргументы. Name является именем аргумента и Value - соответствующее значение. Name должен отображаться внутри кавычек. Можно указать несколько аргументов пары имен и значений в любом порядке как Name1,Value1,...,NameN,ValueN.
'Marker','o','MarkerFaceColor','red'Перечисленные здесь свойства являются только подмножеством. Полный список см. в разделе Свойства ImplicitFuncterSurface.
'MeshDensity' - Количество точек оценки на направлениеКоличество точек оценки на направление, указанное как число. Значение по умолчанию: 35.
Пример: 100
'EdgeColor' - Цвет линии[0 0 0] (по умолчанию) | 'interp' | Триплет RGB | шестнадцатеричный цветовой код | 'r' | 'g' | 'b' | ...Цвет линии, указан как 'interp', триплет RGB, шестнадцатеричный цветовой код, имя цвета или короткое имя. Значение триплета RGB по умолчанию [0 0 0] соответствует черному. 'interp' значение цветит края на основе ZData значения.
Для пользовательского цвета укажите триплет RGB или шестнадцатеричный цветовой код.
Триплет RGB - это трехэлементный вектор строки, элементы которого задают интенсивности красной, зеленой и синей составляющих цвета. Интенсивности должны находиться в диапазоне [0,1]; например, [0.4 0.6 0.7].
Шестнадцатеричный цветовой код - это символьный вектор или строковый скаляр, начинающийся с хэш-символа (#), за которыми следуют три или шесть шестнадцатеричных цифр, которые могут варьироваться от 0 кому F. Значения не чувствительны к регистру. Таким образом, цветовые коды '#FF8800', '#ff8800', '#F80', и '#f80' эквивалентны.
Можно также задать некоторые общие цвета по имени. В этой таблице перечислены параметры именованного цвета, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.
| Имя цвета | Краткое имя | Триплет RGB | Шестнадцатеричный цветовой код | Внешность |
|---|---|---|---|---|
'red' | 'r' | [1 0 0] | '#FF0000' |
|
'green' | 'g' | [0 1 0] | '#00FF00' |
|
'blue' | 'b' | [0 0 1] | '#0000FF' |
|
'cyan'
| 'c' | [0 1 1] | '#00FFFF' |
|
'magenta' | 'm' | [1 0 1] | '#FF00FF' |
|
'yellow' | 'y' | [1 1 0] | '#FFFF00' |
|
'black' | 'k' | [0 0 0] | '#000000' |
|
'white' | 'w' | [1 1 1] | '#FFFFFF' |
|
'none' | Неприменимо | Неприменимо | Неприменимо | Без цвета |
Вот триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию MATLAB ®, используемых на многих типах графиков.
| Триплет RGB | Шестнадцатеричный цветовой код | Внешность |
|---|---|---|
[0 0.4470 0.7410] | '#0072BD' |
|
[0.8500 0.3250 0.0980] | '#D95319' |
|
[0.9290 0.6940 0.1250] | '#EDB120' |
|
[0.4940 0.1840 0.5560] | '#7E2F8E' |
|
[0.4660 0.6740 0.1880] | '#77AC30' |
|
[0.3010 0.7450 0.9330] | '#4DBEEE' |
|
[0.6350 0.0780 0.1840] | '#A2142F' |
|
'LineStyle' - Стиль линии'-' (по умолчанию) | '--' | ':' | '-.' | 'none'Стиль линии, указанный в качестве одного из параметров, перечисленных в этой таблице.
| Стиль линии | Описание | Результирующая линия |
|---|---|---|
'-' | Сплошная линия |
|
'--' | Пунктирная линия |
|
':' | Пунктирная линия |
|
'-.' | Пунктирная линия |
|
'none' | Без строки | Без строки |
'LineWidth' - Ширина линии0.5 (по умолчанию) | положительное значениеШирина линии, заданная как положительное значение в точках, где 1 точка = 1/72 дюйма. Если линия имеет маркеры, то ширина линии также влияет на кромки маркера.
Ширина линии не может быть меньше ширины пикселя. Если задать для ширины линии значение, меньшее, чем ширина пикселя в системе, линия будет отображаться в виде одного пикселя в ширину.
'Marker' - Символ маркера'none' (по умолчанию) | 'o' | '+' | '*' | '.' | ...Символ маркера, указанный как одно из значений, перечисленных в этой таблице. По умолчанию объект не отображает маркеры. Задание обозначения маркера добавляет маркеры в каждую точку данных или вершину.
| Стоимость | Описание |
|---|---|
'o' | Круг |
'+' | Знак «Плюс» |
'*' | Звездочка |
'.' | Пункт |
'x' | Крест |
'_' | Горизонтальная линия |
'|' | Вертикальная линия |
'square' или 's' | Квадрат |
'diamond' или 'd' | Алмаз |
'^' | Треугольник, направленный вверх |
'v' | Треугольник, направленный вниз |
'>' | Прямоугольный треугольник |
'<' | Треугольник, указывающий влево |
'pentagram' или 'p' | Пятиконечная звезда (пентаграмма) |
'hexagram' или 'h' | Шестиконечная звезда (гексаграмма) |
'none' | Без маркеров |
'MarkerEdgeColor' - Цвет контура маркера'auto' (по умолчанию) | триплет RGB | шестнадцатеричный цветовой код | 'r' | 'g' | 'b' | ...Цвет контура маркера, указанный как 'auto', триплет RGB, шестнадцатеричный цветовой код, имя цвета или короткое имя. Значение по умолчанию 'auto' использует тот же цвет, что и EdgeColor собственность.
Для пользовательского цвета укажите триплет RGB или шестнадцатеричный цветовой код.
Триплет RGB - это трехэлементный вектор строки, элементы которого задают интенсивности красной, зеленой и синей составляющих цвета. Интенсивности должны находиться в диапазоне [0,1]; например, [0.4 0.6 0.7].
Шестнадцатеричный цветовой код - это символьный вектор или строковый скаляр, начинающийся с хэш-символа (#), за которыми следуют три или шесть шестнадцатеричных цифр, которые могут варьироваться от 0 кому F. Значения не чувствительны к регистру. Таким образом, цветовые коды '#FF8800', '#ff8800', '#F80', и '#f80' эквивалентны.
Можно также задать некоторые общие цвета по имени. В этой таблице перечислены параметры именованного цвета, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.
| Имя цвета | Краткое имя | Триплет RGB | Шестнадцатеричный цветовой код | Внешность |
|---|---|---|---|---|
'red' | 'r' | [1 0 0] | '#FF0000' |
|
'green' | 'g' | [0 1 0] | '#00FF00' |
|
'blue' | 'b' | [0 0 1] | '#0000FF' |
|
'cyan'
| 'c' | [0 1 1] | '#00FFFF' |
|
'magenta' | 'm' | [1 0 1] | '#FF00FF' |
|
'yellow' | 'y' | [1 1 0] | '#FFFF00' |
|
'black' | 'k' | [0 0 0] | '#000000' |
|
'white' | 'w' | [1 1 1] | '#FFFFFF' |
|
'none' | Неприменимо | Неприменимо | Неприменимо | Без цвета |
Вот триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию MATLAB, используемых на многих типах графиков.
| Триплет RGB | Шестнадцатеричный цветовой код | Внешность |
|---|---|---|
[0 0.4470 0.7410] | '#0072BD' |
|
[0.8500 0.3250 0.0980] | '#D95319' |
|
[0.9290 0.6940 0.1250] | '#EDB120' |
|
[0.4940 0.1840 0.5560] | '#7E2F8E' |
|
[0.4660 0.6740 0.1880] | '#77AC30' |
|
[0.3010 0.7450 0.9330] | '#4DBEEE' |
|
[0.6350 0.0780 0.1840] | '#A2142F' |
|
Пример: [0.5 0.5 0.5]
Пример: 'blue'
Пример: '#D2F9A7'
'MarkerFaceColor' - Цвет заливки маркера'none' (по умолчанию) | 'auto' | Триплет RGB | шестнадцатеричный цветовой код | 'r' | 'g' | 'b' | ...Цвет заливки маркера, указанный как 'auto', триплет RGB, шестнадцатеричный цветовой код, имя цвета или короткое имя. 'auto' значение использует тот же цвет, что и MarkerEdgeColor собственность.
Для пользовательского цвета укажите триплет RGB или шестнадцатеричный цветовой код.
Триплет RGB - это трехэлементный вектор строки, элементы которого задают интенсивности красной, зеленой и синей составляющих цвета. Интенсивности должны находиться в диапазоне [0,1]; например, [0.4 0.6 0.7].
Шестнадцатеричный цветовой код - это символьный вектор или строковый скаляр, начинающийся с хэш-символа (#), за которыми следуют три или шесть шестнадцатеричных цифр, которые могут варьироваться от 0 кому F. Значения не чувствительны к регистру. Таким образом, цветовые коды '#FF8800', '#ff8800', '#F80', и '#f80' эквивалентны.
Можно также задать некоторые общие цвета по имени. В этой таблице перечислены параметры именованного цвета, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.
| Имя цвета | Краткое имя | Триплет RGB | Шестнадцатеричный цветовой код | Внешность |
|---|---|---|---|---|
'red' | 'r' | [1 0 0] | '#FF0000' |
|
'green' | 'g' | [0 1 0] | '#00FF00' |
|
'blue' | 'b' | [0 0 1] | '#0000FF' |
|
'cyan'
| 'c' | [0 1 1] | '#00FFFF' |
|
'magenta' | 'm' | [1 0 1] | '#FF00FF' |
|
'yellow' | 'y' | [1 1 0] | '#FFFF00' |
|
'black' | 'k' | [0 0 0] | '#000000' |
|
'white' | 'w' | [1 1 1] | '#FFFFFF' |
|
'none' | Неприменимо | Неприменимо | Неприменимо | Без цвета |
Вот триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию MATLAB, используемых на многих типах графиков.
| Триплет RGB | Шестнадцатеричный цветовой код | Внешность |
|---|---|---|
[0 0.4470 0.7410] | '#0072BD' |
|
[0.8500 0.3250 0.0980] | '#D95319' |
|
[0.9290 0.6940 0.1250] | '#EDB120' |
|
[0.4940 0.1840 0.5560] | '#7E2F8E' |
|
[0.4660 0.6740 0.1880] | '#77AC30' |
|
[0.3010 0.7450 0.9330] | '#4DBEEE' |
|
[0.6350 0.0780 0.1840] | '#A2142F' |
|
Пример: [0.3 0.2 0.1]
Пример: 'green'
Пример: '#D2F9A7'
'MarkerSize' - Размер маркера6 (по умолчанию) | положительное значениеРазмер маркера, заданный как положительное значение в точках, где 1 точка = 1/72 дюйма.
fi - Один или несколько объектовОдин или несколько объектов, возвращаемых как скаляр или вектор. Объект является неявным объектом поверхности функции. Эти объекты можно использовать для запроса и изменения свойств определенной строки. Дополнительные сведения см. в разделе Свойства ImplicitFuncterSurface.
fimplicit3 назначает символьные переменные в f в x ось, y ось, затем z ось, и symvar определяет порядок присваиваемых переменных. Поэтому имена переменных и осей могут не соответствовать друг другу. Вызвать fimplicit3 чтобы назначить x, y или z соответствующей оси, создайте символическую функцию для печати, а затем передайте символическую функцию в fimplicit3.
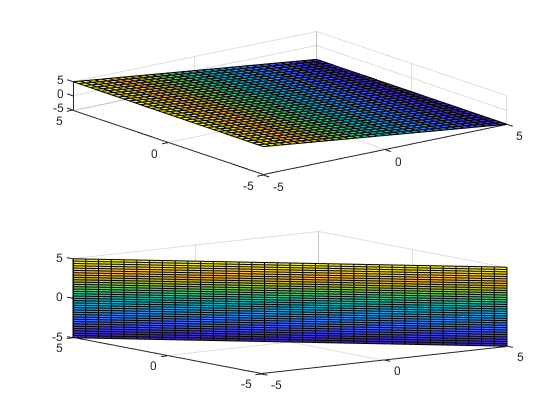
Например, следующий код отображает корни неявной функции f (x, y, z) = x + z двумя способами. Первый путь силfimplicit3 для назначения осей x и z соответствующим осям. Во-вторых, fimplicit3 откладывает до symvar для определения назначения переменного порядка и оси: fimplicit3 присваивает оси x и y соответственно.
syms x y z; f(x,y,z) = x + z; figure; subplot(2,1,1) fimplicit3(f); view(-38,71); subplot(2,1,2) fimplicit3(f(x,y,z)); % Or fimplicit3(x + z);
Имеется измененная версия этого примера. Открыть этот пример с помощью изменений?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.