Печать нескольких линий на одной фигуре

Можно распечатать несколько линий, передав входные данные в виде вектора или используя hold on для последовательного построения графика на одной и той же фигуре. При указании LineSpec и аргументы Name-Value, они применяются ко всем строкам. Чтобы задать опции для отдельных графиков, используйте дескрипторы функций, возвращаемые fplot.

Разделить фигуру на два вложенных графика с помощью subplot. На первом вложенном графике постройте график $$\sin (x$$) и $$\mathrm{}cos($$x) с использованием векторного ввода. На втором вложенном графике $$\mathrm{постройте\; график}\sin$$(x) $$\mathrm{и}cos$$ (x) с использованиемhold on.

syms x
subplot(2,1,1)
fplot([sin(x) cos(x)])
title('Multiple Lines Using Vector Inputs')

subplot(2,1,2)
fplot(sin(x))
hold on
fplot(cos(x))
title('Multiple Lines Using hold on Command')

hold off

Изменение свойств линий и отображаемых маркеров

Постройте график трех синусоидальных кривых с фазовым сдвигом между каждой линией. Для первой строки используйте ширину линии 2. Во-вторых, задайте стиль красной пунктирной линии с маркерами окружности. В третьем случае задайте голубой, тире-точечный стиль линии с маркерами звездочки. Отображение легенды.

syms x
fplot(sin(x+pi/5),'Linewidth',2)
hold on
fplot(sin(x-pi/5),'--or')
fplot(sin(x),'-.*c')
legend('show','Location','best')
hold off

Контрольное разрешение графика

Управление разрешением графика с помощью MeshDensity вариант. Увеличение MeshDensity позволяет сделать более плавные и точные графики, уменьшая при этом скорость печати.

Разделить фигуру на две с помощью subplot. В первом вложенном графике постройте график ступенчатой функции из x = 2.1 кому x = 2.15. Разрешение графика слишком низкое для обнаружения функции шага. Устраните эту проблему, увеличив MeshDensity кому 39 на втором вложенном графике. Теперь график обнаруживает функцию шага и показывает, что путем увеличения MeshDensity вы увеличили разрешение графика.

syms x
stepFn = rectangularPulse(2.1, 2.15, x);

subplot(2,1,1)
fplot(stepFn);
title('Default MeshDensity = 23')

subplot(2,1,2)
fplot(stepFn,'MeshDensity',39);
title('Increased MeshDensity = 39')

Изменение графика после создания

График sin(x). Укажите вывод для вывода fplot вернуть объект печати.

syms x
h = fplot(sin(x))

h = 
  FunctionLine with properties:

     Function: [1x1 sym]
        Color: [0 0.4470 0.7410]
    LineStyle: '-'
    LineWidth: 0.5000

  Show all properties

Измените синюю линию по умолчанию на пунктирную красную линию, используя точечное представление для задания свойств. Аналогично, добавить 'x' маркеры и установите синий цвет маркера.

h.LineStyle = '--';
h.Color = 'r';
h.Marker = 'x';
h.MarkerEdgeColor = 'b';

Добавление меток заголовка и оси и засечек формата

Для $$x$$ от $$-\mathrm{}\mathrm{2\lambda }$$ до $$\mathrm{}\mathrm{2\lambda }$$, постройте график $$\sin (x$$). Добавьте заголовок и метки оси. Создайте засечки оси X, охватывая пределы оси X с интервалами, равнымиpi/2. Отображение этих засечек с помощью XTick собственность. Создание меток оси X с помощью arrayfun подавать texlabel кому S. Отображение этих меток с помощью XTickLabel собственность.

Сведения об использовании LaTeX на графиках см. в разделе latex.

syms x
fplot(sin(x),[-2*pi 2*pi])
grid on
title('sin(x) from -2\pi to 2\pi')
xlabel('x')
ylabel('y')

ax = gca;
S = sym(ax.XLim(1):pi/2:ax.XLim(2));
ax.XTick = double(S);
ax.XTickLabel = arrayfun(@texlabel,S,'UniformOutput',false);

Повторная оценка при масштабировании

При увеличении масштаба графика fplot автоматически пересчитывает график. Эта повторная оценка масштаба показывает скрытые детали при меньших масштабах.

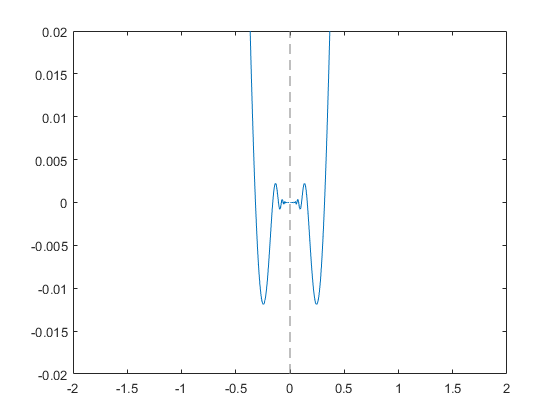
График x^3*sin(1/x) для -2 < x < 2 и -0.02 < y < 0.02. Увеличение масштаба графика с помощью zoom и перерисовать график с помощью drawnow. Из-за повторной оценки при увеличении, fplot раскрывает детали меньшего масштаба. Повторите зумирование 6 раз, чтобы просмотреть сведения меньшего масштаба. Чтобы воспроизвести анимацию, щелкните изображение.

syms x
fplot(x^3*sin(1/x));
axis([-2 2 -0.02 0.02]);
for i=1:6
    zoom(1.7)
    pause(0.5)
end

Создание анимаций

Создание анимации путем изменения отображаемого выражения с помощью Function, XFunction, и YFunction свойства и затем с помощью drawnow для обновления графика. Сведения об экспорте в GIF см. в разделе imwrite.

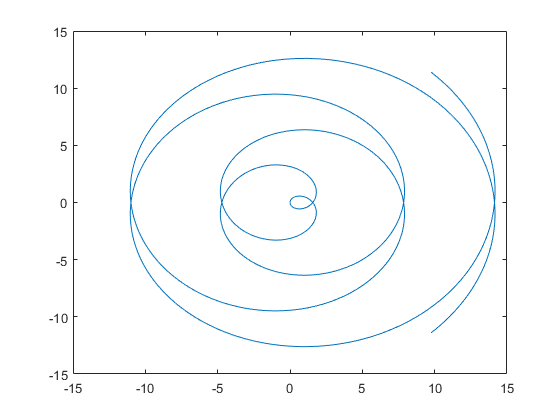
Изменяя переменную i от 0,1 до 3, анимируйте параметрическую кривую

Чтобы воспроизвести анимацию, щелкните изображение.

syms t
fp = fplot(t, t);
axis([-15 15 -15 15])
for i=0.1:0.05:3
    fp.XFunction = i.*t.*sin(i*t);
    fp.YFunction = i.*t.*cos(i*t);
    drawnow
end