fsurf

Печать поверхности 3-D

свернуть все на странице

Синтаксис

fsurf (f)

fsurf (f, [min max])

fsurf (f, [xmin xmax ymin ymax])

fsurf (funx, funy, funz)

fsurf (funx, funy, funz, [uvmin uvmax])

fsurf (funx, funy, funz, [umin umax vmin vmax])

fsurf (___, LineSpec)

fsurf (___, имя, значение)

fsurf (топор, ___)

fs = fsurf (___)

Описание

пример

fsurf(f) создает график поверхности символьного выражения f(x,y) за интервал по умолчанию [-5 5] для x и y.

пример

fsurf(f,[min max]) сюжеты f(x,y) за интервал [min max] для x и y.

пример

fsurf(f,[xmin xmax ymin ymax]) сюжеты f(x,y) за интервал [xmin xmax] для x и [ymin ymax] для y. fsurf функции использует symvar упорядочить переменные и назначить интервалы.

пример

fsurf(funx,funy,funz) отображает параметрическую поверхность x = x(u,v), y = y(u,v), z = z(u,v) за интервал [-5 5] для u и v.

fsurf(funx,funy,funz,[uvmin uvmax]) отображает параметрическую поверхность x = x(u,v), y = y(u,v), z = z(u,v) за интервал [uvmin uvmax] для u и v.

пример

fsurf(funx,funy,funz,[umin umax vmin vmax]) отображает параметрическую поверхность x = x(u,v), y = y(u,v), z = z(u,v) за интервал [umin umax] для u и [vmin vmax] для v. fsurf функции использует symvar упорядочить параметрические переменные и назначить интервалы.

пример

fsurf(___,LineSpec) использование LineSpec для задания стиля линии, обозначения маркера и цвета грани. Используйте эту опцию после любой из предыдущих комбинаций входных аргументов.

пример

fsurf(___,Name,Value) задание свойств линий с использованием одного или нескольких Name,Value аргументы пары. Используйте эту опцию после любой комбинации входных аргументов в предыдущих синтаксисах.

fsurf(ax,___) строит графики в осях с объектом ax вместо текущего объекта-оси gca.

пример

fs = fsurf(___) возвращает объект поверхности функции или параметризованный объект поверхности функции в зависимости от типа поверхности. Объект используется для запроса и изменения свойств определенной поверхности. Дополнительные сведения см. в разделах Функции Свойства поверхности и Параметры Функции Свойства поверхности.

Примеры

3-D График поверхности символьного выражения

Постройте график входного $\sin (x) + cos$ (y) в $диапазоне$ по умолчанию -5 < x $< 5$ и -5 < y < 5.

syms x y
fsurf(sin(x)+cos(y))

Figure contains an axes. The axes contains an object of type functionsurface.

3-D График поверхности символьной функции

Постройте график действительной части $^{tan-1} (x +$ iy) в $диапазоне$ по умолчанию -5 < x < $5 и$ -5 < y < 5.

syms f(x,y)
f(x,y) = real(atan(x + i*y));
fsurf(f)

Figure contains an axes. The axes contains an object of type functionsurface.

Задание интервала печати поверхности

Постройте график $\sin (x) + cos$ (y) $над - λ$ < x $< λ$ и -5 < y < 5, указав интервал печати в качестве второго аргументаfsurf.

syms x y
f = sin(x) + cos(y);
fsurf(f, [-pi pi -5 5])

Figure contains an axes. The axes contains an object of type functionsurface.

Параметризованный график поверхности

Печать параметризованной поверхности

$\begin{array}{c} x = rcos (s) \\ \sin (t) y = rsin \\ (s) sin ( \\ t) z = rcos (t) \end{array}$ где = 2 + sin (7s + 5t)

для $0 < s$ < 2δ $и 0$ < t < δ.

Улучшение внешнего вида графика с помощью camlight.

syms s t
r = 2 + sin(7*s + 5*t);
x = r*cos(s)*sin(t);
y = r*sin(s)*sin(t);
z = r*cos(t);
fsurf(x, y, z, [0 2*pi 0 pi])
camlight
view(46,52)

Figure contains an axes. The axes contains an object of type parameterizedfunctionsurface.

График поверхности кусочного выражения

Постройте график кусочного выражения бутылки Кляйна

$\begin{array}{l} x (u, v) \begin{matrix} = {-4, потому что (u) [1+sin (u)] -r (u), потому что (u) & , потому что \\ (v) 0 <u ≤π -4, потому что (u) [1+sin (u)] & +r (u) \end{matrix} \\ , потому что (v) π < u < 2π год ( \\ u, v) =r \begin{matrix} (u) грех (v) z (u, v) = {-14 грехов & (u) \\ -r (u) грех & (u), потому что \end{matrix} \\ (v) 0 < u \leqπ -14 грехов \end{array}$ (u) π <u <2π, где r (u) =4-2, потому что (u)

для $0 < u$ < 2δ $и 0$ < v < 2δ.

Покажите, что бутылка Кляйна имеет только одностороннюю поверхность.

syms u v;
r = @(u) 4 - 2*cos(u);
x = piecewise(u <= pi, -4*cos(u)*(1+sin(u)) - r(u)*cos(u)*cos(v),...
    u > pi, -4*cos(u)*(1+sin(u)) + r(u)*cos(v));
y = r(u)*sin(v);
z = piecewise(u <= pi, -14*sin(u) - r(u)*sin(u)*cos(v),...
    u > pi, -14*sin(u));
h = fsurf(x,y,z, [0 2*pi 0 2*pi]);

Figure contains an axes. The axes contains an object of type parameterizedfunctionsurface.

Добавление меток заголовка и оси и засечек формата

Для $x$ и $y$ от $- 2λ$ до $2λ$ постройте график 3-D поверхности $ysin (x) - xcos$ (y). Добавьте заголовок и метки оси.

Создайте засечки оси X, охватывая пределы оси X с интервалами, равными pi/2. Преобразование пределов оси в точные кратные pi/2 с помощью round и получить символьные значения делений в S. Отображение этих засечек с помощью XTick собственность. Создание меток оси X с помощью arrayfun подавать texlabel кому S. Отображение этих меток с помощью XTickLabel собственность. Повторите эти шаги для оси Y.

Сведения об использовании LaTeX на графиках см. в разделе latex.

syms x y
fsurf(y.*sin(x)-x.*cos(y), [-2*pi 2*pi])
title('ysin(x) - xcos(y) for x and y in [-2\pi,2\pi]')
xlabel('x')
ylabel('y')
zlabel('z')

ax = gca;
S = sym(ax.XLim(1):pi/2:ax.XLim(2));
S = sym(round(vpa(S/pi*2))*pi/2);
ax.XTick = double(S);
ax.XTickLabel = arrayfun(@texlabel,S,'UniformOutput',false);

S = sym(ax.YLim(1):pi/2:ax.YLim(2));
S = sym(round(vpa(S/pi*2))*pi/2);
ax.YTick = double(S);
ax.YTickLabel = arrayfun(@texlabel,S,'UniformOutput',false);

$Figure contains an axes. The axes with title ysin(x) - xcos(y) for x and y in [-2\pi,2\pi] contains an object of type functionsurface.$

Стиль и ширина линий для печати поверхности

Постройте график параметрической поверхности $x = ssin$ (t $), y = -$ scos $(t$ ), z = t с различными стилями линий для различных значений $t. Для$ -5 < t < -2 используйте пунктирную линию с зелеными $точечными маркерами$ . Для - 2 < t < 2 используйтеLineWidth из 1 и зеленый цвет лица. Для $2 < t$ < 5 отключите линии установкой EdgeColor кому none.

syms s t
fsurf(s*sin(t),-s*cos(t),t,[-5 5 -5 -2],'--.','MarkerEdgeColor','g')
hold on
fsurf(s*sin(t),-s*cos(t),t,[-5 5 -2 2],'LineWidth',1,'FaceColor','g')
fsurf(s*sin(t),-s*cos(t),t,[-5 5 2 5],'EdgeColor','none')

Figure contains an axes. The axes contains 3 objects of type parameterizedfunctionsurface.

Изменить поверхность после создания

Печать параметрической поверхности

$\begin{array}{c} x =^{e - | u} |/10sin \\ (5^{| v |)} y = e - | \\ u \end{array}$ |/10cos (5 | v |) z = u.

Укажите вывод для вывода fcontour вернуть объект печати.

syms u v
x = exp(-abs(u)/10).*sin(5*abs(v));
y = exp(-abs(u)/10).*cos(5*abs(v));
z = u;
fs = fsurf(x,y,z)

Figure contains an axes. The axes contains an object of type parameterizedfunctionsurface.

fs = 
  ParameterizedFunctionSurface with properties:

    XFunction: [1x1 sym]
    YFunction: [1x1 sym]
    ZFunction: [1x1 sym]
    EdgeColor: [0 0 0]
    LineStyle: '-'
    FaceColor: 'interp'

  Show all properties

Изменение диапазона u кому [-30 30] с помощью URange имущество fs. Установите синий цвет линии с помощью кнопки EdgeColor и укажите белые точечные маркеры с помощью Marker и MarkerEdgeColor свойства.

fs.URange = [-30 30];
fs.EdgeColor = 'b';
fs.Marker = '.';
fs.MarkerEdgeColor = 'w';

Figure contains an axes. The axes contains an object of type parameterizedfunctionsurface.

Графики нескольких поверхностей и прозрачные поверхности

Печать нескольких поверхностей с использованием векторного ввода в fsurf. В качестве альтернативы можно использовать hold on для последовательного построения графика на одной и той же фигуре. При отображении нескольких поверхностей на одной фигуре используется прозрачность. Скорректируйте прозрачность графиков поверхности с помощью команды FaceAlpha собственность. FaceAlpha варьируется от 0 кому 1, где 0 является полной прозрачностью и 1 отсутствует прозрачность.

Постройте график плоскостей $x +$ y $и$ x-y с помощью векторного ввода вfsurf. Показать обе плоскости, сделав их наполовину прозрачными с помощью FaceAlpha.

syms x y
h = fsurf([x+y x-y]);
h(1).FaceAlpha = 0.5;
h(2).FaceAlpha = 0.5;
title('Planes (x+y) and (x-y) at half transparency')

Figure contains an axes. The axes with title Planes (x+y) and (x-y) at half transparency contains 2 objects of type functionsurface.

Управляющее разрешение поверхностного графика

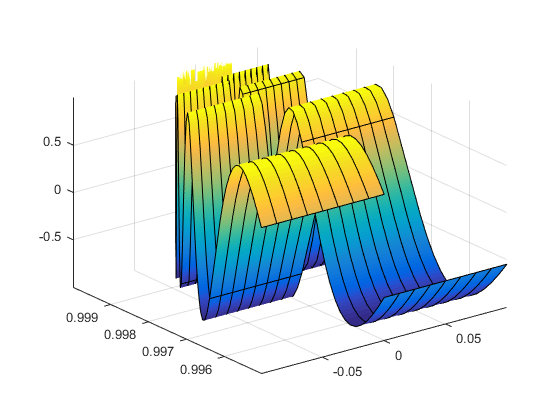
Управление разрешением графика поверхности с помощью команды 'MeshDensity' вариант. Увеличение 'MeshDensity' позволяет сделать более плавные и точные графики, уменьшая при этом скорость печати.

Разделить фигуру на две с помощью subplot. В первом вложенном графике постройте график параметрической поверхности $x = \sin$ (s $), y =$ cos (s) $и z = (t/10)$ sin (1/s). Поверхность имеет большой зазор. Устраните эту проблему, увеличив'MeshDensity' кому 40 на втором вложенном графике. fsurf заполняет пробел, показывая, что, увеличивая 'MeshDensity' вы увеличили разрешение графика.

syms s t

subplot(2,1,1)
fsurf(sin(s), cos(s), t/10.*sin(1./s))
view(-172,25)
title('Default MeshDensity = 35')

subplot(2,1,2)
fsurf(sin(s), cos(s), t/10.*sin(1./s),'MeshDensity',40)
view(-172,25)
title('Increased MeshDensity = 40')

Figure contains 2 axes. Axes 1 with title Default MeshDensity = 35 contains an object of type parameterizedfunctionsurface. Axes 2 with title Increased MeshDensity = 40 contains an object of type parameterizedfunctionsurface.

Показать горизонтали под графиком поверхности

Отображение горизонталей для графика поверхности выражения f путем установки 'ShowContours' опция для 'on'.

syms x y
f = 3*(1-x)^2*exp(-(x^2)-(y+1)^2)...
- 10*(x/5 - x^3 - y^5)*exp(-x^2-y^2)...
- 1/3*exp(-(x+1)^2 - y^2);
fsurf(f,[-3 3],'ShowContours','on')

Figure contains an axes. The axes contains an object of type functionsurface.

Создание анимаций поверхностных графиков

Создание анимации путем изменения отображаемого выражения с помощью Function, XFunction, YFunction, и ZFunction свойства и затем с помощью drawnow для обновления графика. Сведения об экспорте в GIF см. в разделе imwrite.

Изменяя переменную i от 1 до 3, анимируйте параметрическую поверхность

$\begin{array}{l} x = tsin \\ (s) y = \\ cos (s \frac{)}{} z \end{array}$ = sin (is).

для -0,1 < u < 0,1 и 0 < v < 1. Увеличение скорости печати за счет уменьшения MeshDensity кому 9.

syms s t
h = fsurf(t.*sin(s), cos(s), sin(1./s), [-0.1 0.1 0 1]);
h.MeshDensity = 9;
for i=1:0.05:3
    h.ZFunction = sin(i./s);
    drawnow
end

Улучшение внешнего вида поверхностного графика

Создание символического выражения f для функции

$f = 3 (^{} 1-x) {2exp}^{} (- (x2)^{} - (y + 1)^{2})^{-} 10 (^{}^{} x/5-x3-y5) \exp (- {x2-y2}^{)} -^{}$ 1/3exp (- (x + 1) 2-y2).

Постройте график выражения f как поверхность. Улучшение внешнего вида графика поверхности с помощью свойств маркера перемещения, возвращаемого fsurf, свойства освещения и colormap.

Создание источника света с помощью camlight. Увеличение яркости с помощью brighten. Удалить линии по настройке EdgeColor кому 'none'. Увеличение внешнего освещения с помощью AmbientStrength. Дополнительные сведения см. в разделах Освещение, Прозрачность и Раскрашивание. Включите поле осей. Для заголовка преобразуйте f в LaTeX с использованием latex. Наконец, чтобы улучшить внешний вид засечек осей, меток осей и заголовка, задайте 'Interpreter' кому 'latex'.

syms x y
f = 3*(1-x)^2*exp(-(x^2)-(y+1)^2)... 
   - 10*(x/5 - x^3 - y^5)*exp(-x^2-y^2)... 
   - 1/3*exp(-(x+1)^2 - y^2);
h = fsurf(f,[-3 3]);

camlight(110,70)
brighten(0.6)
h.EdgeColor = 'none';
h.AmbientStrength = 0.4;

a = gca;
a.TickLabelInterpreter = 'latex';
a.Box = 'on';
a.BoxStyle = 'full';

xlabel('$x$','Interpreter','latex')
ylabel('$y$','Interpreter','latex')
zlabel('$z$','Interpreter','latex')
title_latex = ['$' latex(f) '$'];
title(title_latex,'Interpreter','latex')

$Figure contains an axes. The axes with title $3\,{\mathrm{e}}^{-{\left(y+1\right)}^2-x^2}\,{\left(x-1\right)}^2-\frac{{\mathrm{e}}^{-{\left(x+1\right)}^2-y^2}}{3}+{\mathrm{e}}^{-x^2-y^2}\,\left(10\,x^3-2\,x+10\,y^5\right)$ contains an object of type functionsurface.$

Печать поверхности с ограниченной плоскостью

Постройте график цилиндрической оболочки, ограниченной ниже плоскостью x-y и выше плоскостью $z = x$ + 2.

syms r t u
fsurf(cos(t),sin(t),u*(cos(t)+2),[0 2*pi 0 1])
hold on;

Добавьте график поверхности плоскости $z = x$ + 2.

fsurf(r*cos(t),r*sin(t),r*cos(t)+2,[0 1 0 2*pi])

Figure contains an axes. The axes contains 2 objects of type parameterizedfunctionsurface.

Применить поворот и перемещение к печати поверхности

Применение вращения и перемещения к графику поверхности тора.

Тор можно определить параметрически

$\begin{array}{l} x (θ, φ) = (R+a, потому что θ), потому что \\ φy (θ, φ) = (R+a, потому что θ) \\ грешат φz (θ, φ) =a \end{array}$ грех φ

где

$λ$ - полярный угол, а start- азимутальный угол
$a$ - радиус трубки;
$R$ - расстояние от центра трубы до центра тора;

Определите значения для $a$ и $R$ как 1 и 5 соответственно. Постройте график тора с помощью fsurf.

syms theta phi
a = 1;
R = 4;
x = (R + a*cos(theta))*cos(phi);
y = (R + a*cos(theta))*sin(phi);
z = a*sin(theta);
fsurf(x,y,z,[0 2*pi 0 2*pi])
hold on

Примените поворот к тору вокруг оси X. Определите матрицу поворота. Поверните тор на 90 градусов или $λ/2$ радиана.

alpha = pi/2;
Rx = [1 0 0;
      0 cos(alpha) -sin(alpha);
      0 sin(alpha) cos(alpha)];
r = [x; y; z];
r_90 = Rx*r;

Сместите центр тора на 5 вдоль оси X. Добавьте второй график повернутого и перемещенного тора к существующему графу.

fsurf(r_90(1)+5,r_90(2),r_90(3))
axis([-5 10 -5 10 -5 5])
hold off

Figure contains an axes. The axes contains 2 objects of type parameterizedfunctionsurface.

Входные аргументы

свернуть все

`f` - 3-D выражение или функцию для печати
символьное выражение | символьная функция

Выражение или функция для печати, заданная как символическое выражение или функция.

`[min max]` - Интервал печати для осей X и Y
[-5 5] (по умолчанию) | вектор из двух чисел

Интервал печати для осей X и Y, заданный как вектор из двух чисел. Значение по умолчанию: [-5 5].

`[xmin xmax ymin ymax]` - Интервал печати для осей X и Y
[-5 5 -5 5] (по умолчанию) | вектор из четырех чисел

Интервал печати для осей x и y, заданный как вектор из четырех чисел. Значение по умолчанию: [-5 5 -5 5].

`funx,funy,funz` - Параметрические функции `u` и `v`
символьные выражения | символьные функции

Параметрические функции u и v, указанное как символическое выражение или функция.

`[uvmin uvmax]` - Интервал печати для `u` и `v`
[-5 5] (по умолчанию) | вектор из двух чисел

Интервал печати для u и v оси, заданные как вектор из двух чисел. Значение по умолчанию: [-5 5].

`[umin umax vmin vmax]` - Интервал печати для `u` и `v`
[-5 5 -5 5] (по умолчанию) | вектор из четырех чисел

Интервал печати для u и v, заданный как вектор из четырех чисел. Значение по умолчанию: [-5 5 -5 5].

`ax` - Объект Axes
объект axes

Объект Axes. Если объект axes не указан, то fsurf использует текущие оси.

`LineSpec` - Стиль линии, маркер и цвет
символьный вектор | строка

Стиль линии, маркер и цвет, заданные как символьный вектор или строка, содержащая символы. Символы могут отображаться в любом порядке. Нет необходимости указывать все три признака (стиль линии, маркер и цвет). Например, если опустить стиль линии и указать маркер, на графике будет отображаться только маркер и ни одной линии.

Пример: '--or' - красная пунктирная линия с маркерами окружности

Стиль линии	Описание
`-`	Сплошная линия
`--`	Пунктирная линия
`:`	Пунктирная линия
`-.`	Черточно-точечная линия

Маркер	Описание
`'o'`	Круг
`'+'`	Знак «Плюс»
`'*'`	Звездочка
`'.'`	Пункт
`'x'`	Крест
`'_'`	Горизонтальная линия
`'\|'`	Вертикальная линия
`'s'`	Квадрат
`'d'`	Алмаз
`'^'`	Треугольник, направленный вверх
`'v'`	Треугольник, направленный вниз
`'>'`	Прямоугольный треугольник
`'<'`	Треугольник, указывающий влево
`'p'`	Пентаграмма
`'h'`	Hexagram

Цвет	Описание
`y`	желтый
`m`	пурпурный
`c`	голубой
`r`	красный
`g`	зеленый
`b`	синий
`w`	белый
`k`	черный

Аргументы пары «имя-значение»

Укажите дополнительные пары, разделенные запятыми Name,Value аргументы. Name является именем аргумента и Value - соответствующее значение. Name должен отображаться внутри кавычек. Можно указать несколько аргументов пары имен и значений в любом порядке как Name1,Value1,...,NameN,ValueN.

Пример: 'Marker','o','MarkerFaceColor','red'

Перечисленные здесь свойства являются только подмножеством. Полный список см. в разделе Функции Свойства поверхности.

`'MeshDensity'` - Количество точек оценки на направление
35 (по умолчанию) | число

Количество точек оценки на направление, указанное как число. Значение по умолчанию: 35. Поскольку fsurf объекты используют адаптивную оценку, фактическое количество точек оценки больше.

Пример: 100

`'ShowContours'` - Отображение контурного графика на графике
`'off'` (по умолчанию) | логическое значение on/off

Отображать контурный график на графике, указанный как 'on' или 'off'или как числовое или логическое 1 (true) или 0 (false). Значение 'on' эквивалентно true, и 'off' эквивалентно false. Таким образом, можно использовать значение этого свойства в качестве логического значения. Значение сохраняется как логическое значение типа вкл/выкл matlab.lang.OnOffSwitchState.

`'EdgeColor'` - Цвет линии
`[0 0 0]` (по умолчанию) | `'interp'` | Триплет RGB | шестнадцатеричный цветовой код | `'r'` | `'g'` | `'b'` | ...

Цвет линии, указан как 'interp', триплет RGB, шестнадцатеричный цветовой код, имя цвета или короткое имя. Значение триплета RGB по умолчанию [0 0 0] соответствует черному. 'interp' значение цветит края на основе ZData значения.

Для пользовательского цвета укажите триплет RGB или шестнадцатеричный цветовой код.

Триплет RGB - это трехэлементный вектор строки, элементы которого задают интенсивности красной, зеленой и синей составляющих цвета. Интенсивности должны находиться в диапазоне [0,1]; например, [0.4 0.6 0.7].
Шестнадцатеричный цветовой код - это символьный вектор или строковый скаляр, начинающийся с хэш-символа (#), за которыми следуют три или шесть шестнадцатеричных цифр, которые могут варьироваться от 0 кому F. Значения не чувствительны к регистру. Таким образом, цветовые коды '#FF8800', '#ff8800', '#F80', и '#f80' эквивалентны.

Можно также задать некоторые общие цвета по имени. В этой таблице перечислены параметры именованного цвета, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.

Имя цвета	Краткое имя	Триплет RGB	Шестнадцатеричный цветовой код	Внешность
`'red'`	`'r'`	`[1 0 0]`	`'#FF0000'`
`'green'`	`'g'`	`[0 1 0]`	`'#00FF00'`
`'blue'`	`'b'`	`[0 0 1]`	`'#0000FF'`
`'cyan'`	`'c'`	`[0 1 1]`	`'#00FFFF'`
`'magenta'`	`'m'`	`[1 0 1]`	`'#FF00FF'`
`'yellow'`	`'y'`	`[1 1 0]`	`'#FFFF00'`
`'black'`	`'k'`	`[0 0 0]`	`'#000000'`
`'white'`	`'w'`	`[1 1 1]`	`'#FFFFFF'`
`'none'`	Неприменимо	Неприменимо	Неприменимо	Без цвета

Вот триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию MATLAB ®, используемых на многих типах графиков.

Триплет RGB	Шестнадцатеричный цветовой код	Внешность
`[0 0.4470 0.7410]`	`'#0072BD'`
`[0.8500 0.3250 0.0980]`	`'#D95319'`
`[0.9290 0.6940 0.1250]`	`'#EDB120'`
`[0.4940 0.1840 0.5560]`	`'#7E2F8E'`
`[0.4660 0.6740 0.1880]`	`'#77AC30'`
`[0.3010 0.7450 0.9330]`	`'#4DBEEE'`
`[0.6350 0.0780 0.1840]`	`'#A2142F'`

`'LineStyle'` - Стиль линии
`'-'` (по умолчанию) | `'--'` | `':'` | `'-.'` | `'none'`

Стиль линии, указанный в качестве одного из параметров, перечисленных в этой таблице.

Стиль линии	Описание	Результирующая линия
`'-'`	Сплошная линия
`'--'`	Пунктирная линия
`':'`	Пунктирная линия
`'-.'`	Пунктирная линия
`'none'`	Без строки	Без строки

`'LineWidth'` - Ширина линии
`0.5` (по умолчанию) | положительное значение

Ширина линии, заданная как положительное значение в точках, где 1 точка = 1/72 дюйма. Если линия имеет маркеры, то ширина линии также влияет на кромки маркера.

Ширина линии не может быть меньше ширины пикселя. Если задать для ширины линии значение, меньшее, чем ширина пикселя в системе, линия будет отображаться в виде одного пикселя в ширину.

`'Marker'` - Символ маркера
`'none'` (по умолчанию) | `'o'` | `'+'` | `'*'` | `'.'` | ...

Символ маркера, указанный как одно из значений, перечисленных в этой таблице. По умолчанию объект не отображает маркеры. Задание обозначения маркера добавляет маркеры в каждую точку данных или вершину.

Стоимость	Описание
`'o'`	Круг
`'+'`	Знак «Плюс»
`'*'`	Звездочка
`'.'`	Пункт
`'x'`	Крест
`'_'`	Горизонтальная линия
`'\|'`	Вертикальная линия
`'square'` или `'s'`	Квадрат
`'diamond'` или `'d'`	Алмаз
`'^'`	Треугольник, направленный вверх
`'v'`	Треугольник, направленный вниз
`'>'`	Прямоугольный треугольник
`'<'`	Треугольник, указывающий влево
`'pentagram'` или `'p'`	Пятиконечная звезда (пентаграмма)
`'hexagram'` или `'h'`	Шестиконечная звезда (гексаграмма)
`'none'`	Без маркеров

`'MarkerEdgeColor'` - Цвет контура маркера
`'auto'` (по умолчанию) | триплет RGB | шестнадцатеричный цветовой код | `'r'` | `'g'` | `'b'` | ...

Цвет контура маркера, указанный как 'auto', триплет RGB, шестнадцатеричный цветовой код, имя цвета или короткое имя. Значение по умолчанию 'auto' использует тот же цвет, что и EdgeColor собственность.

Для пользовательского цвета укажите триплет RGB или шестнадцатеричный цветовой код.

Триплет RGB - это трехэлементный вектор строки, элементы которого задают интенсивности красной, зеленой и синей составляющих цвета. Интенсивности должны находиться в диапазоне [0,1]; например, [0.4 0.6 0.7].
Шестнадцатеричный цветовой код - это символьный вектор или строковый скаляр, начинающийся с хэш-символа (#), за которыми следуют три или шесть шестнадцатеричных цифр, которые могут варьироваться от 0 кому F. Значения не чувствительны к регистру. Таким образом, цветовые коды '#FF8800', '#ff8800', '#F80', и '#f80' эквивалентны.

Имя цвета	Краткое имя	Триплет RGB	Шестнадцатеричный цветовой код	Внешность
`'red'`	`'r'`	`[1 0 0]`	`'#FF0000'`
`'green'`	`'g'`	`[0 1 0]`	`'#00FF00'`
`'blue'`	`'b'`	`[0 0 1]`	`'#0000FF'`
`'cyan'`	`'c'`	`[0 1 1]`	`'#00FFFF'`
`'magenta'`	`'m'`	`[1 0 1]`	`'#FF00FF'`
`'yellow'`	`'y'`	`[1 1 0]`	`'#FFFF00'`
`'black'`	`'k'`	`[0 0 0]`	`'#000000'`
`'white'`	`'w'`	`[1 1 1]`	`'#FFFFFF'`
`'none'`	Неприменимо	Неприменимо	Неприменимо	Без цвета

Вот триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию MATLAB, используемых на многих типах графиков.

Триплет RGB	Шестнадцатеричный цветовой код	Внешность
`[0 0.4470 0.7410]`	`'#0072BD'`
`[0.8500 0.3250 0.0980]`	`'#D95319'`
`[0.9290 0.6940 0.1250]`	`'#EDB120'`
`[0.4940 0.1840 0.5560]`	`'#7E2F8E'`
`[0.4660 0.6740 0.1880]`	`'#77AC30'`
`[0.3010 0.7450 0.9330]`	`'#4DBEEE'`
`[0.6350 0.0780 0.1840]`	`'#A2142F'`

Пример: [0.5 0.5 0.5]

Пример: 'blue'

Пример: '#D2F9A7'

`'MarkerFaceColor'` - Цвет заливки маркера
`'none'` (по умолчанию) | `'auto'` | Триплет RGB | шестнадцатеричный цветовой код | `'r'` | `'g'` | `'b'` | ...

Цвет заливки маркера, указанный как 'auto', триплет RGB, шестнадцатеричный цветовой код, имя цвета или короткое имя. 'auto' значение использует тот же цвет, что и MarkerEdgeColor собственность.

Для пользовательского цвета укажите триплет RGB или шестнадцатеричный цветовой код.

Триплет RGB - это трехэлементный вектор строки, элементы которого задают интенсивности красной, зеленой и синей составляющих цвета. Интенсивности должны находиться в диапазоне [0,1]; например, [0.4 0.6 0.7].
Шестнадцатеричный цветовой код - это символьный вектор или строковый скаляр, начинающийся с хэш-символа (#), за которыми следуют три или шесть шестнадцатеричных цифр, которые могут варьироваться от 0 кому F. Значения не чувствительны к регистру. Таким образом, цветовые коды '#FF8800', '#ff8800', '#F80', и '#f80' эквивалентны.

Имя цвета	Краткое имя	Триплет RGB	Шестнадцатеричный цветовой код	Внешность
`'red'`	`'r'`	`[1 0 0]`	`'#FF0000'`
`'green'`	`'g'`	`[0 1 0]`	`'#00FF00'`
`'blue'`	`'b'`	`[0 0 1]`	`'#0000FF'`
`'cyan'`	`'c'`	`[0 1 1]`	`'#00FFFF'`
`'magenta'`	`'m'`	`[1 0 1]`	`'#FF00FF'`
`'yellow'`	`'y'`	`[1 1 0]`	`'#FFFF00'`
`'black'`	`'k'`	`[0 0 0]`	`'#000000'`
`'white'`	`'w'`	`[1 1 1]`	`'#FFFFFF'`
`'none'`	Неприменимо	Неприменимо	Неприменимо	Без цвета

Триплет RGB	Шестнадцатеричный цветовой код	Внешность
`[0 0.4470 0.7410]`	`'#0072BD'`
`[0.8500 0.3250 0.0980]`	`'#D95319'`
`[0.9290 0.6940 0.1250]`	`'#EDB120'`
`[0.4940 0.1840 0.5560]`	`'#7E2F8E'`
`[0.4660 0.6740 0.1880]`	`'#77AC30'`
`[0.3010 0.7450 0.9330]`	`'#4DBEEE'`
`[0.6350 0.0780 0.1840]`	`'#A2142F'`

Пример: [0.3 0.2 0.1]

Пример: 'green'

Пример: '#D2F9A7'

`'MarkerSize'` - Размер маркера
`6` (по умолчанию) | положительное значение

Размер маркера, заданный как положительное значение в точках, где 1 точка = 1/72 дюйма.

Выходные аргументы

свернуть все

`fs` - Один или несколько объектов
скаляр | вектор

Один или несколько объектов, возвращаемых как скаляр или вектор. Объект является либо функциональным объектом поверхности, либо параметризованным объектом поверхности в зависимости от типа графика. Эти объекты можно использовать для запроса и изменения свойств определенной строки. Дополнительные сведения см. в разделах Функции Свойства поверхности и Параметры Функции Свойства поверхности.

Алгоритмы

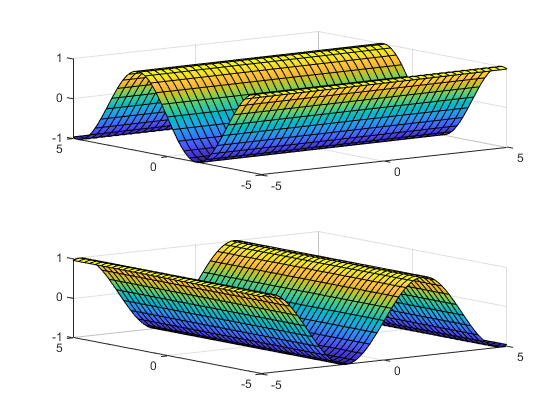
fsurf назначает символьные переменные в f в x ось, затем y ось, и symvar определяет порядок присваиваемых переменных. Поэтому имена переменных и осей могут не соответствовать друг другу. Вызвать fsurf чтобы назначить х или у соответствующей оси, создайте символическую функцию для печати, затем передайте символическую функцию в fsurf.

Например, следующие графики кода f (x, y) = sin (y) двумя способами. Первый путь заставляет волны колебаться относительно оси y. Второй способ присваивает оси x значение y, поскольку это первая (и единственная) переменная в символьной функции.

syms x y;
f(x,y) = sin(y);

figure;
subplot(2,1,1)
fsurf(f);
subplot(2,1,2)
fsurf(f(x,y)); % Or fsurf(sin(y));

См. также

Представлен в R2016a

Документация

fsurf

Синтаксис

Описание

Примеры

3-D График поверхности символьного выражения

3-D График поверхности символьной функции

Задание интервала печати поверхности

Параметризованный график поверхности

График поверхности кусочного выражения

Добавление меток заголовка и оси и засечек формата

Стиль и ширина линий для печати поверхности

Изменить поверхность после создания

Графики нескольких поверхностей и прозрачные поверхности

Управляющее разрешение поверхностного графика

Показать горизонтали под графиком поверхности

Создание анимаций поверхностных графиков

Улучшение внешнего вида поверхностного графика

Печать поверхности с ограниченной плоскостью

Применить поворот и перемещение к печати поверхности

Входные аргументы

f - 3-D выражение или функцию для печати символьное выражение | символьная функция

[min max] - Интервал печати для осей X и Y [-5 5] (по умолчанию) | вектор из двух чисел

[xmin xmax ymin ymax] - Интервал печати для осей X и Y [-5 5 -5 5] (по умолчанию) | вектор из четырех чисел

funx,funy,funz - Параметрические функции u и v символьные выражения | символьные функции

[uvmin uvmax] - Интервал печати для u и v [-5 5] (по умолчанию) | вектор из двух чисел

[umin umax vmin vmax] - Интервал печати для u и v [-5 5 -5 5] (по умолчанию) | вектор из четырех чисел

ax - Объект Axes объект axes

LineSpec - Стиль линии, маркер и цвет символьный вектор | строка

Аргументы пары «имя-значение»

'MeshDensity' - Количество точек оценки на направление 35 (по умолчанию) | число

'ShowContours' - Отображение контурного графика на графике 'off' (по умолчанию) | логическое значение on/off

'EdgeColor' - Цвет линии [0 0 0] (по умолчанию) | 'interp' | Триплет RGB | шестнадцатеричный цветовой код | 'r' | 'g' | 'b' | ...

'LineStyle' - Стиль линии '-' (по умолчанию) | '--' | ':' | '-.' | 'none'

'LineWidth' - Ширина линии 0.5 (по умолчанию) | положительное значение

'Marker' - Символ маркера 'none' (по умолчанию) | 'o' | '+' | '*' | '.' | ...

'MarkerEdgeColor' - Цвет контура маркера 'auto' (по умолчанию) | триплет RGB | шестнадцатеричный цветовой код | 'r' | 'g' | 'b' | ...

'MarkerFaceColor' - Цвет заливки маркера 'none' (по умолчанию) | 'auto' | Триплет RGB | шестнадцатеричный цветовой код | 'r' | 'g' | 'b' | ...

'MarkerSize' - Размер маркера 6 (по умолчанию) | положительное значение

Выходные аргументы

fs - Один или несколько объектов скаляр | вектор

Алгоритмы

См. также

Функции

Свойства

Темы

Документация по инструментам символьной математики

Поддержка

`f` - 3-D выражение или функцию для печати
символьное выражение | символьная функция

`[min max]` - Интервал печати для осей X и Y
[-5 5] (по умолчанию) | вектор из двух чисел

`[xmin xmax ymin ymax]` - Интервал печати для осей X и Y
[-5 5 -5 5] (по умолчанию) | вектор из четырех чисел

`funx,funy,funz` - Параметрические функции `u` и `v`
символьные выражения | символьные функции

`[uvmin uvmax]` - Интервал печати для `u` и `v`
[-5 5] (по умолчанию) | вектор из двух чисел

`[umin umax vmin vmax]` - Интервал печати для `u` и `v`
[-5 5 -5 5] (по умолчанию) | вектор из четырех чисел

`ax` - Объект Axes
объект axes

`LineSpec` - Стиль линии, маркер и цвет
символьный вектор | строка

`'MeshDensity'` - Количество точек оценки на направление
35 (по умолчанию) | число

`'ShowContours'` - Отображение контурного графика на графике
`'off'` (по умолчанию) | логическое значение on/off

`'EdgeColor'` - Цвет линии
`[0 0 0]` (по умолчанию) | `'interp'` | Триплет RGB | шестнадцатеричный цветовой код | `'r'` | `'g'` | `'b'` | ...

`'LineStyle'` - Стиль линии
`'-'` (по умолчанию) | `'--'` | `':'` | `'-.'` | `'none'`

`'LineWidth'` - Ширина линии
`0.5` (по умолчанию) | положительное значение

`'Marker'` - Символ маркера
`'none'` (по умолчанию) | `'o'` | `'+'` | `'*'` | `'.'` | ...

`'MarkerEdgeColor'` - Цвет контура маркера
`'auto'` (по умолчанию) | триплет RGB | шестнадцатеричный цветовой код | `'r'` | `'g'` | `'b'` | ...

`'MarkerFaceColor'` - Цвет заливки маркера
`'none'` (по умолчанию) | `'auto'` | Триплет RGB | шестнадцатеричный цветовой код | `'r'` | `'g'` | `'b'` | ...

`'MarkerSize'` - Размер маркера
`6` (по умолчанию) | положительное значение

`fs` - Один или несколько объектов
скаляр | вектор