Формируйте регулятор с учетом состояния-обратной связи и усиления оценщика
rsys = reg(sys,K,L)
rsys = reg(sys,K,L,sensors,known,controls)
rsys = reg(sys,K,L) образует динамический регулятор или компенсатор rsys заданную модель пространства состояний sys объекта, матрица усиления с обратной связью Kи оценочную матрицу усиления L. Коэффициент усиления K и L обычно спроектированы с использованием методов размещения полюсов или LQG. Функция reg обрабатывает случаи как непрерывного, так и дискретного времени.
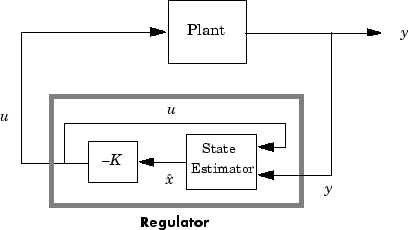
Этот синтаксис принимает, что все входы sys являются элементами управления, и все выходы измеряются. Регулятор rsys получается путем соединения закона обратной связи состояний u = - Kx и оценки состояния с матрицей усиления L (см. estim). Для объекта с уравнениями
это приводит к регулятору
Этот регулятор должен быть подключен к объекту с помощью положительной обратной связи.
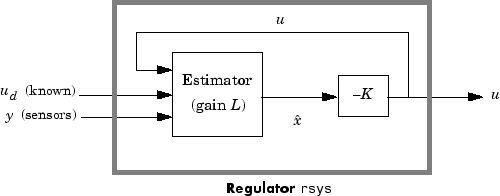
rsys = reg(sys,K,L,sensors,known,controls) решает более общие проблемы регулирования, где:
Входы объекта управления состоят из u элементов управления, известных входов ud и стохастических входов w.
Измеряется только подмножество y выходов объекта управления.
Векторы индекса sensors, known, и controls задайте y, ud и u как подмножества выходов и входов sys. Получившийся регулятор использует [ud; y] как входы для генерации команд u (см. Следующий рисунок).
Учитывая модель пространства состояний в непрерывном времени
sys = ss(A,B,C,D)
с семью выходами и четырьмя входами, предположим, что вы разработали:
Коэффициент усиления контроллера обратной связи K использование входов 1, 2 и 4 объекта в качестве входов управления
Оценщик состояния с L усиления использование выходов 4, 7 и 1 объекта в качестве датчиков и вход 3 объекта в качестве дополнительного известного входа
Затем можно подключить контроллер и оценщик и сформировать полную систему регулирования путем
controls = [1,2,4]; sensors = [4,7,1]; known = [3]; regulator = reg(sys,K,L,sensors,known,controls)