Выполните выбор переменной предиктора для байесовских линейных регрессионых моделей
Чтобы оценить апостериорное распределение стандартной байесовской линейной регрессионой модели, см. estimate.
PosteriorMdl = estimate(PriorMdl,X,y)estimate также выполняет выбор переменной предиктора.
PriorMdl задает предшествующее распределение параметров в соединении, структуру линейной регрессионой модели и алгоритм выбора переменных. X - данные предиктора и y - данные отклика. PriorMdl и PosteriorMdl являются не совпадающими типами объектов.
Для создания PosteriorMdl, estimate обновляет предшествующее распределение информацией о параметрах, которые он получает из данных.
NaNs в данных указывают отсутствующие значения, которые estimate удаляет с помощью спискового удаления.
PosteriorMdl = estimate(PriorMdl,X,y,Name,Value)'Lambda',0.5 задает, что значение параметров усадки для регрессии Байесова лассо 0.5 для всех коэффициентов, кроме точки пересечения.
Если вы задаете Beta или Sigma2, затем PosteriorMdl и PriorMdl равны.
[ использует любую из комбинаций входных аргументов в предыдущих синтаксисах, а также возвращает таблицу, которая включает следующее для каждого параметра: апостериорные оценки, стандартные ошибки, 95% доверительные интервалы и апостериорную вероятность того, что параметр больше 0.PosteriorMdl,Summary]
= estimate(___)
Рассмотрим множественную линейную регрессионую модель, которая предсказывает реальный валовой национальный продукт США (GNPR) с использованием линейной комбинации индекса промышленного производства (IPI), общая занятость (E), и реальная заработная плата (WR).
Для всех , - серия независимых гауссовских нарушений порядка со средним значением 0 и отклонением .
Предположим, что предыдущие распределения:
Для k = 0,..., 3 , имеет распределение Laplace со средним значением 0 и шкалой , где - параметр усадки. Коэффициенты являются условно независимыми.
. и - форма и шкала, соответственно, обратного гамма- распределения.
Создайте предыдущую модель регрессии лассо Байеса. Задайте количество предикторов, тип предыдущей модели и имена переменных. Задайте следующие усадки:
0.01 для точки пересечения
10 для IPI и WR
1e5 для E потому что он имеет шкалу, которая на несколько порядков величины больше, чем другие переменные
Порядок усадок соответствует порядку заданных имен переменных, но первый элемент является усадкой точки пересечения.
p = 3; PriorMdl = bayeslm(p,'ModelType','lasso','Lambda',[0.01; 10; 1e5; 10],... 'VarNames',["IPI" "E" "WR"]);
PriorMdl является lassoblm Байесовский объект линейной регрессионной модели, представляющий предшествующее распределение коэффициентов регрессии и отклонение нарушения порядка.
Загрузите набор данных Нельсона-Плоссера. Создайте переменные для ряда отклика и предиктора.
load Data_NelsonPlosser X = DataTable{:,PriorMdl.VarNames(2:end)}; y = DataTable{:,"GNPR"};
Выполните регрессию байесовского лассо, передав предыдущую модель и данные в estimate, то есть путем оценки апостериорного распределения и . Байесовская регрессия лассо использует марковскую цепь Monte Carlo (MCMC) для выборки из апостериорной. Для воспроизводимости установите случайный seed.
rng(1); PosteriorMdl = estimate(PriorMdl,X,y);
Method: lasso MCMC sampling with 10000 draws
Number of observations: 62
Number of predictors: 4
| Mean Std CI95 Positive Distribution
-------------------------------------------------------------------------
Intercept | -1.3472 6.8160 [-15.169, 11.590] 0.427 Empirical
IPI | 4.4755 0.1646 [ 4.157, 4.799] 1.000 Empirical
E | 0.0001 0.0002 [-0.000, 0.000] 0.796 Empirical
WR | 3.1610 0.3136 [ 2.538, 3.760] 1.000 Empirical
Sigma2 | 60.1452 11.1180 [42.319, 85.085] 1.000 Empirical
PosteriorMdl является empiricalblm объект модели, который хранит черты из апостериорных распределений и учитывая данные. estimate отображает сводные данные маргинальных апостериорных распределений в командной строке MATLAB ®. Строки сводных данных соответствуют коэффициентам регрессии и нарушения порядка отклонения, а столбцы соответствуют характеристикам апостериорного распределения. Характеристики включают:
CI95, который содержит 95% байесовских справедливых интервалов для параметров. Для примера апостериорная вероятность того, что коэффициент регрессии IPI находится в [4.157, 4.799] 0,95.
Positive, который содержит апостериорную вероятность того, что параметр больше 0. Для примера вероятность того, что точка пересечения больше 0, 0.427.
Постройте график апостериорных распределений.
plot(PosteriorMdl)

Учитывая усадку, распределение E довольно плотный около 0. Поэтому E возможно, не является важным предиктором.
По умолчанию estimate рисует и отбрасывает сгорающую выборку размера 5000. Однако передовой практикой является проверка следового графика рисок на предмет адекватного смешивания и отсутствия переходного процесса. Постройте график трассировки рисунков для каждого параметра. Вы можете получить доступ к рисункам, которые составляют распределение (свойства BetaDraws и Sigma2Draws) с использованием записи через точку.
figure; for j = 1:(p + 1) subplot(2,2,j); plot(PosteriorMdl.BetaDraws(j,:)); title(sprintf('%s',PosteriorMdl.VarNames{j})); end

figure;
plot(PosteriorMdl.Sigma2Draws);
title('Sigma2');
Графики следов показывают, что рисунки, кажется, хорошо смешиваются. Графики не показывают обнаруживаемой переходности или последовательной корреляции, и рисунки не скачут между состояниями.
Рассмотрим регрессионую модель в Выборе Переменных с Использованием Регрессии Бейесова Лассо.
Создайте предыдущую модель для выполнения выбора переменной стохастического поиска (SSVS). Предположим, что и являются зависимыми (модель сопряженной смеси). Задайте количество предикторов p и имена коэффициентов регрессии.
p = 3; PriorMdl = mixconjugateblm(p,'VarNames',["IPI" "E" "WR"]);
Загрузите набор данных Нельсона-Плоссера. Создайте переменные для ряда отклика и предиктора.
load Data_NelsonPlosser X = DataTable{:,PriorMdl.VarNames(2:end)}; y = DataTable{:,'GNPR'};
Реализуйте SSVS путем оценки маргинальных апостериорных распределений и . Поскольку SSVS использует Марков цепь Монте-Карло для оценки, установите seed случайных чисел, чтобы воспроизвести результаты.
rng(1); PosteriorMdl = estimate(PriorMdl,X,y);
Method: MCMC sampling with 10000 draws
Number of observations: 62
Number of predictors: 4
| Mean Std CI95 Positive Distribution Regime
----------------------------------------------------------------------------------
Intercept | -18.8333 10.1851 [-36.965, 0.716] 0.037 Empirical 0.8806
IPI | 4.4554 0.1543 [ 4.165, 4.764] 1.000 Empirical 0.4545
E | 0.0010 0.0004 [ 0.000, 0.002] 0.997 Empirical 0.0925
WR | 2.4686 0.3615 [ 1.766, 3.197] 1.000 Empirical 0.1734
Sigma2 | 47.7557 8.6551 [33.858, 66.875] 1.000 Empirical NaN
PosteriorMdl является empiricalblm объект модели, который хранит черты из апостериорных распределений и учитывая данные. estimate отображает сводные данные маргинальных апостериорных распределений в командной строке. Строки сводных данных соответствуют коэффициентам регрессии и нарушения порядка отклонения, а столбцы соответствуют характеристикам апостериорного распределения. Характеристики включают:
CI95, который содержит 95% байесовских справедливых интервалов для параметров. Для примера апостериорная вероятность того, что коэффициент регрессии E (стандартизированный) находится в [0,000, 0,0,002] в 0,95.
Regime, который содержит маргинальную апостериорную вероятность переменного включения ( для переменной). Для примера - апостериорная вероятность E который должен быть включен в модель 0,0925.
Принимая, что переменные с Regime < 0,1 следует удалить из модели, результаты показывают, что можно исключить уровень безработицы из модели.
По умолчанию estimate рисует и отбрасывает сгорающую выборку размера 5000. Однако передовой практикой является проверка следового графика рисок на предмет адекватного смешивания и отсутствия переходного процесса. Постройте график трассировки рисунков для каждого параметра. Вы можете получить доступ к рисункам, которые составляют распределение (свойства BetaDraws и Sigma2Draws) с использованием записи через точку.
figure; for j = 1:(p + 1) subplot(2,2,j); plot(PosteriorMdl.BetaDraws(j,:)); title(sprintf('%s',PosteriorMdl.VarNames{j})); end

figure;
plot(PosteriorMdl.Sigma2Draws);
title('Sigma2');
Графики следов показывают, что рисунки, кажется, хорошо смешиваются. Графики не показывают обнаруживаемой переходности или последовательной корреляции, и рисунки не скачут между состояниями.
Рассмотрим регрессионую модель и предшествующее распределение в Select Variables Using Bayesian Lasso Regression.
Создайте байесову регрессию лассо предыдущую модель для 3 предикторов и задайте имена переменных. Задайте значения усадки 0.01, 10, 1e5, и 10 для точки пересечения и коэффициентов IPI, E, и WR.
p = 3; PriorMdl = bayeslm(p,'ModelType','lasso','VarNames',["IPI" "E" "WR"],... 'Lambda',[0.01; 10; 1e5; 10]);
Загрузите набор данных Нельсона-Плоссера. Создайте переменные для ряда отклика и предиктора.
load Data_NelsonPlosser X = DataTable{:,PriorMdl.VarNames(2:end)}; y = DataTable{:,"GNPR"};
Оцените условное апостериорное распределение учитывая данные и что и возвращает сводную таблицу оценок для доступа к оценкам.
rng(1); % For reproducibility [Mdl,SummaryBeta] = estimate(PriorMdl,X,y,'Sigma2',10);
Method: lasso MCMC sampling with 10000 draws
Conditional variable: Sigma2 fixed at 10
Number of observations: 62
Number of predictors: 4
| Mean Std CI95 Positive Distribution
------------------------------------------------------------------------
Intercept | -8.0643 4.1992 [-16.384, 0.018] 0.025 Empirical
IPI | 4.4454 0.0679 [ 4.312, 4.578] 1.000 Empirical
E | 0.0004 0.0002 [ 0.000, 0.001] 0.999 Empirical
WR | 2.9792 0.1672 [ 2.651, 3.305] 1.000 Empirical
Sigma2 | 10 0 [10.000, 10.000] 1.000 Empirical
estimate отображает сводные данные условного апостериорного распределения . Поскольку фиксируется на 10 во время оценки, выводы на ней тривиальны.
Отобразите Mdl.
Mdl
Mdl =
lassoblm with properties:
NumPredictors: 3
Intercept: 1
VarNames: {4x1 cell}
Lambda: [4x1 double]
A: 3
B: 1
| Mean Std CI95 Positive Distribution
---------------------------------------------------------------------------
Intercept | 0 100 [-200.000, 200.000] 0.500 Scale mixture
IPI | 0 0.1000 [-0.200, 0.200] 0.500 Scale mixture
E | 0 0.0000 [-0.000, 0.000] 0.500 Scale mixture
WR | 0 0.1000 [-0.200, 0.200] 0.500 Scale mixture
Sigma2 | 0.5000 0.5000 [ 0.138, 1.616] 1.000 IG(3.00, 1)
Потому что estimate вычисляет условное апостериорное распределение, оно возвращает входной параметр модели PriorMdl, не условный апостериор, в первой позиции списка выходных аргументов.
Отобразите сводную таблицу оценок.
SummaryBeta
SummaryBeta=5×6 table
Mean Std CI95 Positive Distribution Covariances
__________ __________ ________________________ ________ _____________ _______________________________________________________________________
Intercept -8.0643 4.1992 -16.384 0.01837 0.0254 {'Empirical'} 17.633 0.17621 -0.00053724 0.11705 0
IPI 4.4454 0.067949 4.312 4.5783 1 {'Empirical'} 0.17621 0.0046171 -1.4103e-06 -0.0068855 0
E 0.00039896 0.00015673 9.4925e-05 0.00070697 0.9987 {'Empirical'} -0.00053724 -1.4103e-06 2.4564e-08 -1.8168e-05 0
WR 2.9792 0.16716 2.6506 3.3046 1 {'Empirical'} 0.11705 -0.0068855 -1.8168e-05 0.027943 0
Sigma2 10 0 10 10 1 {'Empirical'} 0 0 0 0 0
SummaryBeta содержит условные апостериорные оценки.
Оцените условные апостериорные распределения учитывая, что - условное апостериорное среднее значение (хранится в SummaryBeta.Mean(1:(end – 1))). Верните сводную таблицу оценок.
condPostMeanBeta = SummaryBeta.Mean(1:(end - 1));
[~,SummarySigma2] = estimate(PriorMdl,X,y,'Beta',condPostMeanBeta);Method: lasso MCMC sampling with 10000 draws
Conditional variable: Beta fixed at -8.0643 4.4454 0.00039896 2.9792
Number of observations: 62
Number of predictors: 4
| Mean Std CI95 Positive Distribution
------------------------------------------------------------------------
Intercept | -8.0643 0.0000 [-8.064, -8.064] 0.000 Empirical
IPI | 4.4454 0.0000 [ 4.445, 4.445] 1.000 Empirical
E | 0.0004 0.0000 [ 0.000, 0.000] 1.000 Empirical
WR | 2.9792 0.0000 [ 2.979, 2.979] 1.000 Empirical
Sigma2 | 56.8314 10.2921 [39.947, 79.731] 1.000 Empirical
estimate отображает сводные данные оценок условного апостериорного распределения учитывая данные и что является condPostMeanBeta. На отображении выводы тривиальны.
Рассмотрим регрессионую модель в Выборе Переменных с Использованием Регрессии Бейесова Лассо.
Создайте предыдущую модель для выполнения SSVS. Предположим, что и являются зависимыми (модель сопряженной смеси). Задайте количество предикторов p и имена коэффициентов регрессии.
p = 3; PriorMdl = mixconjugateblm(p,'VarNames',["IPI" "E" "WR"]);
Загрузите набор данных Нельсона-Плоссера. Создайте переменные для ряда отклика и предиктора.
load Data_NelsonPlosser X = DataTable{:,PriorMdl.VarNames(2:end)}; y = DataTable{:,'GNPR'};
Реализуйте SSVS путем оценки маргинальных апостериорных распределений и . Поскольку SSVS использует Марков цепь Монте-Карло для оценки, установите seed случайных чисел, чтобы воспроизвести результаты. Подавьте отображение оценки, но верните сводную таблицу оценки.
rng(1);
[PosteriorMdl,Summary] = estimate(PriorMdl,X,y,'Display',false);PosteriorMdl является empiricalblm объект модели, который хранит черты из апостериорных распределений и учитывая данные. Summary - таблица со столбцами, соответствующими апостериорным характеристикам, и строками, соответствующими коэффициентам (PosteriorMdl.VarNames) и отклонение нарушения порядка (Sigma2).
Отобразите оцененную ковариационную матрицу параметра (Covariances) и доля раз, в которую алгоритм включает каждый предиктор (Regime).
Covariances = Summary(:,"Covariances")Covariances=5×1 table
Covariances
______________________________________________________________________
Intercept 103.74 1.0486 -0.0031629 0.6791 7.3916
IPI 1.0486 0.023815 -1.3637e-05 -0.030387 0.06611
E -0.0031629 -1.3637e-05 1.3481e-07 -8.8792e-05 -0.00025044
WR 0.6791 -0.030387 -8.8792e-05 0.13066 0.089039
Sigma2 7.3916 0.06611 -0.00025044 0.089039 74.911
Regime = Summary(:,"Regime")Regime=5×1 table
Regime
______
Intercept 0.8806
IPI 0.4545
E 0.0925
WR 0.1734
Sigma2 NaN
Regime содержит предельную апостериорную вероятность включения переменной ( для переменной). Для примера, апостериорная вероятность того, что E должен быть включен в модель 0,0925.
Принимая, что переменные с Regime < 0,1 следует удалить из модели, результаты показывают, что можно исключить уровень безработицы из модели.
PriorMdl - Байесовская линейная регрессионая модель для выбора переменной предиктораmixconjugateblm объект модели | mixsemiconjugateblm объект модели | lassoblm объект моделиБайесовская линейная регрессионая модель для выбора переменной предиктора, заданная как объект модели в этой таблице.
| Объект модели | Описание |
|---|---|
mixconjugateblm | Зависимая, Гауссовская гамма инверсии смеси спрягает модель для выбора переменной предсказателя SSVS, возвращенного bayeslm |
mixsemiconjugateblm | Независимая, Гауссова-смесь-обратная-гамма полуконъюгатная модель для выбора переменной предиктора SSVS, возвращенная bayeslm |
lassoblm | Байесовская регрессионая модель лассо, возвращенная bayeslm |
X - Данные предиктораДанные предиктора для многофакторной линейной регрессии, заданные как numObservations-by- PriorMdl.NumPredictors числовая матрица. numObservations количество наблюдений и должно быть равно длине y.
Типы данных: double
y - Данные откликаДанные отклика для многофакторной линейной регрессии, заданные как числовой вектор с numObservations элементы.
Типы данных: double
Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.
'Sigma2',2 задает оценку условного апостериорного распределения коэффициентов регрессии с учетом данных и что заданное отклонение нарушения порядка 2.'Display' - Флаг для отображения сводных данных байесовских оценок в командной строкеtrue (по умолчанию) | falseФлаг для отображения сводных данных байесовских оценок в командной строке, заданный как разделенная разделенными запятой парами, состоящая из 'Display' и значение в этой таблице.
| Значение | Описание |
|---|---|
true | estimate печатает информацию оценки и таблицу, суммирующую байесовские оценки в командную строку. |
false | estimate не печатается в командной строке. |
Информация об оценке включает в себя способ оценки, фиксированные параметры, количество наблюдений и количество предикторов. Итоговая таблица содержит предполагаемые апостериорные средства, стандартные отклонения (квадратный корень апостериорной дисперсии), 95% справедливых достоверных интервалов, апостериорную вероятность того, что параметр больше 0, и описание апостериорного распределения (если известно). Для моделей, которые выполняют SSVS, таблица отображения включает столбец для вероятностей включения переменной.
Если вы задаете Beta или Sigma2, затем estimate включает вашу спецификацию в отображение. Соответствующие апостериорные оценки тривиальны.
Пример: 'Display',false
Типы данных: logical
'Beta' - Значение коэффициентов регрессии для условной апостериорной оценки отклонения нарушения порядка[]) (по умолчанию) | числовой вектор-столбецЗначение коэффициентов регрессии для условной оценки апостериорного распределения отклонения нарушения порядка, заданное как разделенная разделенными запятой парами, состоящая из 'Beta' и a (PriorMdl.Intercept + PriorMdl.NumPredictors) -by-1 числовой вектор .estimate оценивает характеристики π (σ2| y, X, β = Beta), где y является y, X является X, и Beta - значение 'Beta'. Если PriorMdl.Intercept является true, затем Beta(1) соответствует точка пересечения модели. Все другие значения соответствуют переменным предиктора, которые составляют столбцы X. Beta не может содержать никаких NaN значения (то есть все коэффициенты должны быть известны).
Вы не можете задать Beta и Sigma2 одновременно.
По умолчанию, estimate не вычисляет характеристики условного апостериора σ2.
Пример: 'Beta',1:3
Типы данных: double
'Sigma2' - Значение отклонения нарушения порядка для условной апостериорной оценки коэффициентов регрессии[]) (по умолчанию) | положительный числовой скалярЗначение отклонения нарушения порядка для условной оценки апостериорного распределения коэффициентов регрессии, заданное как разделенная разделенными запятой парами, состоящая из 'Sigma2' и положительный числовой скаляр. estimate оценки характеристик π (β | y, X, Sigma2), где y является y, X является X, и Sigma2 - значение 'Sigma2'.
Вы не можете задать Sigma2 и Beta одновременно.
По умолчанию, estimate не вычисляет характеристики условного апостериора β.
Пример: 'Sigma2',1
Типы данных: double
'NumDraws' - Моделирование Монте-Карло скорректированный размер выборки1e5 (по умолчанию) | положительное целое числоСимуляция Монте-Карло скорректированный размер выборки, заданный как разделенная разделенными запятой парами, состоящая из 'NumDraws' и положительное целое число. estimate фактически рисует BurnIn – NumDraws*Thin выборки. Поэтому, estimate основывает оценки на NumDraws выборки. Для получения дополнительной информации о том, как estimate уменьшает полную выборку Монте-Карло, см. Алгоритмы.
Пример: 'NumDraws',1e7
Типы данных: double
'BurnIn' - Количество ничьих для удаления из начала выборки Монте-Карло5000 (по умолчанию) | неотрицательной скаляромКоличество розыгрышей для удаления из начала выборки Монте-Карло для уменьшения переходных эффектов, заданное как разделенная разделенными запятой парами, состоящая из 'BurnIn' и неотрицательный скаляр. Для получения дополнительной информации о том, как estimate уменьшает полную выборку Монте-Карло, см. Алгоритмы.
Совет
Чтобы помочь вам задать соответствующий размер периода горения, определите степень переходного поведения в выборке Монте-Карло, указав 'BurnIn',0, симулируя несколько тысяч наблюдений с помощью simulate, а затем графическое изображение путей.
Пример: 'BurnIn',0
Типы данных: double
'Thin' - скорректированный по Монте-Карло множитель размера выборки1 (по умолчанию) | положительное целое числоМножитель размера скорректированного Монте-Карло, заданный как разделенная разделенными запятой парами, состоящая из 'Thin' и положительное целое число.
Фактический размер выборки Монте-Карло BurnIn + NumDraws*Thin. После отбрасывания горения, estimate отбрасывает каждый Thin – 1 рисует, а затем сохраняет следующий. Для получения дополнительной информации о том, как estimate уменьшает полную выборку Монте-Карло, см. Алгоритмы.
Совет
Чтобы уменьшить потенциальную большую последовательную корреляцию в выборке Монте-Карло или уменьшить потребление памяти рисунков, сохраненных в PosteriorMdl, задайте большое значение для Thin.
Пример: 'Thin',5
Типы данных: double
'BetaStart' - Начальные значения коэффициентов регрессии для выборки MCMCНачальные значения коэффициентов регрессии для выборки Монте-Карло (MCMC) марковской цепи, заданные как разделенная разделенными запятой парами, состоящая из 'BetaStart' и числовой вектор-столбец с (PriorMdl.Intercept + PriorMdl.NumPredictors) элементы. По умолчанию BetaStart - обычная оценка методом наименьших квадратов (OLS).
Совет
Хорошей практикой является запуск estimate несколько раз с использованием различных начальных значений параметра. Проверьте, что решения из каждого запуска сходятся к аналогичным значениям.
Пример: 'BetaStart',[1; 2; 3]
Типы данных: double
'Sigma2Start' - Начальные значения отклонения нарушения порядка для выборки MCMCНачальные значения отклонения нарушения порядка для выборки MCMC, заданные как разделенная разделенными запятой парами, состоящая из 'Sigma2Start' и положительный числовой скаляр. По умолчанию Sigma2Start - остаточная средняя квадратичная невязка OLS.
Совет
Хорошей практикой является запуск estimate несколько раз с использованием различных начальных значений параметра. Проверьте, что решения из каждого запуска сходятся к аналогичным значениям.
Пример: 'Sigma2Start',4
Типы данных: double
PosteriorMdl - Байесовская линейная регрессионая модель, сохраняющая характеристики распределенияmixconjugateblm объект модели | mixsemiconjugateblm объект модели | lassoblm объект модели | empiricalblm объект моделиБайесовская линейная регрессионая модель, сохраняющая характеристики распределения, возвращенная как mixconjugateblm, mixsemiconjugateblm, lassoblm, или empiricalblm объект модели.
Если вы не задаете Beta или Sigma2 (их значения []), затем estimate обновляет предыдущую модель, используя вероятность данных, чтобы сформировать апостериорное распределение. PosteriorMdl характеризует апостериорное распределение и является empiricalblm объект модели. Информационные PosteriorMdl хранилища или отображения помогают вам решить, важны ли переменные предиктора.
Если вы задаете Beta или Sigma2, затем PosteriorMdl равен PriorMdl (две модели являются одним и тем же объектом, сохраняющим одинаковые значения свойств). estimate не обновляет предыдущую модель, чтобы сформировать апостериорную модель. Однако Summary хранит условные апостериорные оценки.
Для получения дополнительной информации об отображении PosteriorMdl, см. Summary.
Summary - Сводные данные байесовских оценокСводные данные байесовских оценок, возвращенная в виде таблицы. Summary содержит ту же информацию, что и отображение сводных данных оценок (Display). Строки соответствуют параметрам, а столбцы соответствуют этим апостериорным характеристикам:
Mean - Среднее апостериорное
Std - Апостериорное стандартное отклонение
CI95 - 95% справедливый надежный интервал
Positive - Апостериорная вероятность того, что параметр больше 0
Distribution - Описание маргинального или условного апостериорного распределения параметра, когда известно
Covariances - Оценочная ковариация матрица коэффициентов и нарушение порядка отклонения
Regime - вероятности включения переменных для моделей, которые выполняют SSVS; низкие вероятности указывают, что переменная должна быть исключена из модели
Имена строк являются именами в PriorMdl.VarNames. Имя последней строки Sigma2.
В качестве альтернативы передайте PosteriorMdl кому summarize для получения сводных данных байесовских оценок.
A Bayesian linear regression model обрабатывает параметры β и σ2 в модели многофакторной линейной регрессии (MLR) yt = xt β + εt как случайные переменные.
Для времен t = 1,..., T:
yt - наблюдаемая реакция.
xt является 1-бай- (p + 1) вектором-строкой наблюдаемых значений p предикторов. Чтобы разместить точку пересечения модели, x 1 t = 1 для всех t.
β является (p + 1) -на-1 вектор-столбец коэффициентов регрессии, соответствующих переменным, которые составляют столбцы xt.
εt является случайным нарушением порядка со средним значением нуля и Cov (ε) = σ2I T × T, в то время как ε является вектором T -by-1, содержащим все нарушения порядка. Эти предположения подразумевают, что вероятность данных является
ϕ (yt; xtβ, σ2) - Гауссова плотность вероятностей со средней xtβ и отклонением σ2 оценивается при yt;.
Прежде чем рассматривать данные, вы накладываете joint prior distribution предположение на (β, σ2). В байесовском анализе вы обновляете распределение параметров с помощью информации о параметрах, полученных из вероятности данных. Результатом является joint posterior distribution (β, σ2) или conditional posterior distributions параметров.
Симуляция Монте-Карло подвержена изменениям. Если estimate использует симуляцию Монте-Карло, тогда оценки и выводы могут варьироваться при вызове estimate несколько раз при, казалось бы, эквивалентных условиях. Чтобы воспроизвести результаты оценки, перед вызовом estimate, установите случайное число, seed при помощи rng.
Этот рисунок показывает, как estimate уменьшает выборку Монте-Карло, используя значения NumDraws, Thin, и BurnIn.
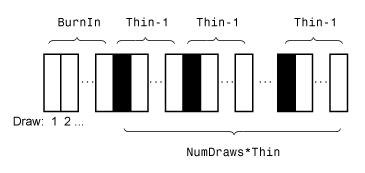
Прямоугольники представляют последовательные вытяжки из распределения. estimate удаляет белые прямоугольники из выборки Монте-Карло. Оставшиеся NumDraws чёрные прямоугольники составляют выборку Монте-Карло.
У вас есть измененная версия этого примера. Вы хотите открыть этот пример с вашими правками?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.