В этом примере показано, как использовать shorthand arima(p,D,q) синтаксис для задания MA по умолчанию
По умолчанию все параметры в созданном объекте модели имеют неизвестные значения, и инновационное распределение является Гауссовым с постоянным отклонением.
Задайте модель MA (3) по умолчанию :
Mdl = arima(0,0,3)
Mdl =
arima with properties:
Description: "ARIMA(0,0,3) Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
P: 0
D: 0
Q: 3
Constant: NaN
AR: {}
SAR: {}
MA: {NaN NaN NaN} at lags [1 2 3]
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: NaN
Этот выход показывает, что созданный объект модели, Mdl, имеет NaN значения для всех параметров модели: постоянного члена, коэффициентов MA и отклонения. Можно изменить созданный объект модели с помощью записи через точку или ввести его (вместе с данными) в estimate.
Этот пример показывает, как задать модель MA (q) с постоянным членом, равным нулю. Используйте синтаксис имя-значение, чтобы задать модель, которая отличается от модели по умолчанию .
Задайте модель MA (2) без постоянного члена ,
где инновационное распределение является Гауссовым с постоянным отклонением.
Mdl = arima('MALags',1:2,'Constant',0)
Mdl =
arima with properties:
Description: "ARIMA(0,0,2) Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
P: 0
D: 0
Q: 2
Constant: 0
AR: {}
SAR: {}
MA: {NaN NaN} at lags [1 2]
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: NaN
The MALags аргумент имя-значение задает лаги, соответствующие ненулевым коэффициентам MA. Свойство Constant в созданном объекте модели равно 0, как указано. Объект модели имеет значения по умолчанию для всех других свойств, включая NaN значения как заполнители для неизвестных параметров: коэффициенты MA и скалярное отклонение.
Можно изменить созданную переменную модели или ввести ее (вместе с данными) в estimate.
Этот пример показывает, как задать модель MA (q) с ненулевыми коэффициентами при неконсективных лагах .
Задайте модель MA (4) с ненулевыми коэффициентами MA в лагах 1 и 4 (без постоянного члена ),
где инновационное распределение является Гауссовым с постоянным отклонением.
Mdl = arima('MALags',[1,4],'Constant',0)
Mdl =
arima with properties:
Description: "ARIMA(0,0,4) Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
P: 0
D: 0
Q: 4
Constant: 0
AR: {}
SAR: {}
MA: {NaN NaN} at lags [1 4]
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: NaN
В выход показаны ненулевые коэффициенты AR в лагах 1 и 4, как задано. Свойство Q равно 4, количество предварительных примеров инноваций, необходимых для инициализации модели MA. Параметры без ограничений равны NaN.
Отобразите значение MA:
Mdl.MA
ans=1×4 cell array
{[NaN]} {[0]} {[0]} {[NaN]}
The MA массив ячеек возвращает четыре элемента. Первый и последний элементы (соответствующие лагам 1 и 4) имеют значение NaN, указывающие, что эти коэффициенты являются ненулевыми и должны быть оценены или иным образом заданы пользователем. arima устанавливает коэффициенты при промежуточных лагах равными нулю, чтобы поддерживать согласованность с индексацией массива ячеек MATLAB ® .
Этот пример показывает, как задать модель MA (q) с известными значениями параметров. Можно использовать такую полностью заданную модель в качестве входов для simulate или forecast.
Задайте модель MA (4)
где инновационное распределение является Гауссовым с постоянным отклонением 0,15.
Mdl = arima('Constant',0.1,'MA',{0.7,0.2},... 'MALags',[1,4],'Variance',0.15)
Mdl =
arima with properties:
Description: "ARIMA(0,0,4) Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
P: 0
D: 0
Q: 4
Constant: 0.1
AR: {}
SAR: {}
MA: {0.7 0.2} at lags [1 4]
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: 0.15
Все значения параметров заданы, то есть никакое свойство объекта не NaN-значен.
Этот пример показывает, как задать модель MA (q) с инновационным распределением Student's t .
Задайте модель MA (2) без постоянного члена ,
где инновационный процесс следует распределение Студента с восемью степенями свободы.
tdist = struct('Name','t','DoF',8); Mdl = arima('Constant',0,'MALags',1:2,'Distribution',tdist)
Mdl =
arima with properties:
Description: "ARIMA(0,0,2) Model (t Distribution)"
Distribution: Name = "t", DoF = 8
P: 0
D: 0
Q: 2
Constant: 0
AR: {}
SAR: {}
MA: {NaN NaN} at lags [1 2]
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: NaN
Значение Distribution является struct массив с Name полей равно 't' и полевые DoF равно 8. Когда вы задаете степени свободы, они не оцениваются, если вы вводите модель в estimate.
В приложении Econometric Modeler можно задать структуру задержки, наличие константы и инновационное распределение модели MA (q), выполнив эти шаги. Все указанные коэффициенты неизвестны, но оценочные параметры.
В командной строке откройте приложение Econometric Modeler.
econometricModeler
Также откройте приложение из галереи Apps (см. Econometric Modeler).
На панели Time Series выберите временные ряды отклика, к которому будет соответствовать модель.
На вкладке Econometric Modeler, в разделе Models, нажмите MA.
Откроется диалоговое окно MA Model Parameters.
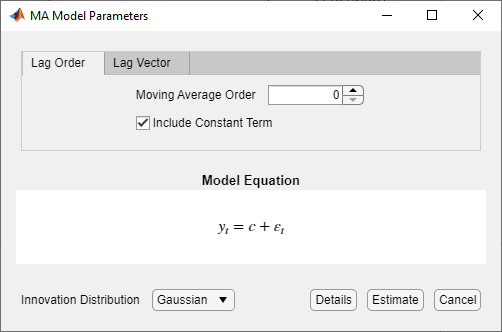
Задайте структуру задержки. Чтобы задать модель MA (q), которая включает все лаги MA с 1 по q, используйте вкладку Lag Order. Для определения гибкости включения определенных лагов используйте вкладку Lag Vector. Для получения дополнительной информации смотрите Определение полиномов оператора задержки в интерактивном режиме. Независимо от используемой вкладки, можно проверить форму модели, осмотрев уравнение в Model Equation разделе.
Для примера:
Чтобы задать модель MA (3), которая включает константу, включает первую задержку и имеет Гауссовское инновационное распределение, установите Moving Average Order на 3.
Чтобы задать модель MA (2), которая включает первую задержку, имеет Гауссово распределение, но не включает константу:
Установите Moving Average Order значение 2.
Снимите флажок Include Constant Term.
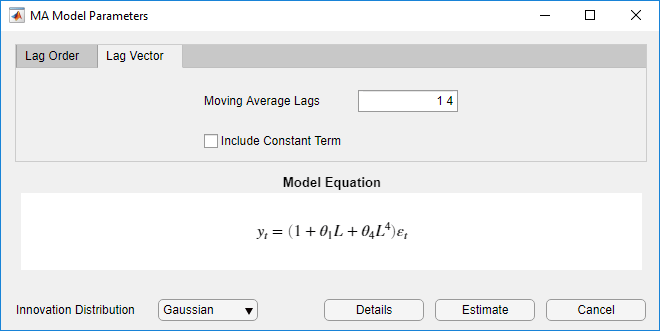
Чтобы задать модель MA (4), содержащую неконсективные лаги
где εt - серия IID Гауссовых инноваций:
Перейдите на вкладку Lag Vector.
Установите Moving Average Order значение 1 4.
Снимите флажок Include Constant Term.
Определить модель MA (2), которая включает первую задержку, включает постоянный термин и имеет t - распределенные инновации:
Установите Moving Average Lags значение 2.
Нажмите кнопку Innovation Distribution, затем выберите t.
Параметр степеней свободы t распределения является неизвестным, но оцениваемым параметром.
После того, как вы задаете модель, кликните Estimate, чтобы оценить все неизвестные параметры в модели.