Модель ARIMA (p, D, q) по умолчанию в Econometrics Toolbox™ является несезонной моделью вида
Можно записать это уравнение в конденсированной форме, используя обозначение оператора задержки:
В любом уравнении инновационное распределение по умолчанию является Гауссовым со средним нулем и постоянным отклонением.
В командной строке можно задать модель этой формы с помощью синтаксиса shorthand arima(p,D,q). Для входных параметров p, D, и q, введите количество несезонных членов AR (p), порядок несезонного интегрирования (D) и количество несезонных членов MA (q), соответственно.
Когда вы используете этот краткий синтаксис, arima создает arima модель с этими значениями свойств по умолчанию.
| Имя свойства | Тип данных свойств |
|---|---|
AR | Вектор камеры NaNs |
Beta | Пустые векторные [] коэффициентов регрессии, соответствующих экзогенным ковариатам |
Constant | NaN |
D | Степень несезонного интегрирования, D |
Distribution | "Gaussian" |
MA | Вектор камеры NaNs |
P | Количество членов AR плюс степень интегрирования, p + D |
Q | Количество членов MA, q |
SAR | Вектор камеры NaNs |
SMA | Вектор камеры NaNs |
Variance | NaN |
Чтобы назначить значения nondefault любым свойствам, можно изменить созданный объект модели с помощью записи через точку.
Заметьте, что входы D и q являются ли значения arima присваивает свойствам D и Q. Однако входной параметр p не обязательно значение arima присваивает свойству модели P. P сохраняет количество предварительных наблюдений, необходимых для инициализации AR- компонента модели. Для несезональных моделей необходимое количество предварительных наблюдений составляет p + D.
Для иллюстрации рассмотрите установку модели ARIMA (2,1,1)
где инновационный процесс является Гауссовым с (неизвестной) постоянной отклонение.
Mdl = arima(2,1,1)
Mdl =
arima with properties:
Description: "ARIMA(2,1,1) Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
P: 3
D: 1
Q: 1
Constant: NaN
AR: {NaN NaN} at lags [1 2]
SAR: {}
MA: {NaN} at lag [1]
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: NaN
Заметьте, что свойство модели P не имеет значения 2 (степень AR). При интегрировании для инициализации AR- компонента модели необходимо в общей сложности p + D (здесь 2 + 1 = 3) предварительных наблюдений.
Созданная модель, Mdl, имеет NaNs для всех параметров. A NaN сигналы значения, что параметр должен быть оценен или иным образом задан пользователем. Все параметры должны быть заданы, чтобы предсказать или симулировать модель.
Чтобы оценить параметры, введите объект модели (вместе с данными) в estimate. Это возвращает новую установленную arima объект модели. Подобранная модель имеет оценки параметров для каждого входного сигнала NaN значение.
Вызывающие arima без каких-либо входных параметров возвращает спецификацию модели ARIMA (0,0,0) со значениями свойств по умолчанию:
DefaultMdl = arima
DefaultMdl =
arima with properties:
Description: "ARIMA(0,0,0) Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
P: 0
D: 0
Q: 0
Constant: NaN
AR: {}
SAR: {}
MA: {}
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: NaN
Лучший способ задать модели для arima использует аргументы пары "имя-значение". Вам не нужно, и вы не можете задать значение для каждого свойства объекта модели. arima присваивает значения по умолчанию любым свойствам, которые вы не задаете (или не можете).
В конденсированных, запаздывающих обозначение оператора, несезонные модели ARIMA (p, D, q) имеют вид
| (1) |
Можно расширить эту модель до модели ARIMAX (p, D, q) с линейным включением экзогенных переменных. Эта модель имеет вид
| (2) |
Совет
Если вы задаете ненулевое D, затем Econometrics Toolbox различает ряд откликов, yt
до того, как предикторы войдут в модель. Вы должны предварительно обработать экзогенные ковариаты, xt путем тестирования на стационарность и дифференцирование, если таковые имеются, являются единичными корнями нестационарными. Если какой-либо нестационарный экзогенный ковариат входит в модель, то ложноотрицательная частота для тестов значимости β может увеличиться.
Для распределения нововведений, εt, существует два варианта:
Независимый и идентично распределенный (iid) Гауссов или Студенческих t с постоянным отклонением, .
Зависимый Гауссов или Студенческий t с условным процессом отклонения, . Задайте модель условного отклонения с помощью garch, egarch, или gjr модель.
The arima по умолчанию для инноваций является iid Гауссов процесс с постоянным (скалярным) отклонением.
В порядок оценки, прогноза или симуляции модели необходимо задать параметрическую форму модели (например, которая отстает от ненулевых коэффициентов, инновационного распределения) и любых известных значений параметров. Можно задать любые неизвестные параметры равными NaN, и затем введите модель, чтобы estimate (вместе с данными), чтобы получить оцененные значения параметров.
arima (и estimate) возвращает модель, соответствующую спецификации модели. Можно изменять модели, чтобы изменить или обновить спецификацию. Входные модели (без NaN значения) к forecast или simulate для прогнозирования и симуляции, соответственно. Вот некоторые примеры спецификаций, использующих аргументы имя-значение.
| Модель | Спецификация |
|---|---|
| arima('AR',NaN) или arima(1,0,0) |
| arima ('Constant', 0, 'MA', {NaN, NaN},... |
| arima ('Constant', 0,2, 'AR', 0,8, 'MA', 0,6, 'D', 1,... |
|
| arima('Constant',0,'AR',-0.5,'D',1,'Beta',[-5 2]) |
Можно задать следующие аргументы имя-значение, чтобы создать несезонные arima модели.
Аргументы имя-значение для несезонных моделей ARIMA
| Имя | Соответствующий термин (ы) модели в уравнении 1 | Когда задавать |
|---|---|---|
AR | Несезонные коэффициенты AR, | Чтобы задать ограничения равенства для коэффициентов AR. Для примера задать коэффициенты AR в модели задайте Вам нужно задать только ненулевые элементы Любые заданные вами коэффициенты должны соответствовать стабильному AR оператора полиному. |
ARLags | Лаги, соответствующие ненулевым, несезонным коэффициентам AR |
Используйте этот аргумент как ярлык для определения Использование |
Beta | Значения коэффициентов экзогенных ковариат | Используйте этот аргумент, чтобы задать значения коэффициентов экзогенных переменных. Для примера используйте По умолчанию |
Constant | Константа, c | Чтобы задать ограничения равенства для c. Для примера, для модели без постоянного члена, задайте 'Constant',0.По умолчанию Constant имеет значение NaN. |
D | Степень несезонного дифференцирования, D | Чтобы задать степень несезонного дифференцирования, больше нуля. Для примера, чтобы задать одну степень дифференцирования, задайте 'D',1.По умолчанию D имеет значение 0 (что означает отсутствие несезонного интегрирования). |
Distribution | Распределение инновационного процесса | Используйте этот аргумент, чтобы задать t инновационное распределение Student. По умолчанию инновационное распределение является Гауссовым. Для примера, чтобы задать распределение t с неизвестными степенями свободы, задайте 'Distribution','t'.Чтобы задать t инновационное распределение с известными степенями свободы, присвойте Distribution структуру данных с полями Name и DoF. Для примера для распределения t с девятью степенями свободы задайте 'Distribution',struct('Name','t','DoF',9). |
MA | Несезонные коэффициенты MA, | Чтобы задать ограничения равенства для коэффициентов MA. Для примера задать коэффициенты MA в модели задайте Вам нужно задать только ненулевые элементы Любые заданные коэффициенты должны соответствовать инвертируемому полиному MA. |
MALags | Лаги, соответствующие ненулевым, несезонным коэффициентам MA |
Используйте этот аргумент как ярлык для определения задайте Использование |
Variance |
|
|
Примечание
Вы не можете назначить значения свойствам P и Q. Для несезонных моделей,
arima устанавливает P равно p + D
arima устанавливает Q равно q
Для временных рядов с s периодичности задайте степень ps сезонный полином AR оператора, , и степень qs сезонного оператора MA, полинома . Точно так же задайте степень p несезонный полином оператора AR, , и степень q несезонного полинома оператора MA,
| (3) |
Мультипликативная модель ARIMA со степенью D несезонным интегрированием и степенью s сезонности задается
| (4) |
arima по умолчанию для инновационного распределения является iid Гауссов процесс с постоянным (скалярным) отклонением.В дополнение к аргументам для определения несезонных моделей (описанным в Аргументах Имя-Значение для Несезонных Моделей ARIMA), можно задать эти аргументы имя-значение, чтобы создать мультипликативное arima модель. Можно расширить модель ARIMAX аналогично, чтобы включить сезонные эффекты.
Аргументы имя-значение для сезонных моделей ARIMA
| Аргумент | Соответствующий термин (ы) модели в уравнении 4 | Когда задавать |
|---|---|---|
SAR | Сезонные коэффициенты AR, | Чтобы задать ограничения равенства для сезонных коэффициентов AR. При задании коэффициентов AR используйте знак, противоположный тому, что появляется в Уравнении 4 (то есть используйте знак коэффициента так, как он появился бы в правой части уравнения). Использование Для примера, чтобы задать модель задайте Любые значения коэффициентов, которые вы вводите, должны соответствовать стабильной сезонной AR- полинома. |
SARLags | Лаги, соответствующие ненулевым сезонным коэффициентам AR, в периодичности наблюдаемого ряда |
Используйте этот аргумент при указании Для примера, чтобы задать модель задайте |
SMA | Сезонные коэффициенты MA, | Чтобы задать ограничения равенства для сезонных коэффициентов MA. Использование Для примера, чтобы задать модель задайте Любые значения коэффициентов, которые вы вводите, должны соответствовать инвертируемому сезонному полиному MA. |
SMALags | Лаги, соответствующие ненулевым сезонным коэффициентам MA, в периодичности наблюдаемого ряда |
Используйте этот аргумент при указании Для примера, чтобы задать модель задайте |
Seasonality | Сезонная периодичность, s | Чтобы задать степень сезонного интегрирования s в сезонном дифференцированном полиноме Δs = 1 - Ls. Например, чтобы определить периодичность для сезонного интегрирования ежемесячных данных, укажите 'Seasonality',12.Если вы задаете ненулевое Seasonality, тогда степень всего сезонного дифференцирования полинома едина. По умолчанию Seasonality имеет значение 0 (что означает периодичность и отсутствие сезонного интегрирования). |
Примечание
Вы не можете назначить значения свойствам P и Q. Для мультипликативных моделей ARIMA,
arima устанавливает P равно p + D + ps + s
arima устанавливает Q равно q + qs
Вы можете задать структуру задержки и распределение инноваций сезонных и несезонных условных средних моделей, используя Econometric Modeler приложение. Приложение рассматривает все коэффициенты как неизвестные и оценочные, включая параметр степеней свободы для t инновационного распределения.
В командной строке откройте приложение Econometric Modeler.
econometricModeler
Также откройте приложение из галереи Apps (см. Econometric Modeler).
В приложении можно увидеть все поддерживаемые модели, выбрав переменную временных рядов для ответа на панели Time Series. Затем на вкладке Econometric Modeler, в разделе Models, щелкните стреле, чтобы отобразить галерею моделей.
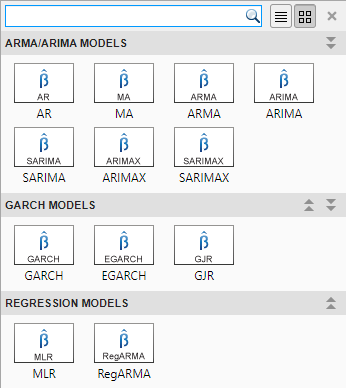
Раздел ARMA/ARIMA Models содержит поддерживаемые условные средние модели.
Для оценки условной средней модели SARIMA и SARIMAX являются наиболее гибкими моделями. Можно создать любую условную среднюю модель, которая исключает экзогенные предикторы, нажав SARIMA, или можно создать любую условную среднюю модель, которая включает, по крайней мере, один экзогенный предиктор, нажав SARIMAX.
После выбора модели приложение отображает Type Диалоговое окно «Параметры модели», где Type является типом модели. Этот рисунок показывает диалоговое окно SARIMAX Model Parameters.
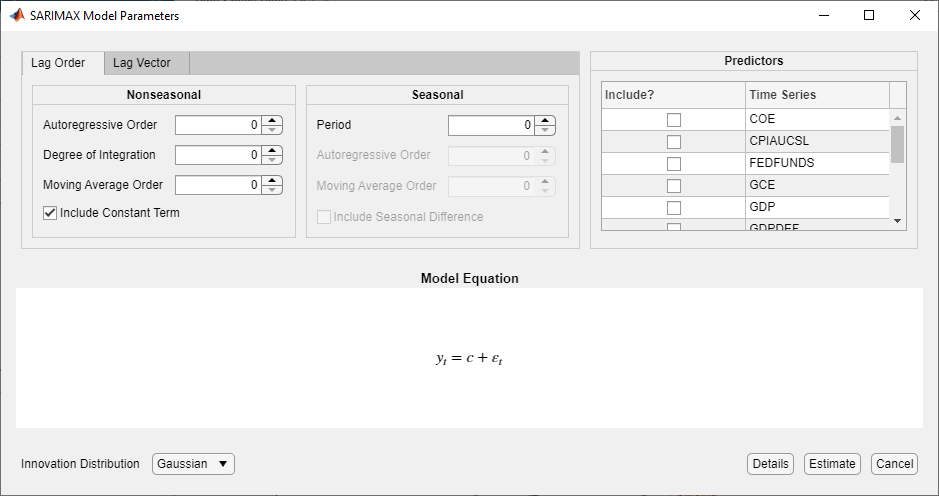
Настраиваемые параметры в диалоговом окне зависят от Type. В целом регулируемые параметры включают:
Константа модели и линейные коэффициенты регрессии, соответствующая переменным предиктора
Параметры компонента временных рядов, которые включают сезонные и несезонные лаги и степени интегрирования
Инновационное распределение
Когда вы корректируете значения параметров, уравнение в Model Equation разделе изменяется так, чтобы оно совпадало с вашими спецификациями. Регулируемые параметры соответствуют входу и аргументам пары "имя-значение", описанным в предыдущих разделах и в arima страница с описанием.
Для получения дополнительной информации об указании моделей с помощью приложения, смотрите Подбор моделей к данным и Определение полиномов оператора задержки в интерактивном режиме.