Документация

Что такое стохастический процесс?

_yt временных рядов является набором наблюдений за переменной, индексируемой последовательно в течение нескольких временных точек t = 1, 2,..., T. Наблюдения временных рядов _y 1, y 2,.._., yT по своей сути зависимы. С точки зрения статистического моделирования это означает, что нецелесообразно рассматривать временные ряды как случайную выборку независимых наблюдений.

Цель статистического моделирования состоит в том, чтобы найти компактное представление процесса генерации данных для ваших данных. Статистический базовый блок эконометрического моделирования временных рядов является стохастическим процессом. Эвристически stochastic process является распределением вероятностей соединений для набора случайных переменных. Путем моделирования наблюдаемых временных рядов _yt как реализация из стохастического процесса $$y=\left\{y_t;t=1,\mathrm{...},T\right\}$$возможно учесть высокомерный и зависимый характер данных. Набор T времени наблюдения может быть дискретным или непрерывным. Рисунок 1-1, Monthly Average CO2 отображает среднюю месячную концентрацию _CO2 (ppm), зарегистрированную обсерваторией Мауна-Лоа на Гавайях с 1980 по 2012 год [3].

Стационарные процессы

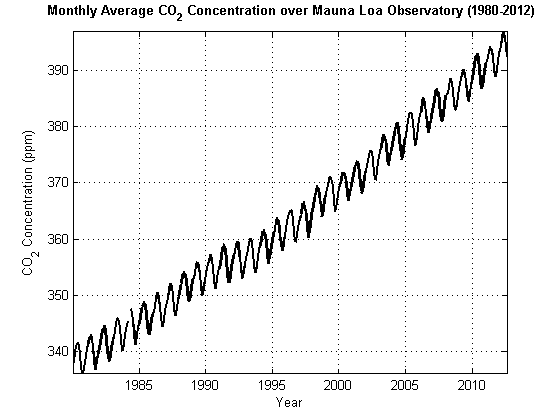
Стохастические процессы являются weakly stationary или covariance stationary (или просто, stationary), если их первые два момента являются конечными и постоянными с течением времени. В частности, если _yt является стационарным стохастическим процессом, то для всех t:

График вашего стохастического процесса, кажется, увеличивается или уменьшается без привязки? Ответ на этот вопрос указывает, является ли стохастический процесс стационарным. «Да» указывает, что стохастический процесс может быть нестационарным. На фигура, Monthly Average CO2, концентрация _CO2 увеличивается без привязки, что указывает на нестационарный стохастический процесс.

Модель линейных временных рядов

Теорема Уолда [2] утверждает, что можно записать все слабо стационарные стохастические процессы в общей линейной форме

Вот, $${\epsilon }_t$$ обозначает последовательность некоррелированных (но не обязательно независимых) случайных переменных из четко определенного распределения вероятностей со средним нулем. Его часто называют innovation process, потому что он захватывает всю новую информацию в системе в t времени.

Процесс корня модуля

Линейная модель временного ряда является unit root process, если набор решений его характеристического уравнения содержит корень, который находится на модуль круге (то есть имеет абсолютное значение единицы). Впоследствии ожидаемое значение, отклонение или ковариация элементов стохастического процесса растет со временем, и поэтому является нестационарной. Если у вашей серии есть модуль корень, то дифференцирование может сделать ее стационарной.

Для примера рассмотрим линейную модель временных рядов $$y_t=y_{t-1}+{\epsilon }_t,$$ где $${\epsilon }_t$$ - белая шумовая последовательность инноваций с отклонением² (это называется случайной прогулкой). Характеристическое уравнение этой модели $$z-1=0,$$ который имеет корень единицы. Если начальная _y0 наблюдения фиксирована, то можно записать модель как $$y_t=y_0+{\displaystyle \sum _{i=1}^t{\epsilon }_i}.$$ Его ожидаемое значение _y0, что не зависит от времени. Однако отклонение ряда является t,², который растет со временем, делая серию нестабильной. Возьмите первое различие, чтобы преобразовать ряд, и модель станет $$d_t=y_t-y_{t-1}={\epsilon }_t$$. Характеристическое уравнение для этого ряда $$z=0$$так что у него нет корня модуля. Обратите внимание, что

Рисунок 1-1, Monthly Average CO2 выглядит нестационарным. Что произойдет, если построить первое различие _dt = _{yt – y  t} -1 этой серии? Рисунок 1-2, Ежемесячное различие в CO2 отображает dt. Игнорируя колебания, стохастический процесс, по-видимому, не увеличивается или уменьшается в целом. Можно сделать вывод, что dt является стационарным, и что yt является единичным корнем нестационарным. Для получения дополнительной информации смотрите Дифференцирование.

Обозначение оператора задержки

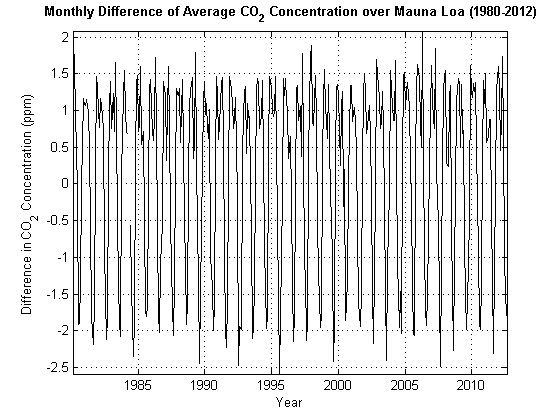
lag operator L работает с временными рядами yt такими что $$L^i{y}_t=y_{t-i}$$.

Полином m-градусной задержки коэффициентов _b 1, b 2,.._., bm задан как

В обозначении оператора задержки можно записать общую линейную модель с помощью полинома бесконечной степени $$\psi (L)=(1+{\psi }_{1}L+{\psi }_2{L}^2+\dots ),$$

Вы не можете оценить модель, которая имеет полином бесконечной степени коэффициентов с конечным количеством данных. Однако, если $$\psi (L)$$ является рациональным полиномом (или приблизительно рациональным), можно записать его (по крайней мере, приблизительно) как частный из двух полиномов конечной степени.

Задайте q степень $$\theta (L)=(1+{\theta }_{1}L+{\theta }_2{L}^2+\dots +{\theta }_q{L}^q)$$ и p степень $$\varphi (L)=(1+{\varphi }_{1}L+{\varphi }_2{L}^2+\dots +{\varphi }_p{L}^p)$$. Если $$\psi (L)$$ рационально, тогда

Таким образом, по теореме Уолда можно смоделировать (или близко аппроксимировать) каждый стационарный стохастический процесс как

который имеет p + q коэффициентов (конечное число).

Характеристическое уравнение

Степень p characteristic polynomial модели линейных временных рядов $$y_t={\varphi }_1{y}_{t-1}+{\varphi }_2{y}_{t-2}+\mathrm{...}+{\varphi }_p{y}_{t-p}+{\epsilon }_t$$ является

Это другой способ оценить, что серия является стационарным процессом. Для примера, характеристическое уравнение $$y_t=0.5y_{t-1}-0.02y_{t-2}+{\epsilon }_t$$ является $$\varphi (a)=a^2-0.5a+\mathrm{0.02.}$$

Корни homogeneous characteristic equation $$\varphi (a)=0$$ (называемый characteristic roots) определить, являются ли линейные временные ряды стационарным. Если каждый корень в $$\varphi (a)$$ лежит внутри модуля круга, затем процесс стационарный. Корни лежат внутри единичной окружности, если абсолютное значение меньше единицы. Это - модуль корневой процесс, если один или несколько корней лежат внутри модуля круга (т.е. имеют абсолютное значение единицы). Продолжая пример, характерные корни $$\varphi (a)=0$$ являются $$a=\{0.4562,0.0438\}.$$ Поскольку абсолютные значения этих корней меньше единицы, линейная модель временных рядов является стационарной.