Задайте модели GJR

Модель GJR по умолчанию

Модель GJR (P, Q) по умолчанию в Econometrics Toolbox™ имеет вид

$ε_{t} = σ_{t} z_{t},$

с Гауссовым инновационным распределением и

$σ_{t}^{2} = κ + \sum_{i = 1}^{P} γ_{i} σ_{t - i}^{2} + \sum_{j = 1}^{Q} α_{j} ε_{t - j}^{2} + \sum_{j = 1}^{Q} ξ_{j} I [ε_{t - j} < 0] ε_{t - j}^{2} .$

Функция индикации $I [ε_{t - j} < 0]$ равен 1, если $ε_{t - j} < 0$ и 0 в противном случае. Модель по умолчанию не имеет среднего смещения, и отстающие отклонения и квадратные нововведения находятся при последовательных лагах.

Можно задать модель этой формы с помощью синтаксиса shorthand gjr(P,Q). Для входных параметров P и Q, введите количество отстающих отклонений (условия GARCH), P и отстающих квадратов инноваций (ARCH и условия использования), Q, соответственно. Действуют следующие ограничения:

P и Q должны быть неотрицательными целыми числами.
Если P > 0, то вы также должны задать Q > 0

Когда вы используете этот краткий синтаксис, gjr создает gjr модель с этими значениями свойств по умолчанию.

Свойство	Значение по умолчанию
`P`	Количество членов GARCH, P
`Q`	Количество ARCH и условия использования, Q
`Offset`	`0`
`Constant`	`NaN`
`GARCH`	Вектор камеры `NaN`s
`ARCH`	Вектор камеры `NaN`s
`Leverage`	Вектор камеры `NaN`s
`Distribution`	`"Gaussian"`

Чтобы назначить значения nondefault любым свойствам, можно изменить созданную модель с помощью записи через точку.

Для иллюстрации рассмотрите определение модели GJR (1,1)

$ε_{t} = σ_{t} z_{t},$

с Гауссовым инновационным распределением и

$σ_{t}^{2} = κ + γ_{1} σ_{t - 1}^{2} + α_{1} ε_{t - 1}^{2} + ξ_{1} I [ε_{t - 1} < 0] ε_{t - 1}^{2} .$

Mdl = gjr(1,1)

Mdl = 
  gjr with properties:

     Description: "GJR(1,1) Conditional Variance Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: 0

Созданная модель, Mdl, имеет NaNs для всех параметров модели. A NaN сигналы значения, что параметр должен быть оценен или иным образом задан пользователем. Все параметры должны быть заданы, чтобы предсказать или симулировать модель.

Чтобы оценить параметры, введите модель (вместе с данными), чтобы estimate. Это возвращает новую установленную gjr модель. Подобранная модель имеет оценки параметров для каждого входного NaN значение.

Вызывающие gjr без каких-либо входных параметров возвращает спецификацию модели GJR (0,0) со значениями свойств по умолчанию:

DefaultMdl = gjr

DefaultMdl = 
  gjr with properties:

     Description: "GJR(0,0) Conditional Variance Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 0
               Q: 0
        Constant: NaN
           GARCH: {}
            ARCH: {}
        Leverage: {}
          Offset: 0

Задайте модель GJR по умолчанию

Открыть Live Script

В этом примере показано, как использовать shorthand gjr(P,Q) синтаксис для определения модели GJR (P, Q) по умолчанию , $ε_{t} = σ_{t} z_{t}$ с Гауссовым инновационным распределением и

$σ_{t}^{2} = κ + \sum_{i = 1}^{P} γ_{i} σ_{t - i}^{2} + \sum_{j = 1}^{Q} α_{j} ε_{t - j}^{2} + \sum_{j = 1}^{Q} ξ_{j} I [ε_{t - j} < 0] ε_{t - j}^{2} .$

По умолчанию все параметры в созданной модели имеют неизвестные значения.

Задайте модель GJR (1,1) по умолчанию :

Mdl = gjr(1,1)

Mdl = 
  gjr with properties:

     Description: "GJR(1,1) Conditional Variance Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: 0

Выход показывает, что созданная модель Mdl, имеет NaN значения для всех параметров модели: постоянный член, коэффициент GARCH, коэффициент ARCH и коэффициент рычага. Можно изменить созданную модель с помощью записи через точку или ввести ее (вместе с данными) в estimate.

Использование аргументов в виде пар имя-значение

Самый гибкий способ задать модели GJR - это использовать аргументы пары "имя-значение". Вам не нужно, и вы не можете задать значение для каждого свойства модели. gjr присваивает значения по умолчанию любым свойствам модели, которые вы не задаете (или не можете).

Общая модель GJR (P, Q) имеет вид

$y_{t} = μ + ε_{t},$

где $ε_{t} = σ_{t} z_{t}$ и

$σ_{t}^{2} = κ + \sum_{i = 1}^{P} γ_{i} σ_{t - i}^{2} + \sum_{j = 1}^{Q} α_{j} ε_{t - j}^{2} + \sum_{j = 1}^{Q} ξ_{j} I [ε_{t - j} < 0] ε_{t - j}^{2} .$

Инновационное распределение может быть Гауссовым или Студенческим t. Распределением по умолчанию является Гауссов.

В порядок оценки, прогноза или симуляции модели необходимо задать параметрическую форму модели (например, которая отстает от ненулевых коэффициентов, инновационного распределения) и любых известных значений параметров. Можно задать любые неизвестные параметры равными NaN, и затем введите модель, чтобы estimate (вместе с данными), чтобы получить оцененные значения параметров.

gjr (и estimate) возвращает модель, соответствующую спецификации модели. Можно изменять модели, чтобы изменить или обновить спецификацию. Входные модели (без NaN значения) к forecast или simulate для прогнозирования и симуляции, соответственно. Вот некоторые примеры спецификаций, использующих аргументы имя-значение.

Модель	Спецификация
$y_{t} = ε_{t}$ $ε_{t} = σ_{t} z_{t}$ _zt Гауссов $σ_{t}^{2} = κ + γ_{1} σ_{t - 1}^{2} + α_{1} ε_{t - 1}^{2} + ξ_{1} I [ε_{t - 1} < 0] ε_{t - 1}^{2}$	`gjr ('GARCH', NaN, 'ARCH', NaN,... 'Leverage', NaN)` или `gjr(1,1)`
$y_{t} = μ + ε_{t}$ $ε_{t} = σ_{t} z_{t}$ _zt t студента с неизвестными степенями свободы $σ_{t}^{2} = κ + γ_{1} σ_{t - 1}^{2} + α_{1} ε_{t - 1}^{2} + ξ_{1} I [ε_{t - 1} < 0] ε_{t - 1}^{2}$	`gjr ('Offset', NaN, 'GARCH', NaN,... 'ARCH', NaN, 'Leverage', NaN,... 'Distribution', 't')`
$y_{t} = ε_{t}$ $ε_{t} = σ_{t} z_{t}$ _zt t студента с восемью степенями свободы $σ_{t}^{2} = 0.1 + 0.6 σ_{t - 1}^{2} + 0.3 ε_{t - 1}^{2} + 0.05 I [ε_{t - 1} < 0] ε_{t - 1}^{2}$	`gjr ('Constant', 0,1, 'GARCH', 0,6,... 'ARCH', 0,3, 'Leverage', 0,05,... 'Распределение'... struct ('Name', 't', 'DoF', 8)`

Вот полное описание аргументов имя-значение, которые можно использовать для задания моделей GJR.

Примечание

Вы не можете назначить значения свойствам P и Q. egarch устанавливает P равен наибольшей задержке GARCH, и Q равен наибольшей задержке с ненулевым квадратным коэффициентом инновации, включая ARCH и коэффициенты рычага.

Аргументы имя-значение для моделей GJR

Имя	Соответствующий термин (ы) модели GJR	Когда задавать
`Offset`	Среднее смещение, μ	Включение ненулевого среднего смещения. Для примера, `'Offset',0.2`. Если вы планируете оценить срок смещения, задайте `'Offset',NaN`. По умолчанию `Offset` имеет значение `0` (то есть без смещения).
`Constant`	Константа в модели условного отклонения, κ	Чтобы задать ограничения равенства для κ. Для примера, если модель имеет известную константу 0,1, задайте `'Constant',0.1`. По умолчанию `Constant` имеет значение `NaN`.
`GARCH`	Коэффициенты GARCH, $γ_{1}, \dots, γ_{P}$	Чтобы задать ограничения равенства для коэффициентов GARCH. Для примера задать модель GJR (1,1) с $γ_{1} = 0.6,$ задайте `'GARCH',0.6`. Вам нужно задать только ненулевые элементы `GARCH`. Если ненулевые коэффициенты находятся в неконсективных лагах, задайте соответствующие лаги, используя `GARCHLags`. Все заданные коэффициенты должны удовлетворять всем ограничениям стационарности.
`GARCHLags`	Лаги, соответствующие ненулевым коэффициентам GARCH	`GARCHLags` не является свойством модели. Используйте этот аргумент как ярлык для определения `GARCH` когда ненулевые коэффициенты GARCH соответствуют неконсективным лагам. Для примера задать ненулевые коэффициенты GARCH в лагах 1 и 3, например, ненулевые $γ_{1}$ и $γ_{3},$ задайте `'GARCHLags',[1,3]`. Использование `GARCH` и `GARCHLags` вместе для задания известных ненулевых коэффициентов GARCH при неконсективных лагах. Для примера, если $γ_{1} = 0.3$ и $γ_{3} = 0.1,$ задайте `'GARCH',{0.3,0.1},'GARCHLags',[1,3]`
`ARCH`	Коэффициенты ARCH, $α_{1}, \dots, α_{Q}$	Чтобы задать ограничения равенства для коэффициентов ARCH. Для примера задать модель GJR (1,1) с $α_{1} = 0.3,$ задайте `'ARCH',0.3`. Вам нужно задать только ненулевые элементы `ARCH`. Если ненулевые коэффициенты находятся в неконсективных лагах, задайте соответствующие лаги, используя `ARCHLags`.
`ARCHLags`	Лаги, соответствующие ненулевым коэффициентам ARCH	`ARCHLags` не является свойством модели. Используйте этот аргумент как ярлык для определения `ARCH` когда ненулевые коэффициенты ARCH соответствуют неконсективным лагам. Для примера задать ненулевые коэффициенты ARCH в лагах 1 и 3, например, ненулевые $α_{1}$ и $α_{3},$ задайте `'ARCHLags',[1,3]`. Использование `ARCH` и `ARCHLags` вместе для задания известных ненулевых коэффициентов ARCH при неконсективных лагах. Для примера, если $α_{1} = 0.4$ и $α_{3} = 0.2,$ задайте `'ARCH',{0.4,0.2},'ARCHLags',[1,3]`
`Leverage`	Коэффициенты использования, $ξ_{1}, \dots, ξ_{Q}$	Чтобы задать ограничения равенства для коэффициентов плеча. Для примера задать модель GJR (1,1) с $ξ_{1} = 0.1$ задайте `'Leverage',0.1`. Вам нужно задать только ненулевые элементы `Leverage`. Если ненулевые коэффициенты находятся в неконсективных лагах, задайте соответствующие лаги, используя `LeverageLags`.
`LeverageLags`	Лаги, соответствующие ненулевым коэффициентам использования	`LeverageLags` не является свойством модели. Используйте этот аргумент как ярлык для определения `Leverage` когда ненулевые коэффициенты рычага соответствуют неконсективным лагам. Для примера задать ненулевые коэффициенты использования в лагах 1 и 3, например, ненулевые $ξ_{1}$ и $ξ_{3},$ задайте `'LeverageLags',[1,3]`. Использование `Leverage` и `LeverageLags` вместе, чтобы задать известные ненулевые коэффициенты рычага при неконсективных лагах. Для примера, если $ξ_{1} = 0.1$ и $ξ_{3} = 0.05,$ задайте `'Leverage',{0.1,0.05},'LeverageLags',[1,3]`.
`Distribution`	Распределение инновационного процесса	Используйте этот аргумент, чтобы задать t инновационное распределение Student. По умолчанию инновационное распределение является Гауссовым. Для примера, чтобы задать распределение t с неизвестными степенями свободы, задайте `'Distribution','t'`. Чтобы задать t инновационное распределение с известными степенями свободы, присвойте `Distribution` структуру данных с полями `Name` и `DoF`. Для примера для распределения t с девятью степенями свободы задайте `'Distribution',struct('Name','t','DoF',9)`.

Задайте модель GJR используя приложение Econometric Modeler

Вы можете задать структуру задержки, распределение инноваций и рычаги моделей GJR, используя Econometric Modeler приложение. Приложение рассматривает все коэффициенты как неизвестные и оценочные, включая параметр степеней свободы для t инновационного распределения.

В командной строке откройте приложение Econometric Modeler.

econometricModeler

Также откройте приложение из галереи Apps (см. Econometric Modeler).

В приложении можно увидеть все поддерживаемые модели, выбрав переменную временных рядов для ответа на панели Time Series. Затем на вкладке Econometric Modeler, в разделе Models, щелкните стреле, чтобы отобразить галерею моделей.

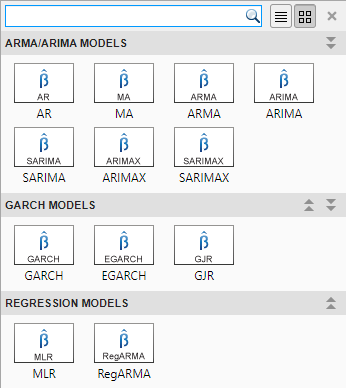
Раздел GARCH Models содержит все поддерживаемые модели условных отклонений. Чтобы задать модель GJR, нажмите GJR. Откроется диалоговое окно GJR Model Parameters.

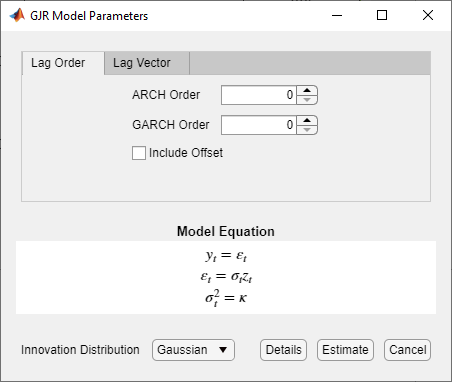
Настраиваемые параметры включают:

GARCH Degree - Порядок полинома GARCH.
ARCH Degree - Порядок полинома ARCH. Значение этого параметра также задает порядок полинома рычага.
Include Offset - включение смещения модели.
Innovation Distribution - Инновационное распределение.

Когда вы корректируете значения параметров, уравнение в Model Equation разделе изменяется так, чтобы оно совпадало с вашими спецификациями. Регулируемые параметры соответствуют входу и аргументам пары "имя-значение", описанным в предыдущих разделах и в gjr страница с описанием.

Для получения дополнительной информации об указании моделей с помощью приложения, смотрите Подбор моделей к данным и Определение полиномов оператора задержки в интерактивном режиме.

Задайте модель GJR со средним смещением

Открыть Live Script

В этом примере показано, как задать модель GJR (P, Q) со средним смещением. Используйте аргументы пары "имя-значение", чтобы задать модель, которая отличается от модели по умолчанию .

Задайте модель GJR (1,1) со средним смещением ,

$y_{t} = μ + ε_{t},$

где $ε_{t} = σ_{t} z_{t}$ и

$σ_{t}^{2} = κ + γ_{1} σ_{t - 1}^{2} + α_{1} ε_{t - 1}^{2} + ξ_{1} I [ε_{t - 1} < 0] ε_{t - 1}^{2} .$

Mdl = gjr('Offset',NaN,'GARCHLags',1,'ARCHLags',1,...
    'LeverageLags',1)

Mdl = 
  gjr with properties:

     Description: "GJR(1,1) Conditional Variance Model with Offset (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: NaN

Среднее смещение появляется в выходе как дополнительный параметр, который будет оценен или иначе задан.

Задайте модель GJR с неконсективными лагами

Открыть Live Script

Этот пример показывает, как задать модель GJR с ненулевыми коэффициентами при неконсективных лагах.

Задайте модель GJR (3,1) с ненулевыми терминами GARCH при лагах 1 и 3. Включите среднее смещение .

Mdl = gjr('Offset',NaN,'GARCHLags',[1,3],'ARCHLags',1,...
    'LeverageLags',1)

Mdl = 
  gjr with properties:

     Description: "GJR(3,1) Conditional Variance Model with Offset (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 3
               Q: 1
        Constant: NaN
           GARCH: {NaN NaN} at lags [1 3]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: NaN

Неизвестные ненулевые коэффициенты GARCH соответствуют отстающим отклонениям при лагах 1 и 3. Выходные выходы показывают только ненулевые коэффициенты.

Отобразите значение GARCH:

Mdl.GARCH

ans=1×3 cell array
    {[NaN]}    {[0]}    {[NaN]}

The GARCH массив ячеек возвращает три элемента. Первый и третий элементы имеют значение NaN, указывающие, что эти коэффициенты ненулевые и должны быть оценены или указаны иным образом. По умолчанию gjr устанавливает промежуточный коэффициент при задержке 2 равной нулю, чтобы поддерживать согласованность с индексацией массива ячеек MATLAB ® .

Задайте модель GJR с известными значениями параметров

Открыть Live Script

Этот пример показывает, как задать модель GJR с известными значениями параметров. Можно использовать такую полностью заданную модель в качестве входов для simulate или forecast.

Задайте модель GJR (1,1)

$σ_{t}^{2} = 0.1 + 0.6 σ_{t - 1}^{2} + 0.2 ε_{t - 1}^{2} + 0.1 I [ε_{t - 1} < 0] ε_{t - 1}^{2}$

с Гауссовым инновационным распределением.

Mdl = gjr('Constant',0.1,'GARCH',0.6,'ARCH',0.2,...
    'Leverage',0.1)

Mdl = 
  gjr with properties:

     Description: "GJR(1,1) Conditional Variance Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: 0.1
           GARCH: {0.6} at lag [1]
            ARCH: {0.2} at lag [1]
        Leverage: {0.1} at lag [1]
          Offset: 0

Поскольку все значения параметров заданы, созданная модель не имеет NaN значения. Функции simulate и forecast не принимайте входные модели с NaN значения.

Задайте модель GJR с t инновационными Распределениями

Открыть Live Script

В этом примере показано, как задать модель GJR с инновационным распределением Student's t.

Задайте модель GJR (1,1) со средним смещением ,

$y_{t} = μ + ε_{t},$

где $ε_{t} = σ_{t} z_{t}$ и

$σ_{t}^{2} = κ + γ_{1} σ_{t - 1}^{2} + α_{1} ε_{t - 1}^{2} + ξ_{1} I [ε_{t - 1} < 0] ε_{t - 1}^{2} .$

Принять $z_{t}$ следует инновационному распределению Студента с 10 степенями свободы.

tDist = struct('Name','t','DoF',10);
Mdl = gjr('Offset',NaN,'GARCHLags',1,'ARCHLags',1,...
              'LeverageLags',1,'Distribution',tDist)

Mdl = 
  gjr with properties:

     Description: "GJR(1,1) Conditional Variance Model with Offset (t Distribution)"
    Distribution: Name = "t", DoF = 10
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: NaN

Значение Distribution является struct массив с Name полей равно 't' и полевые DoF равно 10. Когда вы задаете степени свободы, они не оцениваются, если вы вводите модель в estimate.

Документация