Симуляция Монте-Карло коррелированных возвратов активов
RetSeries = portsim(ExpReturn,ExpCovariance,NumObs)NASSETS активы по NUMOBS последовательные интервалы наблюдений. Возвраты активов моделируются как пропорциональные шаги постоянного дрейфа, стохастические процессы постоянной волатильности, тем самым аппроксимируя геометрическое броуновское движение в непрерывном времени.
RetSeries = portsim(___,RetIntervals,NumSim,Method)
Этот пример показывает различие между Exact и Expected методы симуляции.
Рассмотрим портфель из пяти активов со следующей ожидаемыми возвратами, стандартными отклонениями и корреляционной матрицей на основе ежедневных возвратов активов (где ExpReturn и Sigmas делятся на 100, чтобы преобразовать проценты в возвраты).
ExpReturn = [0.0246 0.0189 0.0273 0.0141 0.0311]/100;
Sigmas = [0.9509 1.4259 1.5227 1.1062 1.0877]/100;
Correlations = [1.0000 0.4403 0.4735 0.4334 0.6855
0.4403 1.0000 0.7597 0.7809 0.4343
0.4735 0.7597 1.0000 0.6978 0.4926
0.4334 0.7809 0.6978 1.0000 0.4289
0.6855 0.4343 0.4926 0.4289 1.0000];Преобразуйте корреляции и стандартные отклонения в матрицу ковариации.
ExpCovariance = corr2cov(Sigmas, Correlations)
ExpCovariance = 5×5
10-3 ×
0.0904 0.0597 0.0686 0.0456 0.0709
0.0597 0.2033 0.1649 0.1232 0.0674
0.0686 0.1649 0.2319 0.1175 0.0816
0.0456 0.1232 0.1175 0.1224 0.0516
0.0709 0.0674 0.0816 0.0516 0.1183
Предположим, что в календарном году существует 252 торговых дня, и моделируйте два пути расчета (реализации) суточных возвратов в течение двухлетнего периода. Начиная с ExpReturn и ExpCovariance выражаются ежедневно, задаются RetIntervals = 1.
StartPrice = 100; NumObs = 504; % two calendar years of daily returns NumSim = 2; RetIntervals = 1; % one trading day NumAssets = 5;
Чтобы проиллюстрировать различие между методами, моделируйте два пути каждым методом, начиная с одного и того же состояния случайных чисел.
rng('default'); RetExact = portsim(ExpReturn, ExpCovariance, NumObs, ... RetIntervals, NumSim, 'Exact'); rng(0); RetExpected = portsim(ExpReturn, ExpCovariance, NumObs, ... RetIntervals, NumSim, 'Expected');
Сравните среднее значение и ковариацию RetExact с входами (ExpReturn и ExpCovariance), вы заметите, что они почти идентичны.
На данной точке RetExact и RetExpected оба являются массивами 504 на 5 на 2. Теперь примите одинаково взвешенный портфель, сформированный из пяти активов, и создайте массивы портфельных возвратов, в которых каждый столбец представляет собой доходность портфеля соответствующего выборочного пути моделируемых возвратов из пяти активов. Массивы портфолио PortRetExact и PortRetExpected представляют собой 504 на 2 матрицы.
Weights = ones(NumAssets, 1)/NumAssets; PortRetExact = zeros(NumObs, NumSim); PortRetExpected = zeros(NumObs, NumSim); for i = 1:NumSim PortRetExact(:,i) = RetExact(:,:,i) * Weights; PortRetExpected(:,i) = RetExpected(:,:,i) * Weights; end
Наконец, преобразуйте моделируемые возвраты портфеля в цены и постройте график данных. В частности, обратите внимание, что с Exact метод соответствует ожидаемому возврату и ковариации, цены на портфель терминалов практически идентичны для каждого пути расчета. Это не соответствует действительности для Expected метод симуляции. Хотя в этом примере рассматриваются портфели, те же методы применяются и к отдельным активам. Таким образом, Exact симуляция наиболее целесообразно, когда для достижения тех же цен на терминалы требуются уникальные пути.
PortExact = ret2tick(PortRetExact, ... repmat(StartPrice,1,NumSim)); PortExpected = ret2tick(PortRetExpected, ... repmat(StartPrice,1,NumSim)); subplot(2,1,1), plot(PortExact, '-r') ylabel('Portfolio Prices') title('Exact Method') subplot(2,1,2), plot(PortExpected, '-b') ylabel('Portfolio Prices') title('Expected Method')
ExpReturn, ExpCovariance, и RetIntervalsЭтот пример показывает взаимодействие между ExpReturn, ExpCovariance, и RetIntervals. Напомним, что portsim моделирует коррелированные возвраты активов на интервале dt длины, заданные уравнением
где S - цена актива, μ - ожидаемая норма возврата, σ - волатильность цены актива, и ε представляет собой случайный результат стандартного нормального распределения.
Шаг dt времени определяется необязательным входом RetIntervals, либо как явный входной параметр, либо как единичный шаг по умолчанию. Независимо от периодичности ExpReturn, ExpCovariance, и RetIntervals должна быть последовательной. Для примера, если ExpReturn и ExpCovariance в годовом исчислении, затем RetIntervals должно быть через годы. Эта точка часто неправильно понимается.
Чтобы проиллюстрировать взаимодействие между ExpReturn, ExpCovariance, и RetIntervals, рассмотрите портфель из пяти активов со следующей ожидаемыми возвратами, стандартными отклонениями и корреляционной матрицей на основе ежедневных возвратов активов.
ExpReturn = [0.0246 0.0189 0.0273 0.0141 0.0311]/100;
Sigmas = [0.9509 1.4259 1.5227 1.1062 1.0877]/100;
Correlations = [1.0000 0.4403 0.4735 0.4334 0.6855
0.4403 1.0000 0.7597 0.7809 0.4343
0.4735 0.7597 1.0000 0.6978 0.4926
0.4334 0.7809 0.6978 1.0000 0.4289
0.6855 0.4343 0.4926 0.4289 1.0000];
Преобразуйте корреляции и стандартные отклонения в ковариацию матрицу ежедневных возвратов.
ExpCovariance = corr2cov(Sigmas, Correlations);
Предположим, что 252 торговых дня за календарный год и моделируйте одну выборку пути ежедневной доходности в течение четырехлетнего периода. Начиная с ExpReturn и ExpCovariance входы выражаются ежедневно, задаются RetIntervals = 1.
StartPrice = 100; NumObs = 1008; % four calendar years of daily returns RetIntervals = 1; % one trading day NumAssets = length(ExpReturn); randn('state',0); RetSeries1 = portsim(ExpReturn, ExpCovariance, NumObs, ... RetIntervals, 1, 'Expected');
Теперь аннуализируйте ежедневные данные, изменяя тем самым периодичность данных, путем умножения ExpReturn и ExpCovariance на 252 и разделение RetIntervals 252 (RetIntervals = 1/252 года). Сбросив генератор случайных чисел в его начальное состояние, можно воспроизвести результаты.
rng('default'); RetSeries2 = portsim(ExpReturn*252, ExpCovariance*252, ... NumObs, RetIntervals/252, 1, 'Expected');
Предположим, что одинаково взвешенные портфолио и вычислительные доходы портфеля сопоставлены с каждой моделируемой последовательностью возвратов.
Weights = ones(NumAssets, 1)/NumAssets; PortRet1 = RetSeries2 * Weights; PortRet2 = RetSeries2 * Weights;
Сравнение данных показывает, что PortRet1 и PortRet2 идентичны.
В этом примере показано, как симулировать одномерный геометрический процесс броуновского движения. Он основан на примере, найденном в Hull, опции, Futures, and Other Derivatives, 5th Edition (см. пример 12.2 на странице 236). В дополнение к проверке примера Халла, он также графически иллюстрирует lognormal свойство цен на акции терминала довольно большой симуляцией Монте-Карло.
Предположим, что вы владеете акцией с начальной ценой $20, годовой ожидаемым возвратом 20% и волатильностью 40%. Моделируйте дневной ценовой процесс для этого запаса в течение одного полного календарного года (252 торговых дня).
StartPrice = 20; ExpReturn = 0.2; ExpCovariance = 0.4^2; NumObs = 252; NumSim = 10000; RetIntervals = 1/252;
RetIntervals выражается в годах, согласующихся с тем, что ExpReturn и ExpCovariance в годовом исчислении. Кроме того, ExpCovariance вводится как отклонение, а не как более привычное стандартное отклонение (волатильность).
Установите состояние генератора случайных чисел и моделируйте 10 000 испытаний (реализаций) возвратов акций в течение полного календарного года в 252 торговых дня.
rng('default'); RetSeries = squeeze(portsim(ExpReturn, ExpCovariance, NumObs, ... RetIntervals, NumSim, 'Expected'));
The squeeze функция переформатирует выходной массив моделируемых возвратов из 252-by- 1-by- 10000 массив к более удобным 252-by- 10000 массив. (Напомним, что portsim является принципиально многомерным механизмом симуляции).
В соответствии с уравнениями Халла 12.4 и 12.5 на стр. 236
преобразуйте моделируемый ряд возвратов в ценовой ряд и вычислите среднее значение выборки и отклонение цен на конечные акции.
StockPrices = ret2tick(RetSeries, repmat(StartPrice, 1, NumSim)); SampMean = mean(StockPrices(end,:)) SampVar = var(StockPrices(end,:))
SampMean = 24.4489 SampVar = 101.4243
Сравните эти значения со значениями, которые вы получаете при помощи уравнений Халла.
ExpValue = StartPrice*exp(ExpReturn) ExpVar = ... StartPrice*StartPrice*exp(2*ExpReturn)*(exp((ExpCovariance)) - 1)
ExpValue = 24.4281 ExpVar = 103.5391
Эти результаты очень близки к результатам, показанным в примере 12.2 Халла.
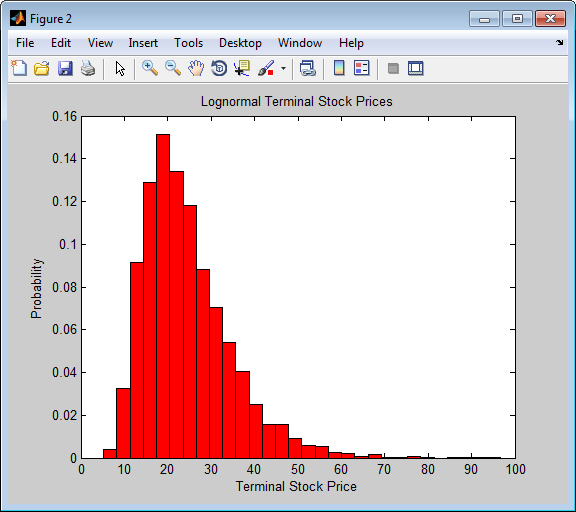
Отображение функции плотности выборки для конечной цены запаса по истечении одного календарного года. Из функции плотности выборки очевидно логнормальное распределение конечных цен акций.
[count, BinCenter] = hist(StockPrices(end,:), 30); figure bar(BinCenter, count/sum(count), 1, 'r') xlabel('Terminal Stock Price') ylabel('Probability') title('Lognormal Terminal Stock Prices')
[1] Hull, J. C. Опции, фьючерсы и другие производные. Prentice Hall, 2003.