Для любого значения во вселенной дискурса традиционная функция принадлежности 1 типа имеет одно значение принадлежности. Поэтому, хотя функция принадлежности 1 типа моделирует степень принадлежности к данному языковому набору, она не моделирует неопределенность в степени принадлежности. Чтобы смоделировать такую неопределенность, можно использовать функции принадлежности типа 2 интервала. В таких функциях членства 2 типа степень членства может иметь область значений значений.
Для примеров, которые используют системы нечеткого вывода типа 2, смотрите Нечеткое управление ПИД с Type-2 FIS и Предсказать хаотические временные ряды с использованием Type-2 FIS.
Функция принадлежности типа 2 интервала определяется функцией верхней и нижней принадлежности. Функция верхнего уровня (UMF) эквивалентна функции традиционного типа 1. Нижняя функция принадлежности (LMF) меньше чем или равна верхней функции принадлежности для всех возможных входных значений. Область между UMF и LMF является footprint of uncertainty (FOU). Следующая схема показывает UMF (красный), LMF (синий) и FOU (затененный) для треугольной функции принадлежности типа 2.
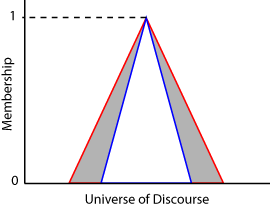
Для каждого входного значения во вселенной дискурса, степень принадлежности является областью значений значений между значениями LMF и UMF.
Используя программное обеспечение Fuzzy Logic Toolbox™, можно создать как системы нечеткого вывода Mamdani 2 типа, так и Sugeno.
В системах Мамдани типа 2 функции входа и выхода являются нечеткими наборами типа 2.
В системах Sugeno типа 2 только входы функции принадлежности являются нечеткими наборами типа 2. Выходы принадлежности те же, что и для системы Sugeno типа 1 - константа или линейная функция от входных значений.
Чтобы создать системы Mamdani и Sugeno 2 типа, используйте mamfistype2 и sugfistype2 объекты, соответственно. Эти объекты имеют те же параметры, что и тип-1 mamfis и sugfis объекты вместе с дополнительным TypeReductionMethod параметр.
Можно также создать систему нечеткого вывода типа 2 путем преобразования существующей системы типа 1, например, созданной с помощью genfis функция. Для этого используйте convertToType2 функция.
После создания системы нечеткого вывода типа 2 можно:
Оцените нечеткую систему, используя evalfis функции
Симулируйте нечеткую систему с помощью блока Fuzzy Logic Controller
Настройте параметры нечеткой системы, используя tunefis функция
Развертывание нечеткой системы как описано в Развертывание систем нечеткого вывода
Для систем нечеткого вывода типа 2 входные значения нечетки путем нахождения соответствующей степени принадлежности как в UMF, так и в LMF из предшествующего правила. Это генерирует два нечетких значения для каждой функции принадлежности 2 типа. Для примера нечеткость на следующем рисунке показывает значение принадлежности в верхней функции принадлежности (fU) и нижней функции принадлежности (fL).
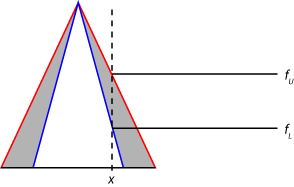
Далее, область значений сильных сторон запуска правила находят путем применения нечеткого оператора к нечетким значениям функций принадлежности типа 2, как показано на следующем рисунке. Максимальное значение этой области значений (wU) является результатом применения нечеткого оператора к нечетким значениям из UMFs. Минимальное значение (wL) является результатом применения нечеткого оператора к нечетким значениям из LMF
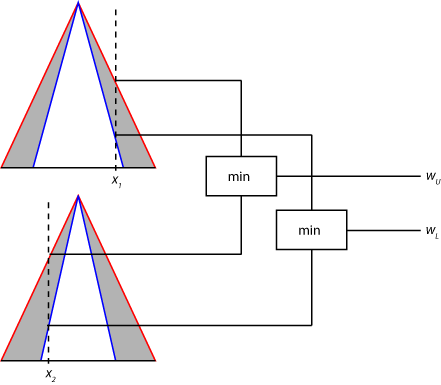
Обработка Antecedent одинаковая для систем Mamdani и Sugeno.
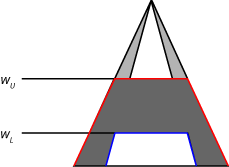
Для системы Мамдани клипы метода подразумевения (min implication) или шкалы (prod подразумевается) UMF и LMF выходной функции членства типа 2 с использованием пределов области значений запуска правила. Этот процесс создает выход нечеткое множество для каждого правила. Следующий рисунок показывает выходной нечеткий набор (темно-серая область), полученный при применении min последствия для UMF (красный) и LMF (синий).
Для системы Sugeno типа 2 выходной уровень, zi для i-го правила, вычисляется так же, как для системы Sugeno типа 1.
Здесь j является входным индексом, xj является значением j-й входной переменной, и c условия являются параметрами верхней функции принадлежности
В отличие от системы Sugeno типа 1, сильные стороны срабатывания правил не используются для обработки последствий каждого правила. Вместо этого в процессе агрегации используются уровни выхода и сильные стороны запуска правил.
Цель стадии агрегации состоит в том, чтобы вывести один нечеткий набор типа 2 из выходных нечетких наборов правил.
Для системы Mamdani типа 2 программное обеспечение находит совокупный нечеткий набор типа 2, применяя метод агрегации к UMF и LMF выходных нечетких наборов всех правил. Следующий рисунок показывает агрегирование двух нечетких наборов типа 2 (выходные выходы для системы с двумя правилами) с помощью max агрегирование.
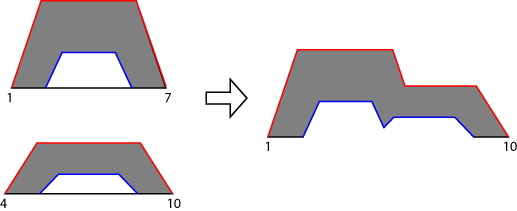
Для системы Sugeno типа 2 совокупный нечеткий набор получают с помощью следующих шагов:
Отсортируйте выходные уровни правил (zi) из всех правил в порядок возрастания. Эти значения выходного уровня определяют вселенную дискурса для совокупного нечеткого набора типа 2.
Для каждого выходного уровня задайте значение UMF, используя значение максимальной области значений включения из соответствующего правила.
Для каждого выходного уровня задайте значение LMF с помощью значения минимальной области значений включения из соответствующего правила.
Например, предположим, что у вас есть система Sugeno 2 типа с семью правилами. Кроме того, предположим, что эти правила имеют следующие выходы уровни и пределы области значений стрельбы.
| Правило | Выходной уровень (z) | Минимальное значение срабатывания | Максимальное значение включения |
|---|---|---|---|
| 1 | 6.3 | 0.1 | 0.5 |
| 2 | 4.9 | 0.4 | 0.5 |
| 3 | 1.6 | 0.3 | 0.5 |
| 4 | 5.8 | 0.5 | 0.7 |
| 5 | 5.4 | 0.2 | 0.6 |
| 6 | 0.7 | 0.5 | 0.8 |
| 7 | 3.2 | 0.2 | 0.7 |
Следующий рисунок показывает агрегированный нечеткий набор типа 2 для этой системы Sugeno с связанными с ней UMF (красный) и LMF (синий).
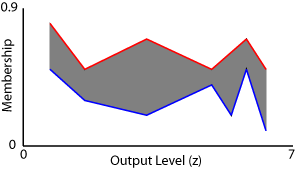
Чтобы найти окончательное четкое выходное значение для процесса вывода, совокупный нечеткий набор типа 2 сначала сводится к интервальному нечеткому набору типа 1, который является областью значений с нижними предельными cL и верхними предельными cR. Этот интервал типа 1 нечеткого набора обычно упоминается как центроид нечеткого набора типа 2. В теории этот центроид является средним значением центроидов всех нечетких множеств типа 1, встроенных в нечеткое множество типа 2. На практике невозможно вычислить точные значения cL и cR. Вместо этого для оценки этих значений используются итерационные методы сокращения типа.
Для заданного совокупного нечеткого множества типа 2 приблизительные значения cL и cR являются центроидами следующих нечетких множеств типа 1 (зеленого).
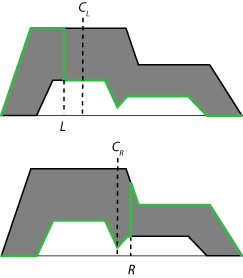
Математически эти центроиды найдены с помощью следующих уравнений. [1]
Здесь:
N - количество выборок, взятых в выходной области значений переменных, заданное с помощью evalfisOptions.
xi - i-я выходом значения.
μumf является верхней функцией членства.
μlmf является функцией более низкого уровня.
L и R являются switch points, которые оцениваются различными методами сокращения типа. Список поддерживаемых методов см. в разделе Методы сокращения типа.
Для обеих систем Мамдани и Сугено окончательное дефузифицированное выходное значение (y) является средним значением двух значений центроида из процесса сокращения типа.
Программное обеспечение Fuzzy Logic Toolbox поддерживает четыре встроенных метода сокращения типа. Эти алгоритмы различаются своими методами инициализации, допущениями, вычислительной эффективностью и условиями.
Чтобы задать метод сокращения типа для нечеткой системы типа 2, установите TypeReduction свойство mamfistype2 или sugfistype2 объект.
| Метод | TypeReduction Значение свойства | Описание |
|---|---|---|
| Карник-Мендель (КМ) [2] | "karnikmendel" | Разработан первый метод сокращения типа |
| Расширенный Карник-Мендель (EKM) [3] | "ekm" | Модификация алгоритма Карника-Менделя с улучшенной инициализацией, измененным условием завершения и улучшенной вычислительной эффективностью |
| Итерационный алгоритм с условием остановки (IASC) [4] | "iasc" | Итерационное усовершенствование методов грубой силы |
| Расширенный итерационный алгоритм с условием остановки (EIASC) [5] | "eiasc" | Улучшенная версия алгоритма IASC |
В целом вычислительная эффективность этих методов улучшается, когда вы перемещаетесь вниз по таблице.
Можно также использовать свой собственный пользовательский метод сокращения типа. Для получения дополнительной информации см. «Создание нечетких систем с использованием пользовательских функций».
[1] Мендель, Джерри М., Хани Хаграс, Воэй-Ван Tan, Уильям В. Мелек и Хао Ин. Введение в Type-2 нечеткого логического управления: теория и приложения. Хобокен, Нью-Джерси: IEEE Press, John Wiley & Sons, 2014.
[2] Карник, Нилеш Н. и Джерри М. Мендель. «Centroid of a Type-2 Fuzzy Set». Информационные науки 132, № 1-4 (февраль 2001): 195-220. https://doi.org/10.1016/S0020-0255 (01) 00069-X.
[3] Wu, D. and J.M. Mendel, «Enhanced Karnik-Mendel algorithms», IEEE Transactions on Fuzzy Systems, vol. 17, pp. 923-934. (2009)
[4] Duran, K., H. Bernal, and M. Melgarejo, «Улучшенный итерационный алгоритм вычисления обобщенного центроида интервального нечеткого набора типа 2», Annual Meeting of the North American Fuzzy Information Processing social, pp. 190-194. (2008)
[5] Wu, D. and M. Nie, «Сравнение и практические реализации алгоритмов сокращения типов для нечетких наборов и систем типа 2», Труды FUZZ-IEEE, стр. 2131-2138 (2011)