Оцените и проверьте нелинейные модели из данных single-input/single-output (SISO), чтобы найти ту, которая лучше всего представляет динамику вашей системы.
После завершения этого руководства вы сможете выполнить следующие задачи с помощью приложения System Identification:
Импорт объектов данных из MATLAB® рабочая область в приложение.
Оцените и проверьте нелинейные модели из данных.
Постройте и проанализируйте поведение нелинейностей.
В этом руководстве используется файл данных twotankdata.mat, который содержит данные временной области SISO для системы с двумя резервуарами, показанной на следующем рисунке.
Система с двумя резервуарами
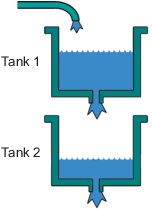
В системе с двумя резервуарами вода течет через трубопровод в бак 1, сливается в бак 2 и выходит из системы через небольшое отверстие в нижней части бака 2. Измеренный вход u (t) к системе является напряжением, приложенным к насосу, который подает воду в бак 1 (в вольтах). Измеренный выход y (t) - высота воды в нижнем баке (в метрах).
Основываясь на законе Бернулли, который утверждает, что вода, протекающая через небольшое отверстие на дне бака, зависит нелинейно от уровня воды в баке, вы ожидаете, что отношение между входными и выходными данными будет нелинейным.
twotankdata.mat включает 3000 выборки со шаг расчета 0,2 с.
Можно оценить нелинейные модели черного ящика в дискретном времени для данных как с одним выходом, так и с несколькими выходами во временной области. Можно выбрать из двух типов нелинейных структур модели черного ящика:
Нелинейные модели ARX
Модели Гаммерштейна-Винера
Примечание
Вы можете оценить модели черного ящика Гаммерштейна-Винера только из входных/выходных данных. Эти модели не поддерживают данные timeseries, где нет входов.
Для получения дополнительной информации об оценке нелинейных моделей черного ящика, см. «Нелинейная идентификация модели».
Нелинейная модель ARX состоит из регрессоров модели и выходной функции. Выходная функция включает линейные и нелинейные функции, которые действуют на регрессоры модели, чтобы дать выход модели и фиксированное смещение для этого выхода. Этот блок представляет структуру нелинейной модели ARX в сценарии симуляции.
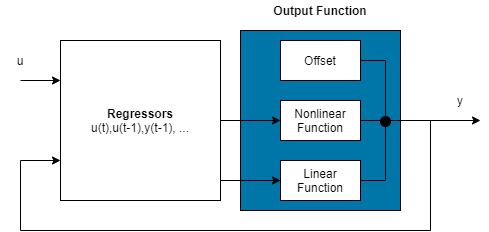
Программа вычисляет выходные y нелинейной модели ARX в два этапа:
Он вычисляет значения регрессора из текущих и прошлых входных значений и прошлых выходных данных.
В самом простом случае регрессоры являются задержанными входами и выходами, такими как u (t -1) и y (t -3). Такие регрессоры называются linear regressors. Линейные регрессоры задаются с помощью linearRegressor объект. Можно также задать линейные регрессоры при помощи линейных порядков моделей ARX в качестве входного параметра. Для получения дополнительной информации см. «Нелинейные порядки модели ARX» и «Задержка». Однако этот второй подход ограничивает набор регрессоров линейными регрессорами с последовательными задержками. Чтобы создать polynomial regressors, используйте polynomialRegressor объект. Можно также задать custom regressors, которые являются нелинейными функциями задержанных входов и выходов. Например, u (t -1) y (t -3) является пользовательским регрессором, который умножает образцы входа и выхода вместе. Задайте пользовательские регрессоры, используя customRegressor объект.
Можно назначить любой из регрессоров в качестве входов линейному функциональному блоку выходной функции, нелинейному функциональному блоку или обоим.
Он преобразует регрессоры в выходные данные модели с помощью блока выходной функции. Блок выходной функции может включать линейные и нелинейные блоки параллельно. Для примера рассмотрим следующее уравнение:
Здесь x является вектором регрессоров, а r - средним значением x. - выход блока линейной функции. представляет выход нелинейного функционального блока. Q является проекционной матрицей, которая делает вычисления хорошо обусловленными. d является скалярным смещением, которое добавляется к комбинированным выходам линейного и нелинейного блоков. Точная форма F (x) зависит от вашего выбора выходной функции. Можно выбрать из доступных объектов отображения, таких как сети древовидного раздела, вейвлет и многослойные нейронные сети. Можно также исключить из выходной функции линейный или нелинейный функциональный блок.
При оценке нелинейной модели ARX программное обеспечение вычисляет значения параметров модели, такие как L, r, d, Q и другие параметры, задающие g.
Получившиеся нелинейные модели ARX idnlarx объекты, которые хранят все данные модели, включая регрессоры модели и параметры выходной функции. Для получения дополнительной информации об этих объектах см. Раздел «Нелинейные структуры модели».
Этот блок представляет структуру модели Гаммерштейна-Винера:

Где,
f - нелинейная функция, которая преобразовывает входные данные u (<reservedrangesplaceholder5>) как w (<reservedrangesplaceholder3>) = f (u (<reservedrangesplaceholder0>)).
w (t), внутренняя переменная, является выходом блока Input Nonlinearity и имеет ту же размерность, что и u (t).
B/F является линейной передаточной функцией, которая преобразует w (t) как x (t) = (B/F) w (t).
x (t), внутренняя переменная, является выходом Линейного блока и имеет ту же размерность, что и y (t).
B и F подобны полиномам в линейной модели Output-Error. Для получения дополнительной информации о моделях вывода-ошибки смотрите Что такое полиномиальные модели?.
Для ny выходов и nu входов линейный блок является матрицей передаточной функции, содержащей записи:
где j = 1,2,...,ny и i = 1,2,...,nu.
h является нелинейной функцией, которая преобразует выход линейного блочного x (t) в выходной y системы (t) как y (t) = h (x (t)).
Поскольку f действует на входе порт линейного блока, эта функция называется входом нелинейностью. Точно так же, поскольку h действует на выходе порт линейного блока, эта функция называется выходом нелинейностью. Если ваша система содержит несколько входов и выходов, необходимо задать функции f и h для каждого входного и выходного сигнала. Вы не должны включать как вход, так и выход нелинейность в структуру модели. Когда модель содержит только входные f нелинейности, она называется Hammerstein моделью. Точно так же, когда модель содержит только выходные h нелинейности, она называется моделью Винера.
Программное обеспечение вычисляет выходные y модели Гаммерштейна-Винера в три этапа:
Вычислите w (t) = f (u (t)) от входных данных.
w (t) является входом в линейную передаточную функцию B/F.
Входная нелинейность является статической (безпамятной) функцией, где значение выхода в заданный временной t зависит только от входного значения в t времени.
Можно сконфигурировать нелинейность входа как сигмоидную сеть, вейвлет сеть, насыщение, мертвую зону, кусочно-линейную функцию, одномерный полином или пользовательскую сеть. Можно также удалить вход нелинейность.
Вычислите выход линейного блока с помощью w (t) и начальных условий: x (t) = (B/F) w (t).
Можно сконфигурировать линейный блок, задав порядки B числителя и F знаменателя.
Вычислите модель, произведенную, преобразовав выход линейного блока x (<reservedrangesplaceholder6>) использование нелинейной функции h как y (<reservedrangesplaceholder3>) = h (x (<reservedrangesplaceholder0>)).
Подобен вход нелинейности, выход нелинейность является статической функцией. Можно сконфигурировать нелинейность выхода так же, как и нелинейность входа. Можно также удалить выход нелинейность, так что y (t) = x (t).
Получившиеся модели idnlhw объекты, которые хранят все данные модели, включая параметры модели и оценки нелинейности. Для получения дополнительной информации об этих объектах см. Раздел «Нелинейные структуры модели».
Загрузите выборочные данные в twotankdata.mat путем ввода следующей команды в Командном Окне MATLAB:
load twotankdata
Эта команда загружает следующие две переменные в браузер Рабочее Пространство MATLAB:
u - входные данные, которое является напряжением, приложенным к насосу, который подает воду в бак 1 (в вольтах).
y - выходные данные, представляющие собой уровень воды в баке 2 (в метрах).
System Identification Toolbox™ объекты данных инкапсулируют как значения данных, так и свойства данных в одну сущность. Можно использовать команды System Identification Toolbox, чтобы удобно манипулировать этими объектами данных как отдельными сущностями.
Вы, должно быть, уже загрузили выборочные данные в Рабочее пространство MATLAB, как описано в Загрузке данных в Рабочее пространство MATLAB.
Используйте следующие команды, чтобы создать две iddata объекты данных, ze и zv, где ze содержит данные для оценки модели и zv содержит данные для валидации модели. Ts - шаг расчета.
Ts = 0.2; % Sample time is 0.2 sec z = iddata(y,u,Ts); % First 1000 samples used for estimation ze = z(1:1000); % Remaining samples used for validation zv = z(1001:3000);
Чтобы просмотреть свойства iddata объект, использовать get команда. Для примера:
get(ze)
MATLAB возвращает следующие свойства и значения данных:
Domain: 'Time'
Name: ''
OutputData: [1000x1 double]
y: 'Same as OutputData'
OutputName: {'y1'}
OutputUnit: {''}
InputData: [1000x1 double]
u: 'Same as InputData'
InputName: {'u1'}
InputUnit: {''}
Period: Inf
InterSample: 'zoh'
Ts: 0.2000
Tstart: 0.2000
SamplingInstants: [1000x0 double]
TimeUnit: 'seconds'
ExperimentName: 'Exp1'
Notes: {}
UserData: []Для изменения свойств данных используйте запись через точку. Для примера, чтобы назначить имена каналов и модулей, которые маркируют оси графика, введите следующий синтаксис в Командном окне MATLAB:
% Set time units to minutes ze.TimeUnit = 'sec'; % Set names of input channels ze.InputName = 'Voltage'; % Set units for input variables ze.InputUnit = 'V'; % Set name of output channel ze.OutputName = 'Height'; % Set unit of output channel ze.OutputUnit = 'm'; % Set validation data properties zv.TimeUnit = 'sec'; zv.InputName = 'Voltage'; zv.InputUnit = 'V'; zv.OutputName = 'Height'; zv.OutputUnit = 'm';
Чтобы проверить, что InputName свойство ze изменен, введите следующую команду:
ze.inputname
Совет
Имена свойства, такие как InputName, не чувствительны к регистру. Можно также сокращать имена свойства, начинающиеся с Input или Output путем подстановки u для Input и y для Output в имени свойства. Для примера, OutputUnit эквивалентно yunit.
Чтобы открыть приложение System Identification, введите следующую команду в Командном окне MATLAB:
systemIdentification
Имя сеанса по умолчанию, Untitled, появляется в строке заголовка.
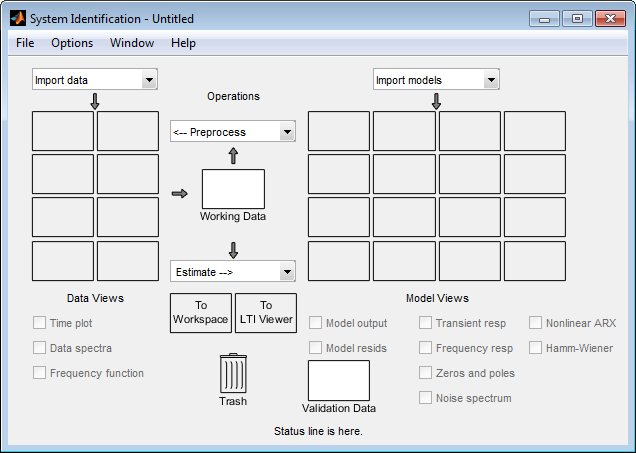
Можно импортировать объекты данных в приложение из рабочего пространства MATLAB.
Вы должны были уже создать объекты данных, как описано в Создании объектов iddata, и открыть приложение, как описано в Start the Система Идентификации App.
Для импорта объектов данных:
В приложении System Identification выберите Import data > Data object.
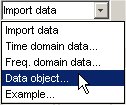
Это действие открывает диалоговое окно Импорт данных.
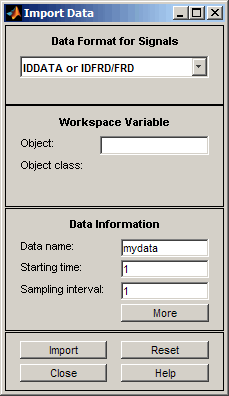
Введите ze в поле Object для импорта данных оценки. Нажмите Enter.
Это действие вводит информацию об объекте в поля Import Data.
Щелкните More, чтобы просмотреть дополнительную информацию об этих данных, включая имена каналов и модулей.
Щелкните Import, чтобы добавить значок с именем ze в приложение System Identification.
В диалоговом окне «Импорт данных» введите zv в поле Object для импорта данных валидации. Нажмите Enter.
Щелкните Import, чтобы добавить значок с именем zv в приложение System Identification.
В диалоговом окне «Импорт данных» нажмите кнопку Close.
В приложении System Identification перетащите значок zv данных валидации в Validation Data прямоугольник. Значок ze данных оценки уже обозначен в Working Data прямоугольнике.
Также щелкните правой кнопкой мыши по zv значок для открытия диалогового окна Данные/Информация о модели (Data/model Info). Установите флажок Use as Validation Data. Нажмите Apply, а затем Close, чтобы добавить zv к Validation Data прямоугольнику.
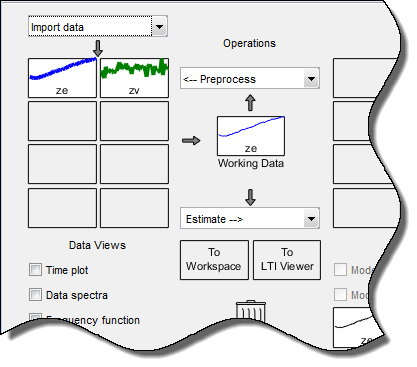
Теперь System Identification приложение напоминает следующий рисунок.
В этом фрагменте руководства вы оцениваете нелинейную модель ARX с помощью структуры модели по умолчанию и опций оценки.
Необходимо, чтобы данные уже были подготовлены, как описано в разделе «Подготовка данных». Для получения дополнительной информации о нелинейных моделях ARX, см. «Что такое нелинейная модель ARX?».
Примечание
Рисунки в этом руководстве представляют типичное System Identification приложение сеанса. Ваши результаты могут точно не совпадать с результатами на изображениях.
В приложении System Identification выберите Estimate > Nonlinear models.
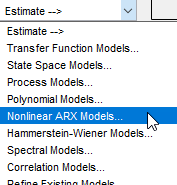
Это действие открывает диалоговое окно Estimate Nonlinear ARX Models.
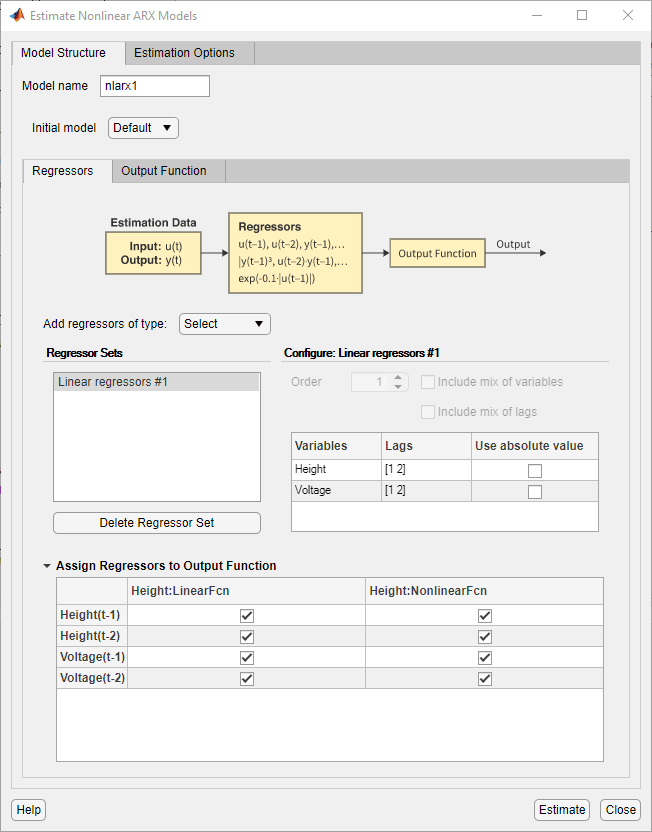
Диалоговое окно содержит две вкладки - Model Structure и Estimation Options.
Вкладка Model Structure содержит параметры, которые конфигурируют структуру модели, такие как выбор регрессоров и тип выходной функции. Укажите имя модели, которая будет оценена в Model name. Имя модели по умолчанию nlarx1.
Используйте вкладку Regressors, чтобы создать наборы регрессоров для использования. По умолчанию приложение создает линейный регрессор с лагами [1 2] в каждой переменной и сохраняет регрессор как Linear regressors #1 в области Regressor Sets. Эта панель содержит таблицу, которая позволяет изменять лаги, используемые для каждой переменной.
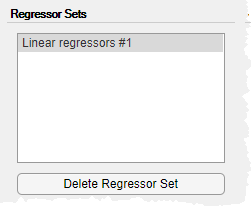
Панель строения Configure: Linear regressors #1 содержит таблицу, в которой показаны значения задержки, используемые в наборе регрессоров. Можно изменить эти лаги.
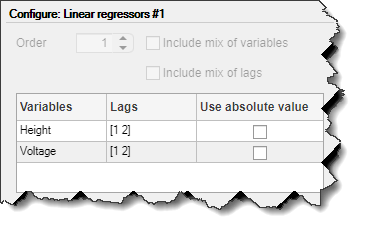
В таблице Assign Regressors to Output Function назначений регрессора перечислены имена регрессора и назначения регрессора компонентам выходной функции.
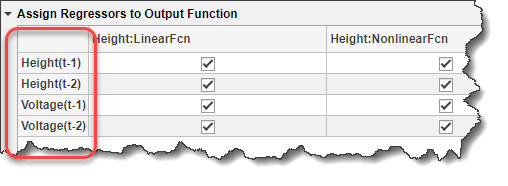
Назначения регрессора в таблице создают модель для выхода Height из:
Height (<reservedrangesplaceholder9>) = f (Height (t-1), Height (t-2) , Voltage (t-1), Voltage (t-2))
Здесь f (.) является статической нелинейной функцией, которая преобразует регрессоры в выходные. Чтобы выбрать f (.) и связанные с ним параметры, используйте вкладку Output Function.
Можно добавить больше наборов регрессоров, таких как полиномы и пользовательские формулы, выбрав тип регрессора в Add regressors of type.
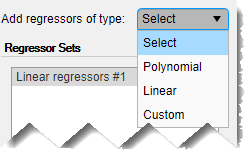
Этот пример использует только Linear regressors #1.
Выберите вкладку Output Function.
Вкладка показывает, что приложение выбирает Wavelet Network как тип по умолчанию выходной функции f (.). Эта функция использует сумму линейной функции, нелинейную функцию (которая является суммой масштабированных вейвлеты) и член смещения, чтобы вычислить выход. На вкладке также показан набор параметров конфигурации. Количество вейвлетов, используемых функцией, конфигурируется таким образом, чтобы оно выбиралось автоматически во время оценки. Этот выбор можно изменить. Можно также изменить начальные значения линейных коэффициентов и смещения. Для первой оценки сохраните варианты по умолчанию.
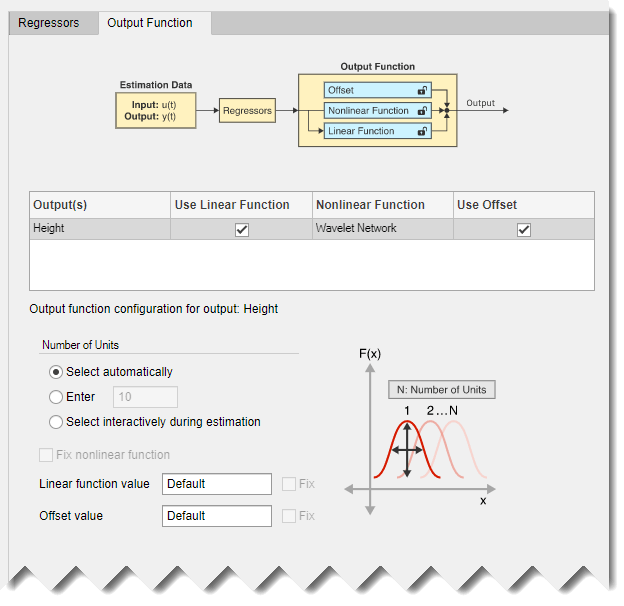
Нажмите Estimate.
Это действие добавляет модель nlarx1 на модельную плату System Identification приложения, как показано на следующем рисунке.
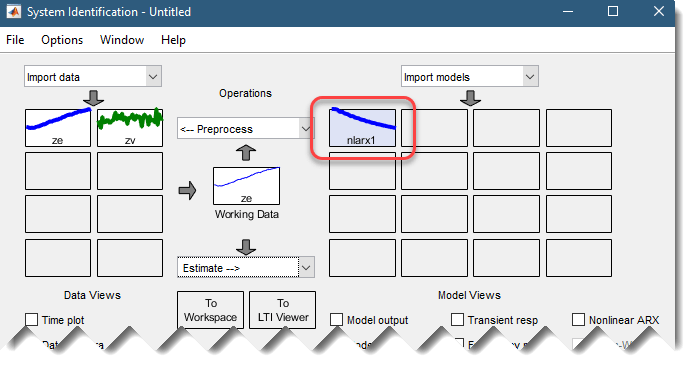
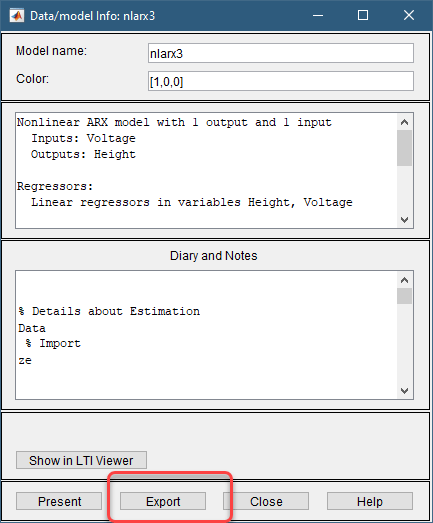
Дважды нажатие кнопки или щелкните правой кнопкой мыши значок модели nlarx1 Плата модели показывает информацию о предполагаемой модели. Верхняя область описывает структуру модели и результаты оценки (используемые данные, процент подгонки и другие метрики качества). В нижней области (Diary and Notes) показан скрипт MATLAB, который можно использовать, чтобы воспроизвести результаты оценки в командной строке.
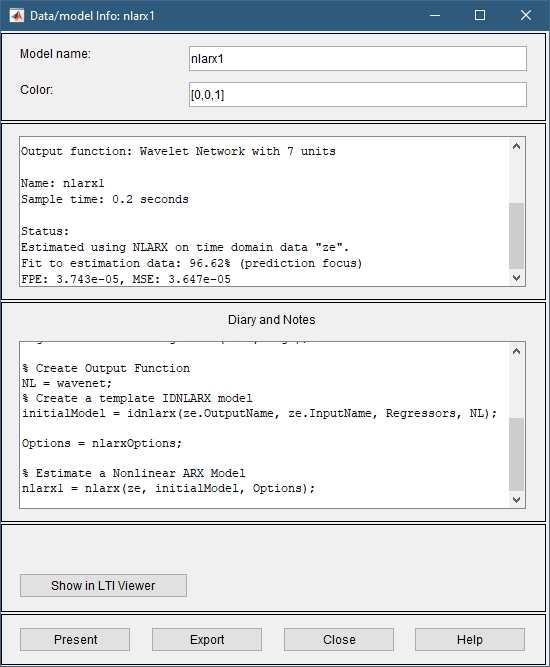
Примечание
Fit (%) вычисляется с использованием набора данных оценки с предсказанием особого внимания. а не набор данных валидации. Однако выходной график модели на следующем шаге сравнивает подгонку с набором данных валидации. Чтобы увидеть, насколько хорошо модель может симулировать ответ независимого набора данных валидации, используйте Model Output график, как обсуждается на следующем шаге.
В области Model Views приложения System Identification выберите Model output. Это действие симулирует модель, используя входные данные валидации в качестве входных данных для модели и строит графики моделируемого выхода поверх выходных данных валидации.
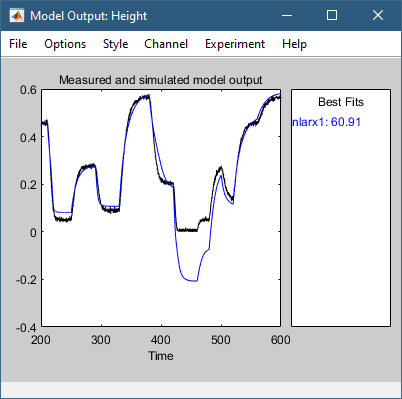
Область Best Fits выходного графика модели показывает согласие между выходом модели и выходными данными валидации с помощью нормализованной среднеквадратичной (NRMSE) метрики качества подгонки. Соглашение является плохим в 400-500 промежутке времени.
Выполните следующую процедуру, чтобы просмотреть форму нелинейности как функцию регрессоров на графике нелинейной модели ARX.
В приложении System Identification установите флажок Nonlinear ARX , чтобы просмотреть сечения нелинейности.
По умолчанию на графике показана связь между выходными регрессорами Height(t-1) и Height(t-2). Этот график показывает регулярную плоскость на следующем рисунке. Таким образом, отношение между регрессорами и выходом является приблизительно линейной плоскостью.
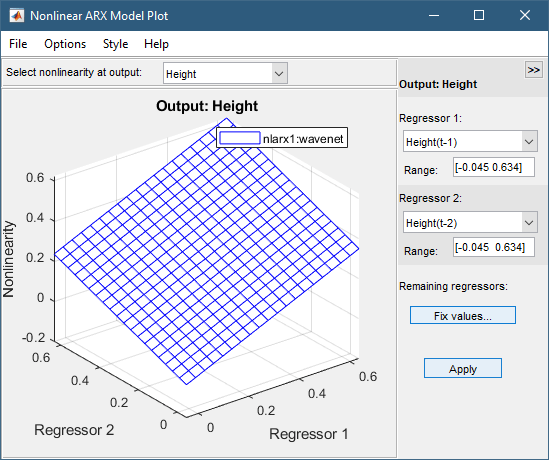
В окне Нелинейная модель ARX Plot задайте Regressor 1 Voltage(t-1). Установите Regressor 2 значение Voltage(t-2). Нажмите Apply.
Отношение между этими регрессорами и выходом нелинейно, как показано на следующем графике.
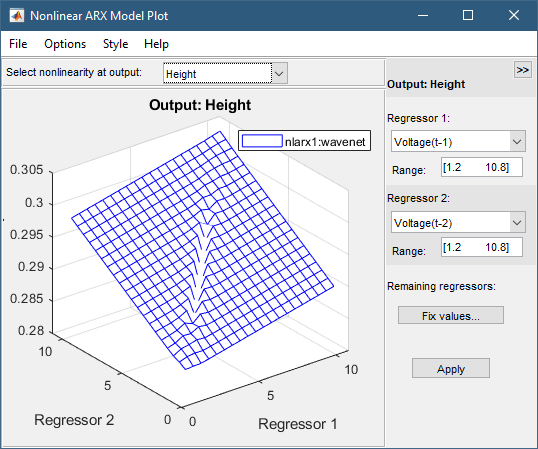
Чтобы повернуть поверхность нелинейности, выберите Style > Rotate 3D и перетащите график в новую ориентацию.
Чтобы отобразить 1-D сечение для регрессора 1, установите для регрессора 2 значение none, и нажмите Apply. Следующий рисунок показывает полученную величину нелинейности для Регрессора 1, которая представляет сдвинутый во времени сигнал напряжения Voltage(t-1).
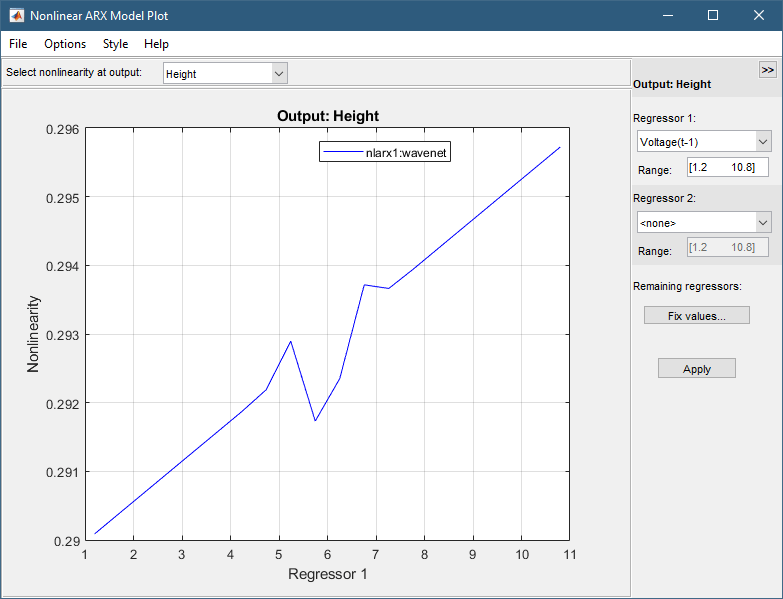
В этом фрагменте руководства вы оцениваете нелинейную модель ARX с определенными настройками входной задержки и нелинейности. Обычно вы выбираете порядки модели методом проб и ошибок, пока не получите модель, которая производит точную подгонку к данным.
Вы должны были уже оценить нелинейную модель ARX с настройками по умолчанию, как описано в Оценке нелинейной модели ARX с Настройками по умолчанию.
В диалоговом окне Estimate Nonlinear ARX Models выберите вкладку Model Structure, а затем - вкладку Regressors.
На панели Configure: Linear regressors #1 измените Voltage переменная lags to [3 4]. Это связано с тем, что данные предполагают, что между входом и выходом есть минимум 3 отставания выборки.
Это действие обновляет список регрессоров, чтобы показать Voltage(t-3) и Voltage(t-4)- сроки с минимальной задержкой в три выборки.
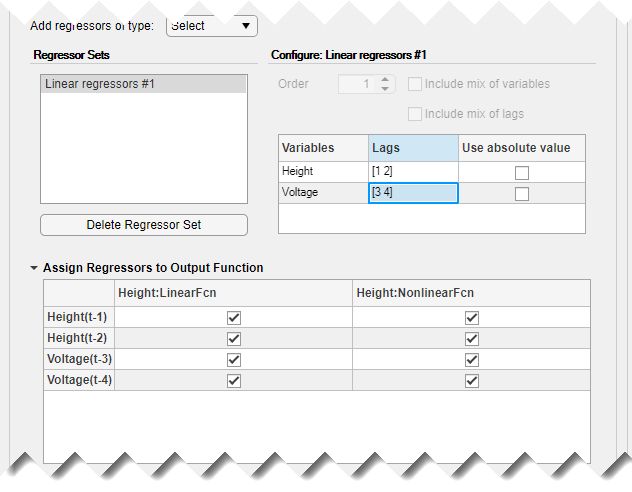
Нажмите Estimate.
Это действие добавляет модель nlarx2 в приложение System Identification и обновляет окно Model Output, чтобы включить эту модель. Двойной клик по nlarx2 значок на панели моделей главного окна приложения показывает результаты оценки.
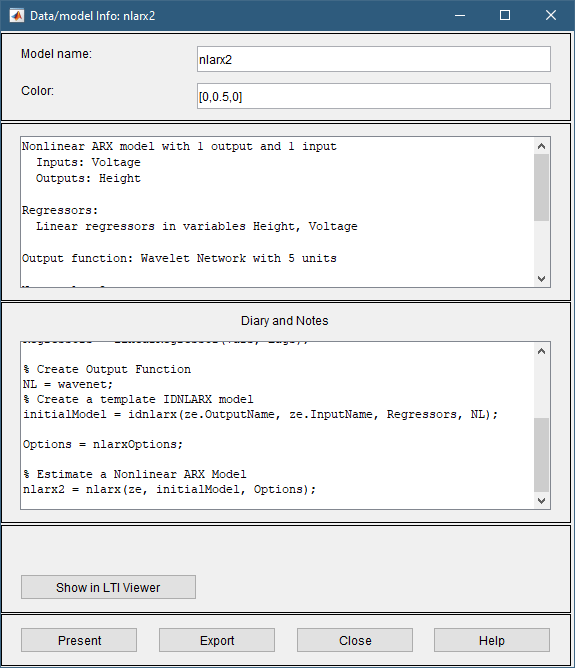
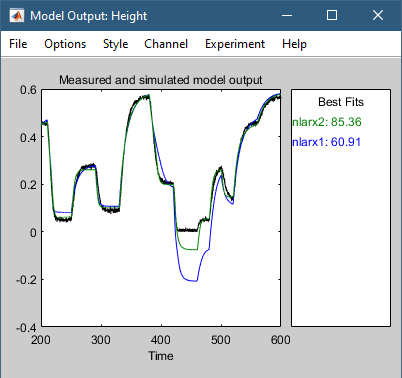
Приложение также обновляет выходной график модели, чтобы отобразить подгонку модели nlarx2 в набор данных валидации zv. График показывает, что выбор правильной входной переменной лагов улучшает подгонку.
В диалоговом окне Estimate Nonlinear ARX Models выберите вкладку Model Structure, а затем - вкладку Regressors.
Выберите вкладку Output Function.
Для Number of Units выберите Enter и введите 6. Установка определенного числа управляет гибкостью нелинейной функции, непосредственно задавая количество вейвлеты, которые Wavelet Network использует.
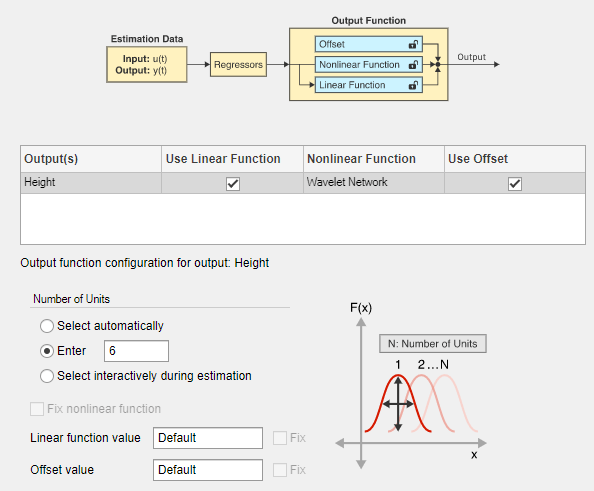
Нажмите Estimate.
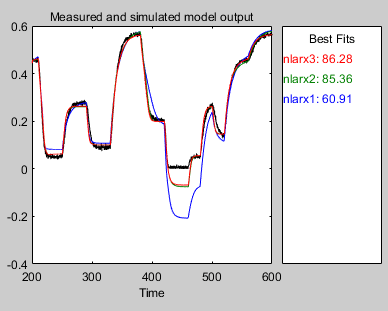
Это действие добавляет модель nlarx3 на System Identification приложения. Также обновляется окно Model Output, как показано на следующем рисунке.
Можно оценить нелинейную модель ARX, которая использует более высокие степени отстающих переменных в качестве регрессоров. В этом примере вы добавите полиномы второго порядка переменных с отставанием, включая перекрестные условия.
В диалоговом окне Estimate Nonlinear ARX Models выберите вкладку Model Structure и затем выберите вкладку Regressors.
Разверните Add regressors of type и выберите Polynomial.
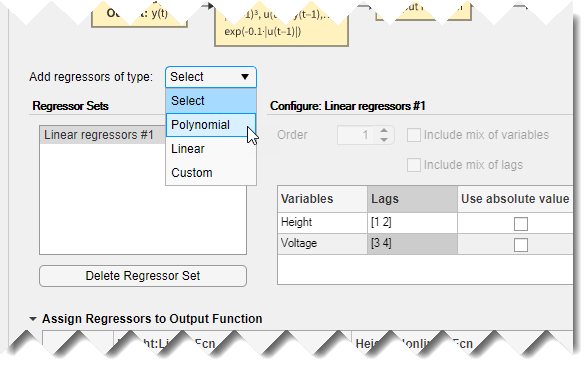
Это действие добавляет набор полиномиальных регрессоров, называемый Polynomial regressors #1 в список наборов регрессоров. По умолчанию этот набор сконфигурирован для генерации регрессоров порядка 2, как показано на панели строения.
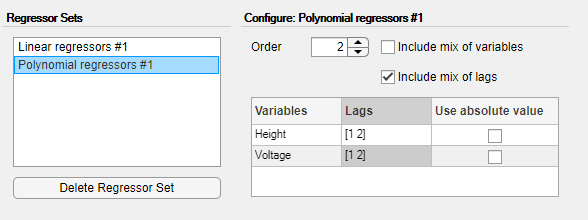
Измените Voltage задержки в [3 4].
Выберите Include mix of variables, чтобы включить все перекрестные условия. Это действие добавляет к модели десять регрессоров второго порядка, в дополнение к четырем, представленным Linear regressor #1.
Нажмите Estimate. Это действие добавляет модель nlarx4 к приложению Приложение обновляет график Model Output, как показано на следующем рисунке.
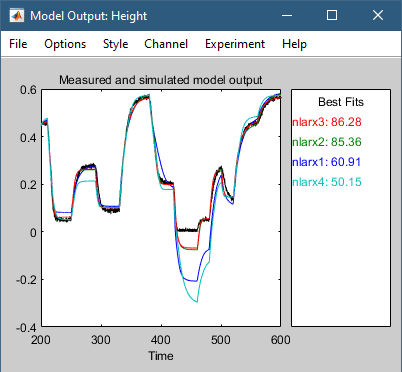
График показывает, что сложение полиномиальных регрессоров не улучшило обобщающую способность модели. То есть модель не обеспечивает лучшую подгонку между выходом модели и измеренным выходом для независимых данных валидации. Этот результат обычно является сценарием с избыточными стандартами, то есть, когда модель содержит больше регрессоров, чем абсолютно необходимо.
Можно оценить нелинейную модель ARX, которая включает только подмножество регрессоров, которые входят как входы в нелинейный блок. По умолчанию все регрессоры используются в нелинейном блоке. В этом фрагменте руководства вы присваиваете только подмножество регрессоров нелинейному блоку.
Вы должны были уже задать структуру модели, как описано в Change Nonlinear ARX Model Structure.
В диалоговом окне Estimate Nonlinear ARX Models выберите вкладку Model Structure, а затем - вкладку Regressors.
Если свернуть, разверните панель Assign Regressors to Output Function.
Снимите флажки для всех регрессоров второго порядка из Height:NonlinearFcn столбца таблицы. Кроме того, очистите выбор для всех регрессоров с перекрестными терминами (то есть регрессоры, состоящие из продуктов 2 членов) из Height:LinearFcn
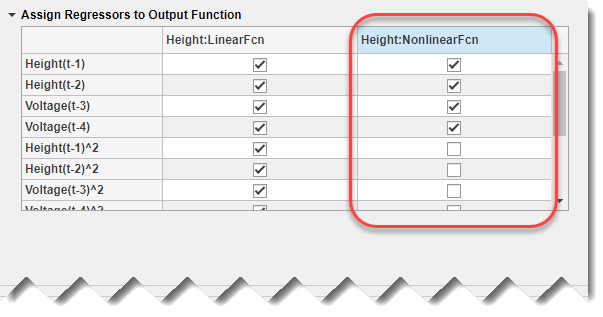
Нажмите Estimate.
Это действие добавляет модель nlarx5 к System Identification приложению. это также обновляет окно Model Output.
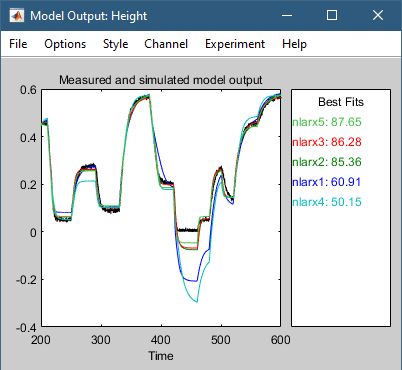
Эта модель показывает улучшенную обобщающую способность.
Можно оценить серию нелинейных моделей ARX, сделав систематические изменения структуры модели и основав каждую новую модель на строении ранее оцененной модели. В этом фрагменте руководства вы оцениваете нелинейную модель ARX, которая похожа на существующую модель (nlarx3), но который имеет другую нелинейность в выходной функции.
В диалоговом окне Estimate Nonlinear ARX Models выберите вкладку Model Structure.
Выберите nlarx3 от Initial Model. Это устанавливает свойства, которые отображаются на вкладках Regressors и Output Function, на значения, соответствующие nlarx3.
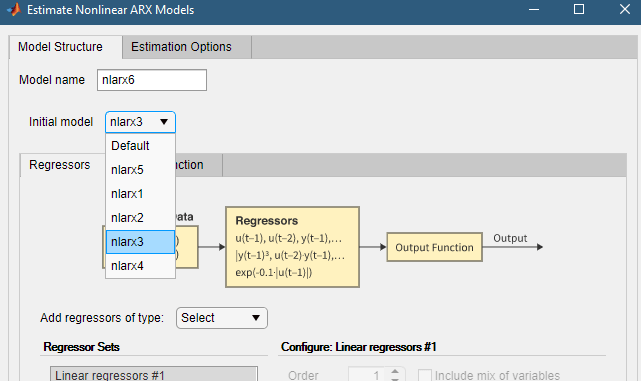
Выберите вкладку Output Function.
В таблице измените выбор Nonlinear Function на Sigmoid Network. Это устанавливает выходную функцию в сигмоидную сеть.
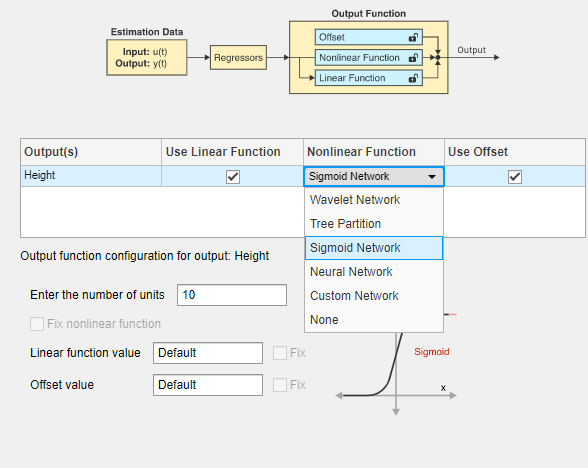
В Enter the number of units введите 6.
Нажмите Estimate.
Это действие добавляет модель nlarx6 к System Identification приложения. Он также обновляет график Model Output, как показано на следующем рисунке.
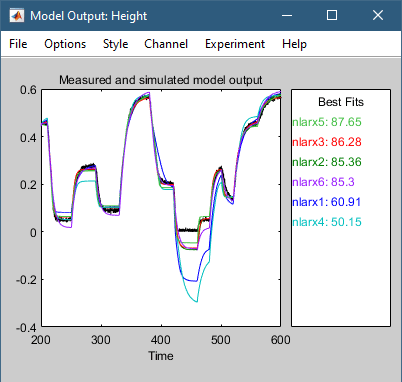
Лучшая модель является самой простой моделью, которая точно описывает динамику. Результаты указывают на то, что модель nlarx3 является кандидатом на то, чтобы быть лучшей моделью idnlarx для этих данных, основанной на различных вариантах структуры модели, которые исследовал этот пример.
Перетащите nlarx3 значок в поле To Workspace в главном окне приложения System Identification. Также дважды нажатие кнопки nlarx3 значок для открытия информационной доски. Оттуда щелкните Export, чтобы экспортировать модель в базовое рабочее пространство.
В этом фрагменте руководства вы оцениваете нелинейные модели Гаммерштейна-Винера с помощью структуры модели по умолчанию и опций оценки.
Необходимо, чтобы данные уже были подготовлены, как описано в разделе «Подготовка данных». Для получения дополнительной информации о нелинейных моделях ARX, смотрите Что такое модель Гаммерштейна-Винера?
Примечание
Рисунки в этом руководстве представляют типичное System Identification приложение сеанса. Ваши результаты могут точно не совпадать с результатами на изображениях.
В приложении System Identification выберите Estimate > Hammerstein-Wiener Models, чтобы открыть диалоговое окно Estimate Hammerstein-Wiener Models. Диалоговое окно содержит две вкладки - Model Structure и Estimation Options.
Смотрите структуру модели по умолчанию. Вкладка Model Structure содержит три вкладки, по одной вкладке для каждого компонента модели. Эти компоненты являются входом нелинейностью, линейным динамическим блоком и выходом нелинейностью.
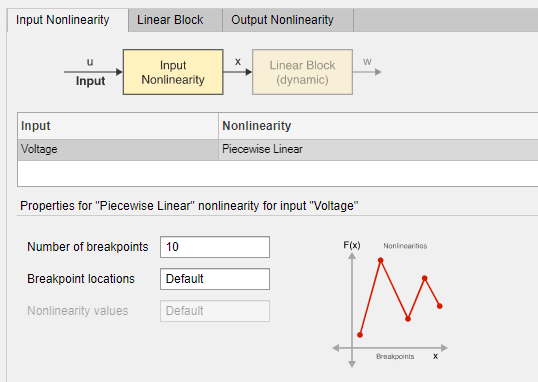
Выберите вкладку Input Nonlinearity. Нелинейностью по умолчанию является функция Piecewise Linear с 10 точками прерывания.
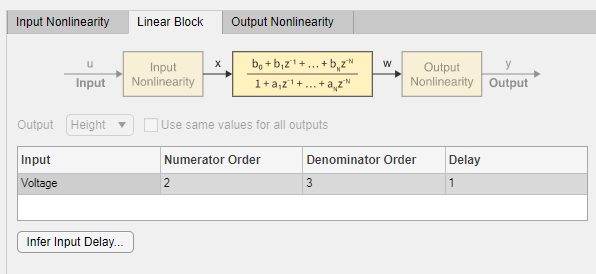
Выберите вкладку Linear Block. Линейная передаточная функция имеет порядок числителя 2, что подразумевает полином второго порядка в z-1, порядок знаменателя 3 и задержка на входе 1 выборка.
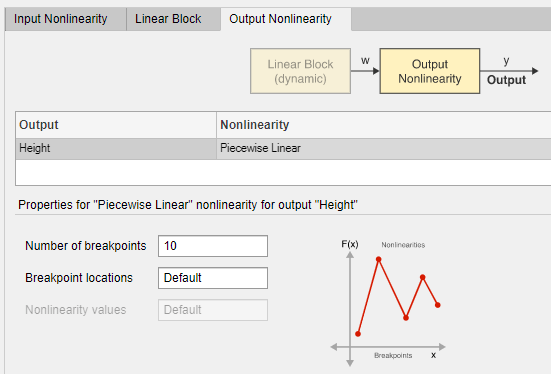
Выберите вкладку Output Nonlinearity. Как и на вкладке Input Nonlinearity, нелинейность по умолчанию является функцией Piecewise Linear с 10 точками прерывания.
Нажмите Estimate.
Это действие оценивает параметры модели Гаммерштейна-Винера, чтобы минимизировать различие между выходом модели и измеренным выходом (ze.OutputData). Предполагаемые параметры:
Местоположения точек останова (координаты x и y) входных и выходных кусочно-линейных функций.
Числитель и знаменатель полинома коэффициенты, которые составляют линейный блок передаточную функцию.
Программное обеспечение добавляет предполагаемую модель nlhw1 к модельной доске приложения System Identification.
В приложении System Identification установите флажок Model output.
Это действие симулирует модель, используя входные данные валидации в качестве входных данных для модели и строит графики моделируемого выхода поверх выходных данных валидации. Обратите внимание, что для данных валидации задано значение zv.
Область Best Fits окна Model Output показывает согласие между выходом модели и выходными данными валидации.
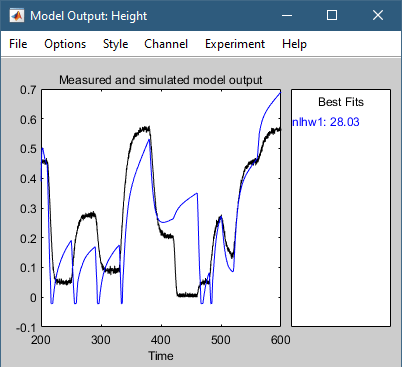
Модель nlhw1 не проверяет хорошо. Подгонка к zv.OutputData беден.
Можно построить график нелинейности ввода/вывода и линейной передаточной функции модели на графике Гаммерштейна-Винера.
В приложении System Identification выберите Hamm-Wiener, чтобы просмотреть график модели Гаммерштейна-Винера.
График отображает вход нелинейность, как показано на следующем рисунке.
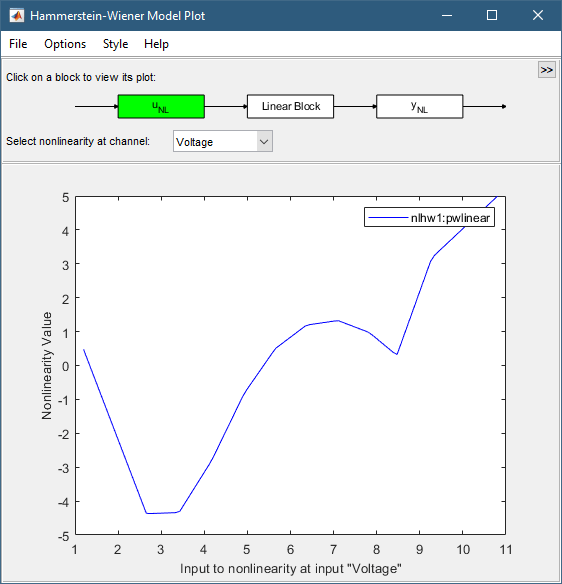
Щелкните на yNL прямоугольнике в верхнем фрагменте окна Hammerstein-Wiener Model Plot.
График обновляется, чтобы отобразить выход нелинейность.
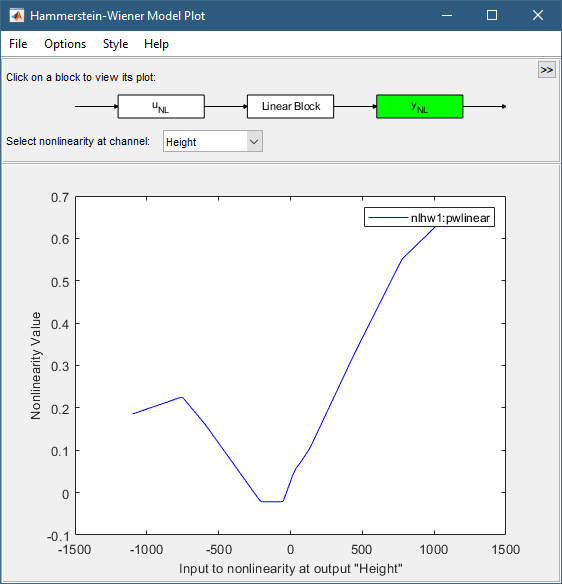
Щелкните на Linear Block прямоугольнике в верхнем фрагменте окна Hammerstein-Wiener Model Plot.
График обновляется, чтобы отобразить переходную характеристику линейной передаточной функции.
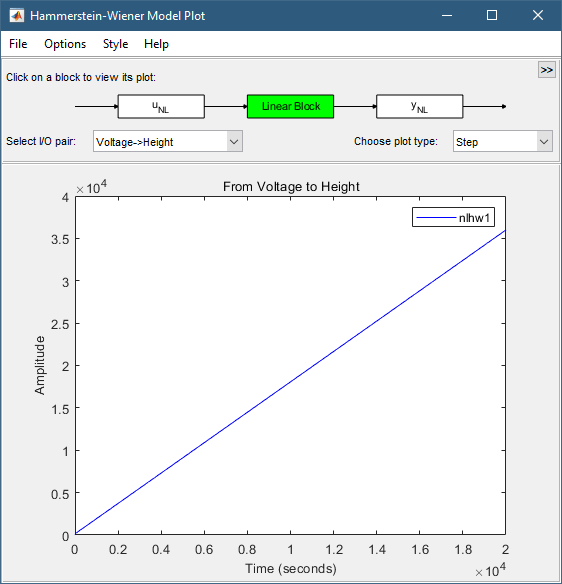
В списке Choose plot type выберите Bode. Это действие отображает диаграмму Боде линейной передаточной функции.
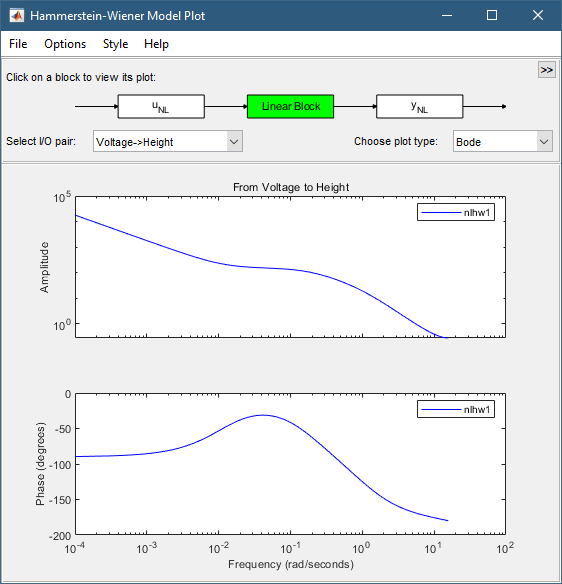
В этом фрагменте руководства вы оцениваете модель Гаммерштейна-Винера с определенным порядком модели и настройками нелинейности. Обычно вы выбираете порядки моделей и задержки путем проб и ошибок, пока не получите модель, которая производит удовлетворительную подгонку к данным.
Вы должны были уже оценить модель Гаммерштейна-Винера с настройками по умолчанию, как описано в Оценке моделей Гаммерштейна-Винера с настройками по умолчанию.
В диалоговом окне Estimate Hammerstein-Wiener выберите вкладку Model Structure, а затем вкладку Linear Block.
Для Voltage Входом канале дважды кликните соответствующую < reservedrangesplaceholder1 > камеру и введите значение 3.
Нажмите Estimate.
Это действие добавляет модель nlhw2 в приложение System Identification и обновляет график Model Output, как показано на следующем рисунке.
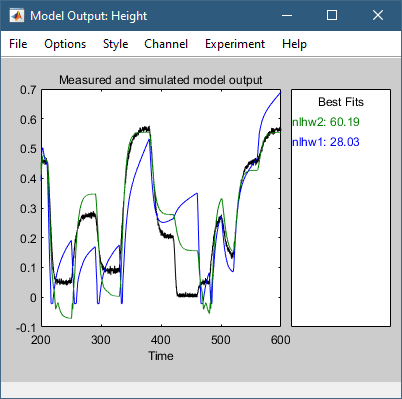
Панель Best Fits окна Model Output показывает качество nlhw2 подгонка, что является улучшением по сравнению с моделью nlhw1.
В этом фрагменте примера вы изменяете структуру модели Гаммерштейна-Винера по умолчанию, меняя ее оценку нелинейности.
Совет
Если вы знаете, что ваша система включает в себя насыщение или нелинейность мертвой зоны, можно задать эти специализированные оценки нелинейности в вашей модели. Piecewise Linear, Wavelet Network, и Sigmoid Network являются оценщиками нелинейности для общего нелинейного приближения.
В диалоговом окне Estimate Hammerstein-Wiener Models выберите вкладку Model Structure, а затем вкладку Input Nonlinearity.
Щелкните Nonlinearity камеры для Voltage переменная и выберите Sigmoid Network из списка.
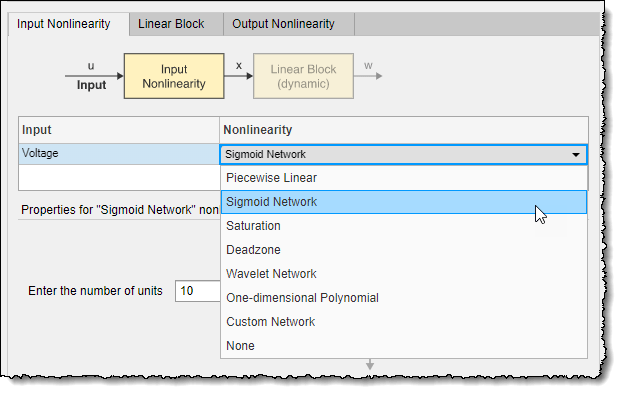
В Enter the number of units установите значение 20.
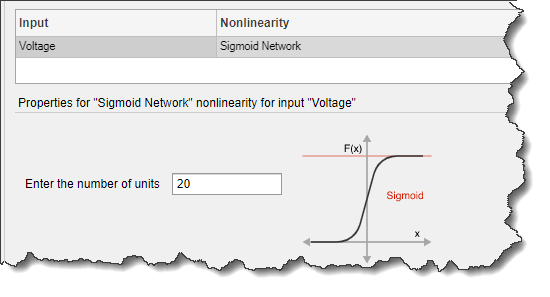
Нажмите Estimate.
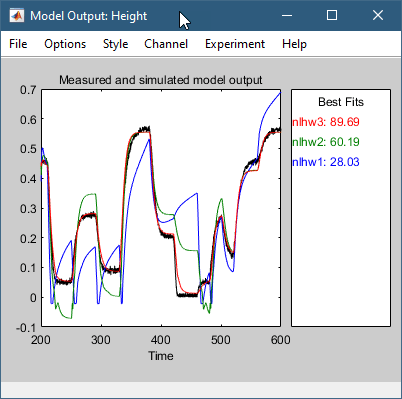
Это действие добавляет модель nlhw3 на System Identification приложения. Также обновляется окно Model Output, как показано на следующем рисунке.
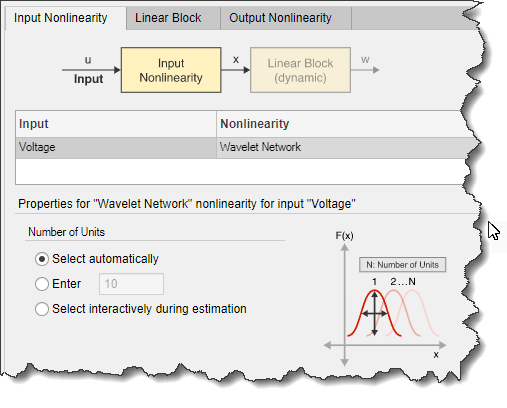
В диалоговом окне Estimate Hammerstein-Wiener Models выберите вкладку Input Nonlinearity.
Для Voltage введите, установите Nonlinearity равным Wavelet Network. Значение по умолчанию для Number of Units является Select Automatically.
Выберите вкладку Output Nonlinearity.
Установите Height выход Nonlinearity в One-dimensional Polynomial. Установите Degree of polynomial значение 2.
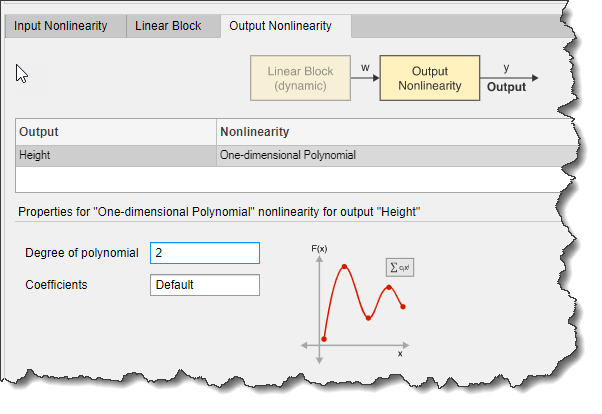
Нажмите Estimate.
Это действие добавляет модель nlhw4 на System Identification приложения. Также обновляется окно Model Output, как показано на следующем рисунке.
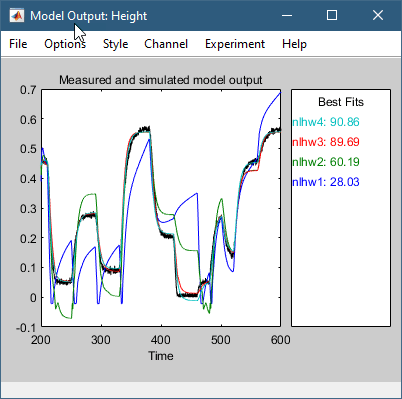
Лучшая модель является самой простой моделью, которая точно описывает динамику.
В этом примере модели nlhw3 и nlhw4 хорошие кандидаты.