Exponenta Banner

idnlarx

Нелинейная модель ARX

развернуть все на странице

Описание

Система координат idnlarx модель представляет нелинейную модель ARX, которая является расширением линейной структуры ARX и содержит линейные и нелинейные функции.

Нелинейная модель ARX состоит из регрессоров модели и выходной функции. Выходная функция включает линейные и нелинейные функции, которые действуют на регрессоры модели, чтобы дать выход модели и фиксированное смещение для этого выхода. Этот блок представляет структуру нелинейной модели ARX в сценарии симуляции.

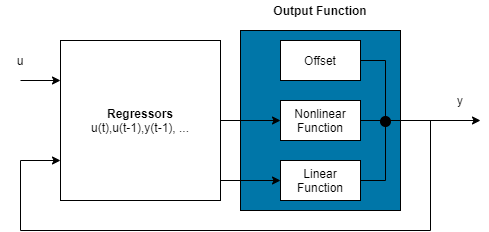
Regressor block is on the left. Output function is on the right. Output function block contains, from top to bottom, Offset, Nonlinear Function, and Linear Function. The inputs to the Regressor block are system input u and the output of the output function y.

Программа вычисляет выходные y нелинейной модели ARX в два этапа:

  1. Он вычисляет значения регрессора из текущих и прошлых входных значений и прошлых выходных данных.

    В самом простом случае регрессоры являются задержанными входами и выходами, такими как u (t -1) и y (t -3). Такие регрессоры называются linear regressors. Линейные регрессоры задаются с помощью linearRegressor объект. Можно также задать линейные регрессоры при помощи линейных порядков моделей ARX в качестве входного параметра. Для получения дополнительной информации см. «Нелинейные порядки модели ARX» и «Задержка». Однако этот второй подход ограничивает набор регрессоров линейными регрессорами с последовательными задержками. Чтобы создать polynomial regressors, используйте polynomialRegressor объект. Можно также задать custom regressors, которые являются нелинейными функциями задержанных входов и выходов. Например, u (t -1) y (t -3) является пользовательским регрессором, который умножает образцы входа и выхода вместе. Задайте пользовательские регрессоры, используя customRegressor объект.

    Можно назначить любой из регрессоров в качестве входов линейному функциональному блоку выходной функции, нелинейному функциональному блоку или обоим.

  2. Он преобразует регрессоры в выходные данные модели с помощью блока выходной функции. Блок выходной функции может включать линейные и нелинейные блоки параллельно. Для примера рассмотрим следующее уравнение:

    F(x)=LT(x−r)+g(Q(x−r))+d

    Здесь x является вектором регрессоров, а r - средним значением x. F(x)=LT(x−r)+y0 - выход блока линейной функции. g(Q(x−r))+y0 представляет выход нелинейного функционального блока. Q является проекционной матрицей, которая делает вычисления хорошо обусловленными. d является скалярным смещением, которое добавляется к комбинированным выходам линейного и нелинейного блоков. Точная форма F (x) зависит от вашего выбора выходной функции. Можно выбрать из доступных объектов отображения, таких как сети древовидного раздела, вейвлет и многослойные нейронные сети. Можно также исключить из выходной функции линейный или нелинейный функциональный блок.

    При оценке нелинейной модели ARX программное обеспечение вычисляет значения параметров модели, такие как L, r, d, Q и другие параметры, задающие g.

Получившиеся нелинейные модели ARX idnlarx объекты, которые хранят все данные модели, включая регрессоры модели и параметры выходной функции. Для получения дополнительной информации об этих объектах см. Раздел «Нелинейные структуры модели».

Для получения дополнительной информации о idnlarx структура модели, см. Что такое нелинейные модели ARX?

Для idnlarx свойства объекта, см. Свойства.

Создание

Можно получить idnlarx объект одним из двух способов.

  • Используйте nlarx команда для создания idnlarx объект и оценка параметров модели.

    sys = nlarx(data,reg)

  • Используйте idnlarx конструктор, чтобы создать нелинейную модель ARX и затем оценить параметры модели используя nlarx или pem.

    sys = idnlarx(output_name,input_name,reg)

Синтаксис

sys = idnlarx(output_name,input_name,orders)
sys = idnlarx(output_name,input_name,Regressors)
sys = idnlarx(___,OutputFcn)
sys = idnlarx(linmodel)
sys = idnlarx(linmodel,OutputFcn)
sys = idnlarx(___,Name,Value)

Описание

Задайте модель непосредственно

пример

sys = idnlarx(output_name,input_name,orders) задает набор линейных регрессоров, использующих порядки модели ARX. Используйте этот синтаксис, когда вы расширяете линейную модель ARX или когда вы планируете использовать только регрессоры, которые являются линейными с последовательными лагами.

пример

sys = idnlarx(output_name,input_name,Regressors) создает нелинейную модель ARX с выходными и входными именами output_name и input_name, соответственно, и набор регрессоров в регрессорах, который содержит любую комбинацию линейных, полиномиальных и пользовательских регрессоров. Программное обеспечение создает sys использование вейвлет по умолчанию ('wavenet') объект отображения для выходной функции.

пример

sys = idnlarx(___,OutputFcn) задает выходную функцию OutputFcn, которая преобразует регрессоры в выходы модели. Можно использовать этот синтаксис с любыми предыдущими комбинациями входных аргументов.

Инициализируйте значения модели с помощью линейной модели

пример

sys = idnlarx(linmodel) использует линейную модель linmodel извлечения некоторых свойств, таких как имена, модули и шаг расчета, и инициализации значений линейных коэффициентов модели. Используйте этот синтаксис, когда вы хотите создать нелинейную модель ARX как расширение или улучшение существующей линейной модели.

пример

sys = idnlarx(linmodel,OutputFcn) задает выходную функцию OutputFcn, которая преобразует регрессоры в выходы модели.

Задайте свойства модели

sys = idnlarx(___,Name,Value) задает дополнительные свойства idnlarx моделировать структуру с помощью одного или нескольких аргументов в виде имя-значение.

Входные параметры

расширить все

Порядки модели ARX, заданные как матрица [na nb nk]. na обозначает количество отложенных выходов, nb обозначает количество запаздывающих входов и nk обозначает минимальную входную задержку. Минимальная выходная задержка фиксирована на 1. Для получения дополнительной информации о том, как создать orders матрица, см. arx.

Когда вы задаете orders, программное обеспечение преобразует информацию о порядке в линейную форму регрессора в idnlarx Regressors свойство. Для получения примера смотрите Создание нелинейной модели ARX с использованием Порядков ARX Model.

Линейная модель, заданная в дискретном времени как любая линейная модель, созданная с помощью оценок, то есть idpoly объект, idss объект, idtf объект, или idproc объект с Ts > 0. Создайте эту модель с помощью функции конструктора для объекта или оцените модель с помощью связанной команды оценки. Для примера, чтобы создать модель ARX, используйте arx, и задайте результат idpoly объект как linmodel.

Свойства

расширить все

Спецификация регрессора, заданная как вектор-столбец, содержащая один или несколько объектов спецификации регрессора, которые являются linearRegressor объекты, polynomialRegressor объекты, и customRegressor customRegressor объекты. Каждый объект задает формулу для генерации регрессоров из отстающих переменных. Для примера:

  • L = linearRegressor({'y1','u1'},{1,[2 5]}) генерирует регрессоры y1 (t -1), u1 (t -2) и u2 (t -5).

  • P = polynomialRegressor('y2',4:7,2) генерирует регрессоры y2 (t -4)2, y2 (t –5)2, y2 (t –6)2, и y2 (t-7)2.

  • C = customRegressor({'y1','u1','u2'},{1 2 2},@(x,y,z)sin(x.*y+z)) генерирует один регрессор sin (y1 (t -1) u1 (t -2) + u2 (t -2)

    .

Пример, реализующий эти регрессоры, см. в разделе Создание и объединение типов регрессоров.

Чтобы добавить регрессоры к существующей модели, создайте вектор объектов спецификации и используйте запись через точку для того, чтобы задать Regressors к этому вектору. Для примера следующий код сначала создает idnlarx модели sys и затем добавляет объекты регрессора L, P, и C к регрессорам sys.

sys = idnlarx({'y1','y2'},{'u1','u2'});
R = [L;P;C];
sys.Regressors = R;

Пример создания и использования линейного набора регрессоров см. в разделе Создание нелинейной модели ARX с использованием линейных регрессоров.

Выходная функция, которая отображает регрессоры idnlarx модель в выходы модели, заданная как массив столбцов, содержащий нуль или более из следующих строк или объектов отображения:

'wavenet' или wavenet объектВейвлет
'linear' или '' или [] или linear объектЛинейная функция
'sigmoidnet' или sigmoidnet объектСигмоидная сеть
'treepartition' или treepartition объектБинарная модель регрессии древовидного разбиения
neuralnet объектНейронная сеть - Сеть прямого распространения Toolbox™ Глубокого Обучения.
customnet объектНастраиваемая сеть - аналогично sigmoidnet, но с определяемой пользователем заменой сигмоидной функции.

wavenet, sigmoidnet, treepartion, и customnet объекты содержат как линейные, так и нелинейные компоненты. Можно удалить (не использовать) линейные компоненты wavenet, sigmoidnet, и customnet путем установки LinearFcn.Use значение в false.

neuralnet функция имеет только нелинейный компонент, который network (Deep Learning Toolbox) объекта Deep Learning Toolbox. Линейная функция, как подразумевается в имени, имеет только линейный компонент.

Установка вектора символов, для примера 'sigmoidnet'создает объект отображения с настройками по умолчанию. Также можно задать отображение свойств объекта двумя другими способами:

  • Создайте объект отображения с помощью аргументов для изменения свойств по умолчанию.

    MO = sigmoidnet(15)

  • Сначала создайте объект отображения по умолчанию, а затем используйте запись через точку для изменения свойств.

    MO = sigmoidnet;
MO.NumberOfUnits = 15

Для ny выходных каналов можно задать объекты отображения индивидуально для каждого канала путем установки OutputFcn в массив ny отображения объектов. Для примера следующий код задает OutputFcn использование записи через точку для системы с двумя входными каналами и двумя выходными каналами. 

sys = idnlarx({'y1','y2'},{'u1','u2'});
sys.OutputFcn = [wavenet; sigmoidnet]
Чтобы задать одно и то же отображение для всех выходов, задайте OutputFcn как вектор символов или один объект отображения.

OutputFcn представляет статическую функцию отображения, которая преобразует регрессоры нелинейной модели ARX в выходы модели. OutputFcn является статическим, потому что это не зависит от времени. Для примера, если y(t)=y0+a1y(t−1)+a2y(t−2)+…+b1u(t−1)+b2u(t−2)+…, затем OutputFcn является линейной функцией, представленной linear объект.

Для примера определения выходной функции см. «Задание выходной функции для нелинейной модели ARX».

Назначения регрессора линейным и нелинейным компонентам нелинейной модели ARX, заданные как nr таблица -by nc с логическими записями, которые определяют, какие регрессоры использовать для какого компонента. Здесь nr количество регрессоров. nc - общее количество линейных и нелинейных компонентов в OutputFcn. Строки таблицы соответствуют отдельным регрессорам. Для имен строк заданы имена регрессора. Если значение таблицы для i строк и j индекса компонентов true, тогда i-й регрессор является входом в линейный или нелинейный j компонента .

Для мультивыходов, OutputFcn содержит по одному объекту отображения для каждого выхода. Каждый объект отображения может использовать как линейные, так и нелинейные компоненты или только один из двух компонентов.

Пример просмотра и изменения RegressorUsage свойство, см. «Изменение назначений регрессора в компонентах выходной функции».

Это свойство доступно только для чтения.

Сводный отчет, который содержит информацию об опциях оценки и результатах для нелинейной модели ARX, полученной с помощью nlarx команда. Использование Report для поиска оценочной информации для идентифицированной модели, включая:

  • Метод оценки

  • Опции оценки

  • Условия окончания поиска

  • Оценка данной подгонки

Содержимое Report нерелевантны, если модель была построена с использованием idnlarx.

sys = idnlarx('y1','u1',reg);
sys.Report.OptionsUsed
ans =

     []

Если вы используете nlarx для оценки модели, полей Report содержат информацию о данных оценки, опциях и результатах.

load iddata1;
sys = nlarx(z1,reg);
m.Report.OptionsUsed
Option set for the nlarx command:

  IterativeWavenet: 'auto'
             Focus: 'prediction'
           Display: 'off'
    Regularization: [1x1 struct]
      SearchMethod: 'auto'
     SearchOptions: [1x1 idoptions.search.identsolver]
      OutputWeight: 'noise'
          Advanced: [1x1 struct]

Для получения дополнительной информации об этом свойстве и о том, как его использовать, смотрите Выходные Аргументы в nlarx страница с описанием и отчет по оценке.

Независимая переменная для входов, выходов и - при наличии - внутренних состояний, заданная как вектор символов.

Noise отклонения (ковариация матрица) инноваций модели e. Алгоритм оценки обычно устанавливает это свойство. Однако можно также присвоить ковариационные значения путем определения ny-by- ny матрица.

Шаг расчета, заданная как положительная скалярная величина, представляющая период дискретизации. Это значение выражается в модуле, заданной как TimeUnit свойство модели.

Модули измерения для временной переменной, шага расчета Ts, и любые задержки в модели, заданные как одно из следующих значений:

  • 'nanoseconds'

  • 'microseconds'

  • 'milliseconds'

  • 'seconds'

  • 'minutes'

  • 'hours'

  • 'days'

  • 'weeks'

  • 'months'

  • 'years'

Изменение этого свойства не влияет на другие свойства и, следовательно, изменяет общее поведение системы. Использовать chgTimeUnit (Control System Toolbox) для преобразования между единицами времени без изменения поведения системы.

Входные имена каналов, заданные как одно из следующих:

  • Вектор символов - Для моделей с одним входом, например, 'controls'.

  • Массив ячеек из символьных векторов - Для мультивходов.

Входные имена в нелинейных моделях ARX должны быть действительными MATLAB® имена переменных после удаления любых пространств.

Кроме того, используйте автоматическое расширение вектора, чтобы назначить входные имена для мультивходов. Для примера, если sys является моделью с двумя входами, введите:

sys.InputName = 'controls';

Имена входа автоматически расширяются на {'controls(1)';'controls(2)'}.

Когда вы оцениваете модель, используя iddata объект, dataпрограммное обеспечение автоматически устанавливает InputName на data.InputName.

Можно использовать сокращённое обозначение u для ссылки на InputName свойство. Для примера, sys.u эквивалентно sys.InputName.

Входные имена каналов имеют несколько применений, включая:

  • Идентификация каналов на отображении модели и графиках

  • Извлечение подсистем систем MIMO

  • Определение точек соединения при соединении моделей

Входные модули канала, заданные как один из следующих:

  • Вектор символов - Для моделей с одним входом, например, 'seconds'.

  • Массив ячеек из символьных векторов - Для мультивходов.

Использование InputUnit отслеживать модули входных сигналов. InputUnit не влияет на поведение системы.

Входные группы каналов. The InputGroup свойство позволяет вам назначить входные каналы систем MIMO в группы и ссылаться на каждую группу по имени. Задайте входные группы как структуру. В этой структуре имена полей являются именами групп, а значения полей - входными каналами, принадлежащими каждой группе. Для примера:

sys.InputGroup.controls = [1 2];
sys.InputGroup.noise = [3 5];

создает входные группы с именем controls и noise которые включают входные каналы 1, 2 и 3, 5, соответственно. Затем можно извлечь подсистему из controls входы для всех выходов с помощью:

sys(:,'controls')

Выходы каналов, заданные как одно из следующих:

  • Вектор символов - Для моделей с одним выходом. Для примера, 'measurements'.

  • Массив ячеек из символьных векторов - Для мультивыход моделей.

Выходы имена в нелинейных моделях ARX должны быть допустимыми Переменным MATLAB имен после удаления любых пространств.

Кроме того, используйте автоматическое расширение вектора, чтобы назначить имена выходов для мультивыходов. Для примера, если sys является двухвыпускной моделью, введите:

sys.OutputName = 'measurements';

Выходы данных автоматически расширяются на {'measurements(1)';'measurements(2)'}.

Когда вы оцениваете модель, используя iddata объект, dataпрограммное обеспечение автоматически устанавливает OutputName на data.OutputName.

Можно использовать сокращённое обозначение y для ссылки на OutputName свойство. Для примера, sys.y эквивалентно sys.OutputName.

Имена выходных каналов имеют несколько применений, включая:

  • Идентификация каналов на отображении модели и графиках

  • Извлечение подсистем систем MIMO

  • Определение точек соединения при соединении моделей

Выход модулей канала, заданный как один из следующих:

  • Вектор символов - Для моделей с одним выходом. Для примера, 'seconds'.

  • Массив ячеек из символьных векторов - Для мультивыход моделей.

Использование OutputUnit отслеживать выход модулей сигнала. OutputUnit не влияет на поведение системы.

Выходы каналов. The OutputGroup свойство позволяет вам назначить выходные каналы систем MIMO в группы и ссылаться на каждую группу по имени. Задайте выходные группы как структуру. В этой структуре имена полей являются именами групп, а значения полей - выходными каналами, принадлежащими каждой группе. Для примера:

sys.OutputGroup.temperature = [1];
sys.InputGroup.measurement = [3 5];

создает выходные группы с именем temperature и measurement которые включают выходные каналы 1, и 3, 5, соответственно. Затем можно извлечь подсистему из всех входов в measurement выходы с использованием:

sys('measurement',:)

Имя системы, заданное как вектор символов. Для примера, 'system 1'.

Любой текст, который вы хотите связать с системой, заданный как строка или массив ячеек из векторов символов. Свойство сохраняет любой тип данных, которые вы предоставляете. Для образца, если sys1 и sys2 являются динамические системы моделями, можно задать их Notes свойства следующим образом.

sys1.Notes = "sys1 has a string.";
sys2.Notes = 'sys2 has a character vector.';
sys1.Notes
sys2.Notes
ans = 

    "sys1 has a string."


ans =

    'sys2 has a character vector.'

Любые данные, которые вы хотите связать с системой, заданные как любой тип данных MATLAB.

Функции объекта

Для получения информации о функциях объекта для idnlarx, см. Нелинейные модели ARX.

Примеры

свернуть все

Открыть Live Script

Создайте idnlarx модель путем определения вектора порядка модели ARX.

Создайте вектор порядка формы [na nb nk], где na и nb являются порядками полиномов модели A и B ARX и nk количество задержек ввода/вывода.

na = 2;
nb = 3;
nk = 5;
orders = [na nb nk];

Создайте нелинейную модель ARX sys.

output_name = 'y1';
input_name = 'u1';

sys = idnlarx(output_name,input_name,[2 3 5]);

Просмотрите выходную функцию.

disp(sys.OutputFcn)
Wavelet Network

 Nonlinear Function: Wavelet network with number of units chosen automatically.
 Linear Function: uninitialized
 Output Offset: uninitialized

           Input: [1×1 idpack.Channel]
          Output: [1×1 idpack.Channel]
       LinearFcn: [1×1 nlident.internal.UseProjectedLinearFcn]
    NonlinearFcn: [1×1 nlident.internal.WavenetFcn]
          Offset: [1×1 nlident.internal.ChooseableOffset]

По умолчанию в модели используется вейвлет, представленная wavenet объект, для выходной функции. The wavenet объект включает линейные и нелинейные компоненты.

Просмотрите Regressors свойство.

disp(sys.Regressors)
Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1 2]  [5 6 7]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

  Regressors described by this set

The idnlarx конструктор преобразует порядки модели в Regressors форма.

  • L- ags массив для y1, [1 2], эквивалентно na значение 2. Обе формы задают два последовательных выходных регрессора, y1(t-1) и y1(t-2).

  • The Lags массив для u1, [5 6 7], включает три задержки, указанные nb значение 3 и сдвигает их на nk значение 5. Поэтому входные регрессоры u1(t-5), u1(t-6), и u1(t-7).

Просмотрите регрессоры.

getreg(sys)
ans = 5×1 cell
    {'y1(t-1)'}
    {'y1(t-2)'}
    {'u1(t-5)'}
    {'u1(t-6)'}
    {'u1(t-7)'}

Можно использовать orders синтаксис для задания простых линейных регрессоров. Однако, чтобы создать более сложные регрессоры, используйте команды regressor linearRegressor, polynomialRegressor, и customRegressor чтобы создать комбинированный регрессор для Regressors синтаксис .

Открыть Live Script

Создайте idnlarx модель путем определения линейных регрессоров.

Создайте линейный регрессор, который содержит два выходных лага и два входных лага.

output_name = 'y1';
input_name = 'u1';
var_names = {output_name,input_name};

output_lag = [1 2];
input_lag = [1 2];
lags = {output_lag,input_lag};

reg = linearRegressor(var_names,lags)
reg = 
Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1 2]  [1 2]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

  Regressors described by this set

Модель содержит регрессоры y(t-1), y(t-2), u(t-1), и u(t-2).

Создайте idnlarx модели и просмотра регрессоров.

sys = idnlarx(output_name,input_name,reg);
getreg(sys)
ans = 4×1 cell
    {'y1(t-1)'}
    {'y1(t-2)'}
    {'u1(t-1)'}
    {'u1(t-2)'}

Просмотрите выходную функцию.

disp(sys.OutputFcn)
Wavelet Network

 Nonlinear Function: Wavelet network with number of units chosen automatically.
 Linear Function: uninitialized
 Output Offset: uninitialized

           Input: [1×1 idpack.Channel]
          Output: [1×1 idpack.Channel]
       LinearFcn: [1×1 nlident.internal.UseProjectedLinearFcn]
    NonlinearFcn: [1×1 nlident.internal.WavenetFcn]
          Offset: [1×1 nlident.internal.ChooseableOffset]

Просмотрите таблицу использования регрессора.

disp(sys.RegressorUsage)
               y1:LinearFcn    y1:NonlinearFcn
               ____________    _______________

    y1(t-1)       true              true      
    y1(t-2)       true              true      
    u1(t-1)       true              true      
    u1(t-2)       true              true

Все регрессоры являются входами как в линейный, так и в нелинейный компоненты wavenet объект.

Открыть Live Script

Создайте нелинейную модель ARX с линейным набором регрессоров.

Создайте линейный регрессор, который содержит три выходных лага и два входных лага.

output_name = 'y1';
input_name = 'u1';
var_names = {output_name,input_name};

output_lag = [1 2 3];
input_lag = [1 2];
lags = {output_lag,input_lag};

reg = linearRegressor(var_names,lags)
reg = 
Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1 2 3]  [1 2]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

  Regressors described by this set

Создайте нелинейную модель ARX.

sys = idnlarx(output_name,input_name,reg);

Просмотрите Regressors свойство.

disp(sys.Regressors)
Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1 2 3]  [1 2]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

  Regressors described by this set

sys использует wavenet как выходная функция по умолчанию. Перенастройте выходную функцию на sigmoidnet.

sys.OutputFcn = 'sigmoidnet';
disp(sys.OutputFcn)
Sigmoid Network

 Nonlinear Function: Sigmoid network with 10 units.
 Linear Function: uninitialized
 Output Offset: uninitialized

           Input: [1×1 idpack.Channel]
          Output: [1×1 idpack.Channel]
       LinearFcn: [1×1 nlident.internal.UseProjectedLinearFcn]
    NonlinearFcn: [1×1 nlident.internal.RidgenetFcn]
          Offset: [1×1 nlident.internal.ChooseableOffset]
Открыть Live Script

Задайте выходную функцию сигмоидной сети, когда вы создадите нелинейную модель ARX.

Присвойте имена переменных и укажите набор регрессоров.

output_name = 'y1';
input_name = 'u1';
r = linearRegressor({output_name,input_name},{1 1});

Создайте нелинейную модель ARX, которая задает sigmoidnet выходная функция. Установите количество членов в сигмоидном расширении на 15.

sys = idnlarx(output_name,input_name,r,sigmoidnet(15));

Просмотрите спецификацию выходной функции.

disp(sys.OutputFcn)
Sigmoid Network

 Nonlinear Function: Sigmoid network with 15 units.
 Linear Function: uninitialized
 Output Offset: uninitialized

           Input: [1×1 idpack.Channel]
          Output: [1×1 idpack.Channel]
       LinearFcn: [1×1 nlident.internal.UseProjectedLinearFcn]
    NonlinearFcn: [1×1 nlident.internal.RidgenetFcn]
          Offset: [1×1 nlident.internal.ChooseableOffset]
Открыть Live Script

Создайте idnlarx модель, которая использует только линейное отображение в выходной функции. Значение аргумента [] эквивалентно значению аргумента 'linear'.

sys = idnlarx([2 2 1],[])
sys = 
Nonlinear ARX model with 1 output and 1 input
  Inputs: u1
  Outputs: y1

Regressors:
  Linear regressors in variables y1, u1
  List of all regressors

Model output is linear in regressors.
Sample time: 1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.
Открыть Live Script

Создайте набор регрессоров, который включает линейные, полиномиальные и пользовательские регрессоры.

Задайте L как набор линейных регрессоров y1(t-1), u1(t-2), и u1(t-5).

L = linearRegressor({'y1','u1'},{1, [2 5]});

Задайте P как набор полиномиальных регрессоров y2(t-4)2, y2(t-5)2, y2(t-6)2, и y2(t-7)2.

P = polynomialRegressor('y2',4:7,2);

Задайте C как пользовательский регрессор sin(y1(t-1)u1(t-2)+u2(t-2)), с использованием @ символ для создания указателя анонимной функции.

C = customRegressor({'y1','u1','u2'},{1 2 2},@(x,y,z)sin(x.*y+z));

Объедините регрессоры в один набор регрессоров R.

R = [L;P;C]
R=3×1 object
[3 1] array of linearRegressor, polynomialRegressor, customRegressor objects.
------------------------------------
1. Linear regressors in variables y1, u1
       Variables: {'y1'  'u1'}
            Lags: {[1]  [2 5]}
     UseAbsolute: [0 0]
    TimeVariable: 't'

------------------------------------
2. Order 2 regressors in variables y2
               Order: 2
           Variables: {'y2'}
                Lags: {[4 5 6 7]}
         UseAbsolute: 0
    AllowVariableMix: 0
         AllowLagMix: 0
        TimeVariable: 't'

------------------------------------
3. Custom regressor: sin(y1(t-1).*u1(t-2)+u2(t-2))
    VariablesToRegressorFcn: @(x,y,z)sin(x.*y+z)
                  Variables: {'y1'  'u1'  'u2'}
                       Lags: {[1]  [2]  [2]}
                 Vectorized: 1
               TimeVariable: 't'

  Regressors described by this set

Создайте нелинейную модель ARX.

sys = idnlarx({'y1','y2'},{'u1','u2'},R)
sys = 
Nonlinear ARX model with 2 outputs and 2 inputs
  Inputs: u1, u2
  Outputs: y1, y2

Regressors:
  1. Linear regressors in variables y1, u1
  2. Order 2 regressors in variables y2
  3. Custom regressor: sin(y1(t-1).*u1(t-2)+u2(t-2))
  List of all regressors

Output functions:
  Output 1: Wavelet Network
  Output 2: Wavelet Network

Sample time: 1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.
Открыть Live Script

Используйте линейную модель ARX вместо набора регрессоров, чтобы создать нелинейную модель ARX.

Создайте линейную модель ARX с помощью idpoly.

A = [1 -1.2 0.5];
B = [0.8 1];
LinearModel = idpoly(A, B, 'Ts', 0.1);

Задайте имена входа и вывода для модели с помощью записи через точку.

LinearModel.OutputName = 'y1';
LinearModel.InputName = 'u1';

Создайте нелинейную модель ARX с помощью линейной модели ARX.

m1 = idnlarx(LinearModel)
m1 = 
Nonlinear ARX model with 1 output and 1 input
  Inputs: u1
  Outputs: y1

Regressors:
  Linear regressors in variables y1, u1
  List of all regressors

Output function: Wavelet Network

Sample time: 0.1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.

Можно создать линейную модель ARX из любой идентифицированной линейной модели дискретного времени.

Оцените модель пространства состояний второго порядка из данных оценки z1.

load iddata1 z1
ssModel = ssest(z1,2,'Ts',0.1);

Создайте нелинейную модель ARX из ssModel. Программа использует входные и выходные имена, которые ssModel извлекает из z1.

m2 = idnlarx(ssModel)
m2 = 
Nonlinear ARX model with 1 output and 1 input
  Inputs: u1
  Outputs: y1

Regressors:
  Linear regressors in variables y1, u1
  List of all regressors

Output function: Wavelet Network

Sample time: 0.1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.
Открыть Live Script

Измените назначения регрессора путем изменения RegressorUsage таблица.

Создайте нелинейную модель ARX, которая имеет два входа и два выхода.

Создайте имена переменных и регрессоры.

varnames = {'y1','y2','u1','u2'};
lags = {[1 2 3],[1 2],[1 2],[1 3]};
reg = linearRegressor(varnames,lags);

Создайте спецификацию выходной функции fcn который использует wavenet для отображения регрессоров в выходные y1 и sigmoidnet для отображения регрессоров в выходные y2. Оба объектов отображения содержат линейные и нелинейные компоненты.

fcn = [wavenet;sigmoidnet];

Создайте нелинейную модель ARX.

output_name = {'y1' 'y2'};
input_name = {'u1' 'u2'};
sys = idnlarx(output_name,input_name,reg,fcn)
sys = 
Nonlinear ARX model with 2 outputs and 2 inputs
  Inputs: u1, u2
  Outputs: y1, y2

Regressors:
  Linear regressors in variables y1, y2, u1, u2
  List of all regressors

Output functions:
  Output 1: Wavelet Network
  Output 2: Sigmoid Network with 10 units

Sample time: 1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.

Отобразите RegressorUsage таблица.

disp(sys.RegressorUsage)
               y1:LinearFcn    y1:NonlinearFcn    y2:LinearFcn    y2:NonlinearFcn
               ____________    _______________    ____________    _______________

    y1(t-1)       true              true             true              true      
    y1(t-2)       true              true             true              true      
    y1(t-3)       true              true             true              true      
    y2(t-1)       true              true             true              true      
    y2(t-2)       true              true             true              true      
    u1(t-1)       true              true             true              true      
    u1(t-2)       true              true             true              true      
    u2(t-1)       true              true             true              true      
    u2(t-3)       true              true             true              true

Строки таблицы представляют регрессоры. Первые два столбца таблицы представляют линейные и нелинейные компоненты отображения для вывода y1 (wavenet). Последние два столбца представляют два компонента отображения для вывода y2 (sigmoidnet).

В этой таблице все входной и выходной регрессоры являются входами ко всем компонентам.

Удалите y2(t-2) регрессор из y2 нелинейный компонент.

sys.RegressorUsage{4,4}=false;
disp(sys.RegressorUsage)
               y1:LinearFcn    y1:NonlinearFcn    y2:LinearFcn    y2:NonlinearFcn
               ____________    _______________    ____________    _______________

    y1(t-1)       true              true             true              true      
    y1(t-2)       true              true             true              true      
    y1(t-3)       true              true             true              true      
    y2(t-1)       true              true             true              false     
    y2(t-2)       true              true             true              true      
    u1(t-1)       true              true             true              true      
    u1(t-2)       true              true             true              true      
    u2(t-1)       true              true             true              true      
    u2(t-3)       true              true             true              true

В таблице отображаются false для этой пары регрессор-компонент.

Удалите все выходные регрессоры из y1 нелинейный компонент.

Store regressor names in Names.

Names = sys.RegressorUsage.Properties.RowNames;

Определите индексы строк, которые содержат y 1 или y 2 и установите соответствующие значения y1:NonlinearFcn на False.

idx = contains(Names,'y1')|contains(Names,'y2');
sys.RegressorUsage{idx,2} = false;
disp(sys.RegressorUsage)
               y1:LinearFcn    y1:NonlinearFcn    y2:LinearFcn    y2:NonlinearFcn
               ____________    _______________    ____________    _______________

    y1(t-1)       true              false            true              true      
    y1(t-2)       true              false            true              true      
    y1(t-3)       true              false            true              true      
    y2(t-1)       true              false            true              false     
    y2(t-2)       true              false            true              true      
    u1(t-1)       true              true             true              true      
    u1(t-2)       true              true             true              true      
    u2(t-1)       true              true             true              true      
    u2(t-3)       true              true             true              true

Значения таблицы отражают новые присвоения.

The RegressorUsage таблица обеспечивает полную гибкость для индивидуального управления назначениями регрессора.

Подробнее о

расширить все

Вопросы совместимости

расширить все

Не рекомендуемый запуск в R2021a

См. также

| | | | | | | | | |

Темы

Введенный в R2007a

Документация по System Identification Toolbox

Поддержка