Оцените модель пространства состояний с использованием данных временной области или частотного диапазона
sys = ssest(data,nx)sys порядка nx, использование данных data который может находиться в временном интервале или частотном диапазоне. sys является моделью следующей формы:
A, B, C, D, и K являются матрицами пространства состояний. u (t) - вход, y (t) - выход, e (t) - нарушение порядка, а x (t) - вектор nx состояния.
Все записи A, B, C и K по умолчанию являются свободно оцениваемыми параметрами. D по умолчанию фиксируется на нуле, что означает отсутствие сквозного соединения, кроме статических систем (nx = 0).
sys = ssest(data,nx,Name,Value)'Ts' аргумент пары "имя-значение". Используйте 'Form', 'Feedthrough', и 'DisturbanceModel' Аргументы пары "имя-значение" для изменения поведения по умолчанию матриц A, B, C, D и K.
Оцените модель пространства состояний и сравните ее ответ с измеренным выходом.
Загрузите входно-выходные данные, которые хранятся в iddata объект.
load iddata1 z1
Оцените модель пространства состояний четвертого порядка.
nx = 4; sys = ssest(z1,nx);
Сравните моделируемую характеристику модели с измеренным выходом.
compare(z1,sys)

График показывает, что процент соответствия между моделируемой моделью и данными оценки больше 70%.
Вы можете просмотреть больше информации об оценке, исследуя idss свойства sys.Report.
sys.Report
ans =
Status: 'Estimated using SSEST with prediction focus'
Method: 'SSEST'
InitialState: 'zero'
N4Weight: 'CVA'
N4Horizon: [6 10 10]
Fit: [1x1 struct]
Parameters: [1x1 struct]
OptionsUsed: [1x1 idoptions.ssest]
RandState: []
DataUsed: [1x1 struct]
Termination: [1x1 struct]
Для примера узнайте больше об условиях расторжения.
sys.Report.Termination
ans = struct with fields:
WhyStop: 'No improvement along the search direction with line search.'
Iterations: 7
FirstOrderOptimality: 85.9759
FcnCount: 123
UpdateNorm: 14.2002
LastImprovement: 0
Отчет включает информацию о количестве итераций и причине остановки итерации оценки.
Загрузите входно-выходные данные z1, который хранится в iddata объект. Это те же данные, что и для оценки модели четвертого порядка в модели пространства состояний.
load iddata1 z1
Определите оптимальный порядок модели путем определения аргумента nx как область значений от 1:10.
nx = 1:10; sys = ssest(z1,nx);
Автоматически сгенерированный график показывает сингулярные значения Ханкеля для моделей порядков, заданных nx.
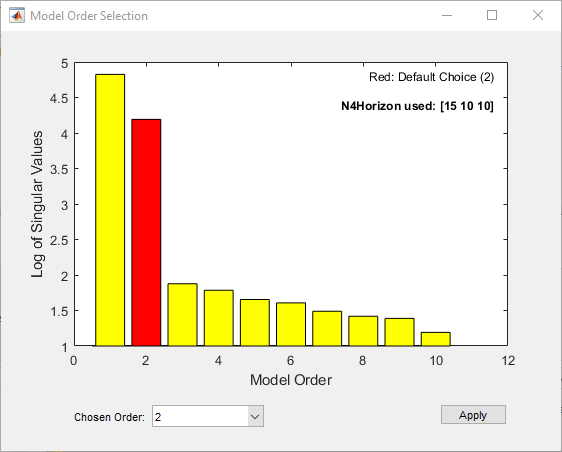
Состояния с относительно маленькими сингулярными значениями Ханкеля могут быть безопасно отброшены. Предлагаемый выбор порядка по умолчанию 2.
Выберите порядок модели в списке Chosen Order и нажмите Apply.
Загрузка данных отклика системы во временной области.
load iddata7 z7;
Идентифицируйте модель данных в пространстве состояний четвертого порядка. Задайте известную задержку 2 секунд для первого входа и 0 секунд для второго входа.
nx = 4;
sys = ssest(z7(1:300),nx,'InputDelay',[2;0]);Измените каноническую форму матриц A, B и C, включите исходный член в матрицу D и устраните оценку модели возмущения в матрице K.
Загрузите данные ввода-вывода и оцените систему четвертого порядка с помощью ssest опции по умолчанию.
load iddata1 z1 sys1 = ssest(z1,4);
Укажите сопутствующую форму и сравните A матрица с A по умолчанию матрица.
sys2 = ssest(z1,4,'Form','companion'); A1 = sys1.A
A1 = 4×4
-0.5155 -3.8483 0.6657 -0.2666
5.8665 -2.7285 1.0649 -1.4694
-0.4487 0.9308 -0.6235 18.8148
-0.4192 0.5595 -16.0688 0.5399
A2 = sys2.A
A2 = 4×4
103 ×
0 0 0 -7.1122
0.0010 0 0 -0.9547
0 0.0010 0 -0.3263
0 0 0.0010 -0.0033
Включите исходный термин и сравните D матрицы.
sys3 = ssest(z1,4,'Feedthrough',1);
D1 = sys1.DD1 = 0
D3 = sys3.D
D3 = 0.0339
Исключите моделирование нарушений порядка и сравните K матрицы.
sys4 = ssest(z1,4,'DisturbanceModel','none'); K1 = sys1.K
K1 = 4×1
0.0520
0.0973
0.0151
0.0270
K4 = sys4.K
K4 = 4×1
0
0
0
0
Задайте ssest оценить начальные состояния как параметры независимой оценки.
ssest может обрабатывать начальные состояния одним из нескольких методов. По умолчанию ssest автоматически выбирает метод на основе данных оценки. Вы можете самостоятельно выбрать метод, изменив набор опций с помощью ssestOptions.
Загрузите входно-выходные данные z1 и оцените модель пространства состояний второго порядка sys использование опций по умолчанию. Используйте синтаксис, который возвращает начальные состояния x0.
load iddata1 z1 [sys,x0] = ssest(z1,2); x0
x0 = 2×1
0
0
По умолчанию оценка выполняется с помощью 'auto' настройка для InitialState. Узнайте, какой метод ssest применяется путем рассмотрения значения InitialState в sys.Reporт.
sys.Report.InitialState
ans = 'zero'
Программное обеспечение применило 'zero' метод, означающий, что программное обеспечение устанавливает начальные состояния в нулевые, а не оценивает их. Этот выбор соответствует 0 значения, возвращенные для x0.
Задайте, что ssest оцените начальные состояния как независимые параметры, используя 'estimate' настройка. Использование ssestOptions чтобы создать измененный набор опций и задать этот набор опций для оценки новой модели.
opt = ssestOptions('InitialState','estimate'); [sys1,x0] = ssest(z1,2,opt); x0
x0 = 2×1
0.0068
0.0052
x0 теперь имеет оцененные параметры с ненулевыми значениями.
Получите регулярную модель пространства состояний пятого порядка для системы второго порядка из сигнала узкой полосы пропускания.
Данные оценки нагрузки.
load regularizationExampleData eData;
Создайте модель передаточной функции, используемую для генерации данных оценки (истинная система).
trueSys = idtf([0.02008 0.04017 0.02008],[1 -1.561 0.6414],1);
Оцените нерегулярную модель пространства состояний.
opt = ssestOptions('SearchMethod','lm'); m = ssest(eData,5,'form','modal','DisturbanceModel','none','Ts',eData.Ts,opt);
Оцените регуляризованную модель пространства состояний.
opt.Regularization.Lambda = 10; mr = ssest(eData,5,'form','modal','DisturbanceModel','none','Ts',eData.Ts,opt);
Сравните выходы модели с данными оценки.
compare(eData,m,mr);

Сравните импульсные характеристики модели.
impulse(trueSys,m,mr,50); legend('trueSys','m','mr');

Оцените модель пространства состояний измеренных входно-выходных данных. Сконфигурируйте ограничения параметров и начальные значения для оценки с помощью модели пространства состояний.
Создайте idss модель, чтобы задать начальную параметризацию для оценки.
A = blkdiag([-0.1 0.4; -0.4 -0.1],[-1 5; -5 -1]); B = [1; zeros(3,1)]; C = [1 1 1 1]; D = 0; K = zeros(4,1); x0 = [0.1 0.1 0.1 0.1]; Ts = 0; init_sys = idss(A,B,C,D,K,x0,Ts);
Установка всех записей K на 0 создает idss модель без элемента нарушения порядка состояния.
Используйте Structure свойство для фиксации значений некоторых параметров модели. Сконфигурируйте модель так, чтобы B и K являются фиксированными, и только ненулевые значения A могут быть оценены.
init_sys.Structure.A.Free = (A~=0); init_sys.Structure.B.Free = false; init_sys.Structure.K.Free = false;
Записи в init_sys.Structure.A.Free определить, соответствуют ли соответствующие записи в init_sys.A свободны (true) или фиксированный (false).
Загрузите измеренные данные и оцените модель пространства состояний с помощью ограничений параметра и начальных значений, заданных init_sys.
load iddata2 z2; sys = ssest(z2,init_sys);
Предполагаемые параметры sys удовлетворить ограничениям, заданным в init_sys.
data - Оценка данныхiddata | объекта frd | объекта idfrd объектОценочные данные, заданные как iddata объект, frd объект, или idfrd объект.
Для оценки во временной области, data должен быть iddata объект, содержащий значения входного и выходного сигналов.
Для оценки частотного диапазона, data может быть одним из следующих:
Данные оценки должны быть равномерно отобраны. По умолчанию программное обеспечение устанавливает шаг расчета модели на шаг расчета данных оценки.
Для мультиэксперентных данных шаги расчета и поведение интерсампов всех экспериментов должны совпадать.
Область данных определяет тип модели, которую вы можете оценить.
Данные частотного диапазона во временной области или в дискретном времени - модели непрерывного времени и дискретного времени
Непрерывные данные частотного диапазона - только модели непрерывного времени
nx - Порядок расчетной модели1:10 (по умолчанию) | положительный целочисленный скаляр | положительный целочисленный вектор | 0Порядок предполагаемой модели, заданный как неотрицательное целое число или как вектор, содержащий область значений положительных целых чисел.
Если вы уже знаете, какой порядок вы хотите, чтобы ваша предполагаемая модель имела, задайте nx как скаляр.
Если вы хотите сравнить область значений потенциальных порядков, чтобы выбрать наиболее эффективный порядок для вашей оценочной модели, задайте область значений в nx. ssest создает график Ханкеля с сингулярным значением, который показывает относительные энергетические вклады каждого состояния в системе. Состояния с относительно небольшими сингулярными значениями Ханкеля мало способствуют точности модели и могут быть отброшены с небольшим влиянием. Индекс самого высокого состояния, которое вы сохраняете, является порядком модели. Окно plot включает предложение для порядка на использование. Вы можете принять это предложение или ввести другой порядок. Для получения примера смотрите Определение Оптимального Предполагаемого Порядка Модели.
Если вы не задаете nx, или если вы задаете nx как bestпрограммное обеспечение автоматически выбирает nx из области значений 1:10.
Если вы идентифицируете статическую систему, установите nx на 0.
opt - опции оценкиssestOptions набор опцийОпции оценки, заданные как ssestOptions набор опций. Опции, заданные opt включают:
Цель оценки
Обработка начальных условий
Регуляризация
Численный метод поиска, используемый для оценки
Для примеров, показывающих, как использовать opt, см. Оценка начальных состояний как независимых параметров и оценка модели пространства состояний с использованием регуляризации.
init_sys - Линейная система, которая конфигурирует начальную параметризацию системыidss модель | линейная модель | структураЛинейная система, которая конфигурирует начальную параметризацию sys, заданный как idss модель или как структура. Получаете init_sys путем выполнения оценки с использованием измеренных данных или путем прямой конструкции.
Если init_sys является idss модель, ssest использует значения параметров init_sys как исходное предположение для оценки sys. Для получения информации о том, как задать idss, см. Оценка моделей пространства состояний со структурированной параметризацией. ssest учитывает ограничения, накладываемые на параметры init_sys, таких как фиксированные коэффициенты и минимальные/максимальные границы.
Используйте Structure свойство init_sys настроить начальные значения параметров и ограничения для A, B, C, D, и K матрицы. Для примера:
Чтобы задать начальное предположение для матрицы A init_sys, задать init_sys.Structure.A.Value как начальное предположение.
Чтобы задать ограничения для B матрицы init_sys:
Задайте init_sys.Structure.B.Minimum к минимальному значению матрицы B
Задайте init_sys.Structure.B.Maximum к максимальному B значению матрицы
Задайте init_sys.Structure.B.Free чтобы указать, являются ли записи матрицы B свободными параметрами для оценки
Чтобы задать более сложные ограничения, такие как взаимозависимость коэффициентов, используйте оценку в сером ящике с помощью greyest и idgrey.
Вы должны назначить конечные начальные значения для всех параметров матрицы.
Если init_sys не является пространством состояний (idss) модель, программное обеспечение сначала преобразует init_sys в idss модель. ssest использует параметры получившейся модели в качестве начального предположения для оценки.
Если вы не задаете opt и init_sys был получен путем оценки, затем программное обеспечение использует опции оценки из init_sys.Report.OptionsUsed.
Для получения примера смотрите Оценку частично известной модели пространства состояний с помощью структурированной оценки.
Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.
sys = ssest(data,nx,'Ts',0.1)'Ts' - Шаг расчета расчетной модели0 (непрерывное время) (по умолчанию) | время расчета данных (data.Ts) | положительная скалярная величинаШаги расчета предполагаемой модели, заданные как разделенная запятой пара, состоящие из 'Ts' и любой из них 0 или положительная скалярная величина.
Для моделей в непрерывном времени задайте 'Ts' как 0.
Для моделей в дискретном времени задайте 'Ts' как данные шаги расчета в модулях, хранящейся в TimeUnit свойство.
'InputDelay' - Входные задержки0
(по умолчанию) | скалярный вектор |Входная задержка для каждого входного канала, заданная как разделенная разделенными запятой парами, состоящая из 'InputDelay' и числовой вектор.
Для моделей в непрерывном времени задайте 'InputDelay' в модулях времени, сохраненных в TimeUnit свойство.
Для моделей в дискретном времени задайте 'InputDelay' в целочисленных множителях шага расчета Ts. Для примера установка 'InputDelay' на 3 задает задержку на три периода дискретизации.
Для системы с Nu входами установите InputDelay к Nu -by-1 вектору. Каждый элемент этого вектора является числовым значением, которое представляет входу задержку для соответствующего канала входа. Для получения примера смотрите Идентифицируйте модель пространства состояний с Входом задержкой.
Чтобы применить ту же задержку ко всем каналам, задайте InputDelay как скаляр.
'Form' - Тип канонической формы'free' (по умолчанию) | 'modal' | 'companion' | 'canonical'Тип канонической формы sys, заданная как разделенная разделенными запятой парами, состоящая из 'Form' и одно из следующих значений:
'free' - Все записи матриц A, B, C, D, и K рассматривают как свободные.
'modal' - Получение sys в модальной форме.
'companion' - Получение sys в сопутствующей форме.
'canonical' - Получение sys в канонической форме наблюдаемости.
Определения канонических форм см. в Canonical State-Space Realizations.
Для получения дополнительной информации см. «Оценка моделей пространства состояний с канонической параметризацией». Для получения примера см. раздел «Изменение форм, Сквозного соединения и Возмущения матриц».
'Feedthrough' - Прямое сквозное соединение от входа до выхода0 (по умолчанию) | 1 | логический векторПрямое сквозное соединение от входа до выхода, заданная как разделенная разделенными запятой парами, состоящая из 'Feedthrough' и логический вектор длины Nu, где Nu - количество входов. Если вы задаете Feedthrough в качестве логического скаляра это значение применяется ко всем входам. Для статических систем программное обеспечение всегда принимает 'Feedthrough' является 1.
Для получения примера см. раздел «Изменение форм, Сквозного соединения и Возмущения матриц».
'DisturbanceModel' - Опция для оценки параметров шумовой составляющей во временной области'estimate' (по умолчанию) | 'none'Опция для оценки параметров шумового компонента во временной области в матрице K, заданная как разделенная разделенными запятой парами, состоящая из 'DisturbanceModel' и одно из следующих значений:
'estimate' - Оцените компонент. Матрица K рассматривается как свободный параметр.
'none' - Не оценивать компонент. Элементы матрицы K зафиксированы в нуле.
Для данных частотного диапазона программное обеспечение принимает, что 'DisturbanceModel' является 'none'.
Для получения примера см. раздел «Изменение форм, Сквозного соединения и Возмущения матриц».
sys - Идентифицированная модель пространства состоянийidss модельИдентифицированная модель пространства состояний, возвращенная как idss модель. Эта модель создается с использованием заданных порядков модели, задержек и опций оценки.
Информация о результатах оценки и используемых опциях хранится в Report свойство модели. Report имеет следующие поля.
| Поле отчета | Описание | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Status | Сводными данными статуса модели, которое указывает, была ли модель создана конструкцией или получена оценкой. | ||||||||||||||||||
Method | Используется команда estimation. | ||||||||||||||||||
InitialState | Как исходные состояния обрабатывались во время оценки, возвращается как одно из следующих значений:
Это поле особенно полезно, когда | ||||||||||||||||||
N4Weight | Схема взвешивания, используемая для сингулярного разложения алгоритмом N4SID, возвращенная как одно из следующих значений:
Эта опция особенно полезна, когда | ||||||||||||||||||
N4Horizon | Прямой и обратный горизонты предсказания, используемые алгоритмом N4SID, возвращенные как вектор-строка с тремя элементами - | ||||||||||||||||||
Fit | Количественная оценка оценки, возвращенная как структура. Смотрите функции потерь и метрики качества модели для получения дополнительной информации об этих метриках качества. Структура имеет следующие поля:
| ||||||||||||||||||
Parameters | Оценочные значения параметров модели. | ||||||||||||||||||
OptionsUsed | Набор опций, используемый для оценки. Если пользовательские опции не были настроены, это набор опций по умолчанию. Посмотрите | ||||||||||||||||||
RandState | Состояние потока случайных чисел в начале оценки. Пустой, | ||||||||||||||||||
DataUsed | Атрибуты данных, используемых для оценки. Структурируйте следующие поля:
| ||||||||||||||||||
Termination | Условия завершения итерационного поиска, используемого для минимизации ошибки предсказания, возвращаются как структура со следующими полями:
Для методов оценки, которые не требуют численной оптимизации поиска, |
Для получения дополнительной информации об использовании Report, см. Отчет по оценке.
x0 - Начальные состояния, вычисленные во время оценкиНачальные состояния, вычисленные во время оценки, возвращаются как массив, содержащий вектор-столбец, соответствующий каждому эксперименту.
Этот массив также хранится в Parameters поле модели Report свойство.
Для получения примера смотрите Оценку начальных состояний как независимых Параметров.
ssest инициализирует оценки параметров с помощью или нетеративного подпространственного подхода, или итерационного подхода оценки рациональной функции. Затем он уточняет значения параметров, используя подход минимизации ошибок предсказания. Для получения дополнительной информации см. pem и ssestOptions.
[1] Ljung, L. System Identification: Теория для пользователя, Second Edition. Upper Saddle River, NJ: Prentice Hall PTR, 1999.
Поддержка параллельных вычислений доступна для оценки с помощью lsqnonlin метод поиска (требует Optimization Toolbox™). Чтобы включить параллельные вычисления, используйте ssestOptions, задать SearchMethod на 'lsqnonlin', и задать SearchOptions.Advanced.UseParallel на true.
Для примера:
opt = ssestOptions;
opt.SearchMethod = 'lsqnonlin';
opt.SearchOptions.Advanced.UseParallel = true;
canon | iddata | idfrd | idgrey | idss | n4sid | pem | polyest | procest | ssestOptions | ssregest | tfestУ вас есть измененная версия этого примера. Вы хотите открыть этот пример с вашими правками?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.