Нелинейные модели ARX можно оценить после выполнения следующих задач:
Подготовьте свои данные, как описано в Подготовке данных для нелинейной идентификации.
(Необязательно) Оцените заказы модели и задержки так же, как вы бы для линейных моделей ARX. См. Предварительный шаг - Оценка Порядков модели и Входа задержек.
(Необязательно) Выберите функцию отображения для выходной функции в Available Mapping Functions for Nonlinear ARX Models.
(Необязательно) Оцените или создайте линейную модель ARX для инициализации нелинейной модели ARX. См. «Инициализация нелинейной оценки ARX с помощью линейной модели».
nlarxИспользовать nlarx для создания и оценки нелинейной модели ARX. После каждой оценки проверяйте модель, сравнивая ее с другими моделями и моделируя или прогнозируя реакцию модели.
Базовая оценка
Начните с самой простой оценки, используя m = nlarx(data,[na nb nk]). Для примера:
load iddata1; % na = nb = 2 and nk = 1 m = nlarx(z1,[2 2 1])
m = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: Linear regressors in variables y1, u1 List of all regressors Output function: Wavelet Network with 1 unit Sample time: 0.1 seconds Status: Estimated using NLARX on time domain data "z1". Fit to estimation data: 68.83% (prediction focus) FPE: 1.975, MSE: 1.885
Просмотрите регрессоры.
getreg(m)
ans = 4×1 cell
{'y1(t-1)'}
{'y1(t-2)'}
{'u1(t-1)'}
{'u1(t-2)'}
Второй входной параметр [na nb nk] задает порядки модели и задержки. По умолчанию выходной функцией является вейвлет wavenet, который принимает регрессоры как входы в свои линейные и нелинейные функции. m является idnlarx объект.
Для систем MIMO, nb, nf, и nk ny -by - nu матрицы. См. nlarx страница с описанием для получения дополнительной информации об оценке MIMO.
Создайте nlarxOptions Опцию установите и сконфигурируйте Focus свойство для минимизации ошибки симуляции.
opt = nlarxOptions('Focus','simulation'); M = nlarx(z1,[2 2 1],'sigmoid',opt);
Линейные регрессоры
Линейные регрессоры представляют линейные функции, которые основаны на задержанных входных и выходных переменных и которые обеспечивают входы в выходную функцию модели. Когда вы используете порядки для задания модели, количество входа регрессоров равно na и количество выхода регрессоров равно nb. Синтаксис порядков ограничивает вас последовательными лагами. Можно также создать линейные регрессоры с помощью linearRegressor. Когда вы используете linearRegressor, можно задать произвольные лаги.
Полиномиальные регрессоры
Исследуйте включение полиномиальных регрессоров с помощью polynomialRegressor в дополнение к линейным регрессорам в нелинейной структуре модели ARX. Полиномиальные регрессоры являются полиномиальными функциями задержанных входов и выходов. (см. «Нелинейные порядки модели ARX и задержка»).
Для примера сгенерируйте полиномиальные регрессоры до порядка 2.
P = polynomialRegressor({'y1','u1'},{[1],[2]},2);Добавьте полиномиальные регрессоры к линейным регрессорам в m.Regressors.
m.Regressors = [m.Regressors;P]; getreg(m)
ans = 8×1 cell
{'y1(t-1)' }
{'y1(t-2)' }
{'u1(t-1)' }
{'u1(t-2)' }
{'y1(t-3)' }
{'y1(t-5)' }
{'y1(t-1)^2'}
{'u1(t-2)^2'}
m теперь включает полиномиальные регрессоры.
Просмотрите размер m.Regressors массив.
size(m.Regressors)
ans = 1×2
3 1
Массив теперь содержит три объекта регрессора.
Настраиваемые регрессоры
Использование customRegressor создать регрессоры как произвольные функции входных и выходных переменных модели.
.Для примера создайте два пользовательских регрессора, которые реализуют 'sin(y1(t-1)' и 'y1(t-2).*u1(t-3)'.
C1 = customRegressor({'y1'},{1},@(x)sin(x));
C2 = customRegressor({'y1','u1'},{2,3},@(x,y)x.*y);
m.Regressors = [m.Regressors;C1;C2];
getreg(m) % displays all regressorsans = 10×1 cell
{'y1(t-1)' }
{'y1(t-2)' }
{'u1(t-1)' }
{'u1(t-2)' }
{'y1(t-3)' }
{'y1(t-5)' }
{'y1(t-1)^2' }
{'u1(t-2)^2' }
{'sin(y1(t-1))' }
{'y1(t-2).*u1(t-3)'}
Просмотрите свойства пользовательских регрессоров. Например, получите указатель на функцию первого пользовательского регрессора в массиве. Этот регрессор является четвертым регрессором, установленным в Regressors массив.
C1_fcn = m.Regressors(4).VariablesToRegressorFcn
C1_fcn = function_handle with value:
@(x)sin(x)
Просмотрите описание регрессора.
display(m.Regressors(4))
Custom regressor: sin(y1(t-1))
VariablesToRegressorFcn: @(x)sin(x)
Variables: {'y1'}
Lags: {[1]}
Vectorized: 1
TimeVariable: 't'
Regressors described by this set
Объедините регрессоры
Как только вы создали линейные, полиномиальные и пользовательские объекты регрессора, можно объединить их любым способом, которым вы хотите удовлетворить ваши потребности в оценке.
Регрессоры модели могут вводить в качестве входов один или оба линейных и нелинейных функциональных компонентов функций отображения, составляющих выходную функцию. Чтобы уменьшить сложность модели и сохранить оценку хорошо обусловленной, рассмотрите назначение уменьшенного набора регрессоров нелинейному компоненту. Линейному компоненту можно также назначить подмножество регрессоров. Таблица использования регрессора, которая управляет назначениями, обеспечивает полную гибкость. Каждому компоненту можно назначить любую комбинацию регрессоров. Для примера задайте нелинейную модель ARX, которая будет линейной в прошлых выходах и нелинейной в прошлых входах.
m = nlarx(z1,[2 2 1]); disp(m.RegressorUsage)
y1:LinearFcn y1:NonlinearFcn
____________ _______________
y1(t-1) true true
y1(t-2) true true
u1(t-1) true true
u1(t-2) true true
m.RegressorUsage{3:4,1} = false;
m.RegressorUsage{1:2,2} = false;
disp(m.RegressorUsage) y1:LinearFcn y1:NonlinearFcn
____________ _______________
y1(t-1) true false
y1(t-2) true false
u1(t-1) false true
u1(t-2) false true
В следующей таблице представлены доступные объекты отображения для выходной функции модели.
| Описание отображения | Значение (объект сопоставления по умолчанию Строение) | Объект отображения |
|---|---|---|
| Вейвлет (по умолчанию) | 'wavenet' или 'wave' | wavenet |
| Один слой сигмоидная сеть | 'sigmoidnet' или 'sigm' | sigmoidnet |
| Древовидный раздел | 'treepartition' или 'tree' | treepartition |
| F линейна в x | 'linear' или [ ] или '' | linear |
Дополнительные доступные объекты отображения включают многослойные нейронные сети и пользовательские сети, которые вы создаете.
Задайте многослойную нейронную сеть, используя:
m = nlarx(data,[na nb nk],NNet)
где NNet - объект нейронной сети, созданный вами с помощью программного обеспечения Deep Learning Toolbox™. См. neuralnet страница с описанием.
Задайте пользовательскую сеть путем определения функции, вызываемой gaussunit.m, как описано в customnet страница с описанием. Определите пользовательский сетевой объект CNetw и оцените модель:
CNetw = customnet(@gaussunit); m = nlarx(data,[na nb nk],CNetw)
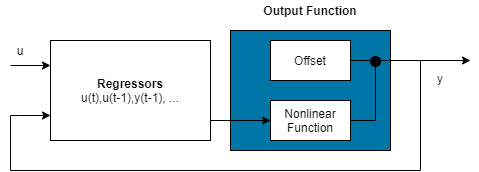
Если ваша выходная функция модели включает wavenet, sigmoidnet, или customnet отображая объекты, можно исключить линейную функцию с помощью LinearFcn.Use свойство объекта отображения. Объект отображения становится F (x) =, где g (.) - нелинейная функция, и y 0 является смещением.
Примечание
Вы не можете исключить линейную функцию из объектов древовидного разбиения и отображения нейронной сети.
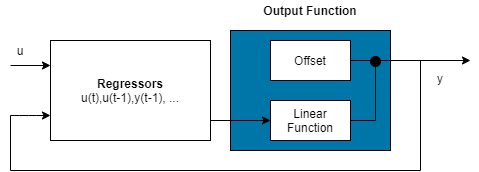
Сконфигурируйте нелинейную структуру ARX, чтобы включить только линейную функцию в объект отображения путем установки объекта отображения на linear. В этом случае, является взвешенной суммой регрессоров модели плюс смещение. Такие модели обеспечивают мост между чисто линейными моделями ARX и полностью гибкими нелинейными моделями.
Популярное нелинейное строение ARX во многих приложениях использует полиномиальные регрессоры, чтобы смоделировать нелинейности системы. В таких случаях система рассматривается как линейная комбинация производных (отложенных) входных и выходных переменных. Используйте polynomialRegressor команда для легкой генерации комбинаций продуктов и степеней.
Например, предположите, что Вы знаете, что выход y (<reservedrangesplaceholder2>) системы линейная комбинация (y (t − 1))2, (u (t − 1))2 и y (t − 1) u (t − 1)). Чтобы смоделировать такую систему, используйте:
P = polynomialRegressor({'y1','u1'},{1,1},2)P =
Order 2 regressors in variables y1, u1
Order: 2
Variables: {'y1' 'u1'}
Lags: {[1] [1]}
UseAbsolute: [0 0]
AllowVariableMix: 0
AllowLagMix: 0
TimeVariable: 't'
Regressors described by this set
P.AllowVariableMix = true;
M = nlarx(z1,P,'linear');
getreg(M)ans = 3×1 cell
{'y1(t-1)^2' }
{'u1(t-1)^2' }
{'y1(t-1)*u1(t-1)'}
Для более сложных комбинаций полиномиальных задержек и регрессоров со смешанными переменными можно также использовать customRegressor.
Если ваша структура модели включает объекты отображения, которые поддерживают итерационный поиск (см., Задайте опции оценки для нелинейных моделей ARX), можно использовать nlarx для уточнения параметров модели:
m1 = nlarx(z1,[2 2 1],'sigmoidnet'); m2 = nlarx(z1,m1); % can repeatedly run this command
Можно также использовать pem для уточнения исходной модели:
m2 = pem(z1,m1);
Проверьте критерий завершения поиска m.Report.Termination.WhyStop . Если WhyStop указывает, что оценка достигла максимального количества итераций, попробуйте повторить оценку и, возможно, указать большее значение для nlarxOptions.SearchOptions.MaxIterations опция оценки:
opt = nlarxOptions; opt.SearchOptions.MaxIterations = 30; m2 = nlarx(z1,m1,opt); % runs 30 more iterations % starting from m1
Когда m.Report.Termination.WhyStop значение Near (local) minimum, (norm( g) < tol или No improvement along the search direction with line search , проверьте свою модель, чтобы увидеть, соответствует ли эта модель данным. Если нет, решение может застрять в локальном минимуме поверхности функции затрат. Попробуйте настроить SearchOptions .Tolerance значение или SearchMethod опция в наборе опций nlarxOptions и повторите оценку.
Можно также попробовать возмущать параметры последней модели, используя init (называемая рандомизацией) и уточнение модели с помощью nlarx:
M1 = nlarx(z1, [2 2 1], 'sigmoidnet'); % original model M1p = init(M1); % randomly perturbs parameters about nominal values M2 = nlarx(z1, M1p); % estimates parameters of perturbed model
Прогресс итерационного поиска можно отобразить в Командном Окне MATLAB с помощью nlarxOptions.Display опция оценки:
opt = nlarxOptions('Display','on'); M2= nlarx(z1,M1p,opt);
Если вы не получите удовлетворительную модель после многих испытаний с различными структурами модели и настройками алгоритма, возможно, что данные плохие. Например, ваши данные могут отсутствовать важные входные или выходные переменные и недостаточно охватывают все рабочие точки системы.
Нелинейная черно-коробочная система идентификации обычно требует больше данных, чем линейная идентификация модели, чтобы получить достаточную информацию о системе.
В этом примере показано, как использовать nlarx для оценки нелинейной модели ARX для измеренных входных/выходных данных.
Подготовим данные к оценке.
load twotankdata
z = iddata(y, u, 0.2);
ze = z(1:1000); zv = z(1001:3000);Оцените несколько моделей, используя различные порядки моделей, задержки и настройки нелинейности.
m1 = nlarx(ze,[2 2 1]); m2 = nlarx(ze,[2 2 3]); m3 = nlarx(ze,[2 2 3],wavenet(8));
Альтернативный способ выполнить оценку - сначала сконфигурировать структуру модели, а затем оценить эту модель.
m4 = idnlarx([2 2 3],sigmoidnet(14));
m4.RegressorUsage.("y1:NonlinearFcn")(3:4) = false;
m4 = nlarx(ze,m4);Сравните получившиеся модели путем построения графиков выходов модели с измеренным выходом.
compare(zv, m1,m2,m3,m4)
