Нелинейные модели ARX расширяют линейную модель ARX до нелинейного случая. Для получения информации о структуре нелинейных моделей ARX, смотрите Что такое нелинейные модели ARX?
Вы можете оценить нелинейные модели ARX в приложении System Identification или в командной строке, используя nlarx команда. Чтобы оценить нелинейную модель ARX, вы сначала подготовите данные оценки. Затем вы конфигурируете структуру модели и алгоритм оценки, а затем выполняете оценку. После оценки можно подтвердить предполагаемую модель, как описано в Validate Nonlinear ARX Models.
Можно использовать равномерно дискретизированные входно-выходные данные временной области или данные timeseries (без входов) для оценки нелинейных моделей ARX. Ваши данные могут иметь нуль или более входных каналов и один или несколько выходных каналов. Вы не можете использовать данные частотного диапазона для оценки.
Чтобы подготовить данные к оценке модели, импортируйте ваши данные в MATLAB® Рабочая область и выполните одно из следующих действий:
В приложении Системы идентификации - Импортируйте данные в приложение, как описано в Представительных данных.
В командной строке - Представьте свои данные как iddata объект.
После импорта данных можно проанализировать качество данных и обработать данные путем интерполяции отсутствующих значений, фильтрации для выделения определенной частотной области значений или повторной дискретизации с использованием другого шага расчета. Для получения дополнительной информации см. Способы подготовки данных к системе идентификации. Для большинства приложений вам не нужно удалять смещения и линейные тренды из данных перед нелинейным моделированием. Однако удаление тренда данных может быть полезно в некоторых случаях, таких как перед моделированием зависимости между изменением входного и выходного входов относительно рабочей точки.
После подготовки данных оценки можно сконфигурировать структуру модели, функцию потерь и алгоритм оценки, а затем оценить модель с помощью данных оценки.
Нелинейная модель ARX состоит из набора регрессоров, которые могут быть любой комбинацией линейных, полиномиальных и пользовательских регрессоров, и выходной функции, которая обычно содержит нелинейные и линейные компоненты, а также статическое смещение. Схема блока представляет структуру нелинейной модели ARX в сценарии симуляции.
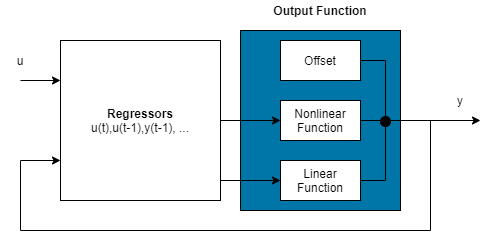
Чтобы сконфигурировать структуру нелинейной модели ARX:
Сконфигурируйте регрессоры модели.
Выберите линейные, полиномиальные и пользовательские регрессоры на основе ваших знаний о физической системе, которую вы пытаетесь смоделировать.
Задайте linear regressors одним из следующих способов:
Задайте порядки модели и задержку, чтобы создать набор линейных регрессоров. Для получения дополнительной информации см. «Нелинейные порядки модели ARX» и «Задержка».
Непосредственно задайте линейные регрессоры путем построения и использования linearRegressor объекты.
Инициализируйте модель с помощью линейной модели ARX. Выполнить эту операцию можно только в командной строке. Инициализация конфигурирует нелинейную модель ARX, чтобы использовать линейные регрессоры линейной модели. Для получения дополнительной информации см. «Инициализация нелинейной оценки ARX с помощью линейной модели».
Задайте polynomial regressors и custom regressors. Полиномиальные регрессоры являются полиномами, которые состоят из задержанных входных и выходных переменных. Пользовательские регрессоры являются произвольными функциями прошлых входов и выходов, такие как продукты, степени и другие выражения MATLAB входных и выходных переменных. Задайте полиномиальные и пользовательские регрессоры в дополнение к линейным регрессорам или вместо них для большей гибкости в моделировании ваших данных. Для получения дополнительной информации смотрите polynomialRegressor и customRegressor.
Назначьте регрессоры в качестве входов линейным и нелинейным компонентам блока выходной функции. Любой регрессор может быть назначен любому из этих компонентов или обоим. Ограничение количества регрессоров, которые являются входными для нелинейного компонента, может помочь уменьшить сложность модели и сохранить оценку хорошо обусловленной.
Выбор регрессоров для использования в каждом компоненте может потребовать нескольких испытаний. Можно изучить нелинейный график ARX, чтобы помочь вам получить представление о том, какие регрессоры наиболее сильно влияют на выход модели. Понимание относительной важности регрессоров на выходе может помочь вам решить, как назначить регрессоры.
Сконфигурируйте блок выходной функции.
Задайте и сконфигурируйте выходную функцию F (x).
Здесь x является вектором регрессоров, и r является средним значением x регрессоров. - выход блока линейной функции. представляет выход нелинейного функционального блока. Q - проекционная матрица, которая делает вычисления хорошо обусловленными. d является скалярным смещением, которое добавляется к комбинированным выходам линейного и нелинейного блоков. Точная форма F (x) зависит от вашего выбора выходной функции. Можно выбрать из доступных оценок нелинейности, таких как сети древовидного разбиения, вейвлет и многослойные нейронные сети. Можно также исключить из выходной функции линейный или нелинейный функциональный блок.
Можно также выполнить одну из следующих задач:
Исключить нелинейную функцию из выходной функции таким образом, чтобы F (x) =.
Исключить линейную функцию из выходной функции таким образом, чтобы F (x) =.
Примечание
Вы не можете исключить линейную функцию из древовидных разделов и нейронных сетей.
Для получения информации о том, как сконфигурировать структуру модели в командной строке и в приложении, смотрите Оценка нелинейных моделей ARX в командной строке и Оценка нелинейных моделей ARX в приложении.
Чтобы сконфигурировать оценку модели, задайте функцию потерь, которая будет минимизирована, и выберите алгоритм оценки и другие опции оценки, чтобы выполнить минимизацию.
Функция потерь или функция затрат является функцией ошибки между выходом модели и измеренным выходом. Для получения дополнительной информации о функциях потерь смотрите Loss Function и Model Quality Metrics.
В командной строке используйте nlarx набор опций, nlarxOptions чтобы сконфигурировать функцию потерь. Можно задать следующие опции:
Focus - Определяет, минимизируется ли ошибка симуляции или предсказания во время оценки параметра. По умолчанию программа минимизирует одношаговые ошибки предсказания, которые соответствуют Focus значение 'prediction'. Если вы хотите модель, которая оптимизирована для воспроизведения поведения симуляции, задайте Focus как 'simulation'. Минимизация ошибки симуляции требует дифференцируемых нелинейных функций и занимает больше времени, чем минимизация ошибки предсказания на один шаг вперед. Таким образом, вы не можете использовать treepartition и neuralnet нелинейности при минимизации ошибки симуляции, потому что эти оценки нелинейности не дифференцируемы.
OutputWeight - Задает взвешивание ошибки в многозначных оценках.
Regularization - Изменяет функцию потерь, чтобы добавить штраф от отклонения расчетных параметров. Для получения дополнительной информации см. «Регуляризованные оценки параметров модели».
Чтобы оценить нелинейную модель ARX, программа использует итерационные алгоритмы поиска, чтобы минимизировать ошибку между выходом моделируемой или предсказанной модели и измеренным выходом. В командной строке используйте nlarxOptions для определения алгоритма поиска и других опций оценки. Можно задать следующие опции:
SearchMethod - Метод поиска для минимизации ошибок предсказания или симуляции, таких как поиск линий Гаусса-Ньютона и Левенберга-Марквардта и подход Доверительной области-Отражающего Ньютона.
SearchOptions - Набор опций для алгоритма поиска с полями, которые зависят от значения SearchMethod, таких как:
MaxIterations - Максимальное количество итераций.
Tolerance - Условие завершения итерационного поиска, когда ожидаемое улучшение значений параметров меньше заданного значения.
Чтобы увидеть полный список доступных опций оценки, см. nlarxOptions. Для получения дополнительной информации о том, как задать эти опции оценки в приложении, смотрите Оценку нелинейных моделей ARX в Приложении.
После предварительной обработки данных оценки и конфигурирования структуры модели и опций оценки можно оценить модель в приложении System Identification или используя nlarx в командной строке. Получившаяся модель является idnlarx объект, который хранит все данные модели, включая регрессоры модели и параметры оценщика нелинейности. Для получения дополнительной информации об этих объектах модели см. «Нелинейные структуры модели». Можно подтвердить предполагаемую модель, как описано в Валидация нелинейных моделей ARX.
В командной строке можно использовать полиномиальную модель структуры ARX (idpoly с только A и B как активные полиномы) для нелинейной оценки ARX. Чтобы узнать больше о том, когда использовать линейные модели, см. Раздел «Когда подгонять нелинейные модели».
Обычно вы создаете линейную модель ARX с помощью arx команда. Можно предоставить линейную модель при построении или оценке нелинейной модели ARX. Для примера используйте следующий синтаксис, чтобы оценить нелинейную модель ARX с помощью данных оценки и линейной модели ARX LinARXModel.
m = nlarx(data,LinARXModel)
Вот m является idnlarx объект, и data является временной областью iddata объект. Программа использует линейную модель для инициализации нелинейной оценки ARX путем:
Присвоение порядков и задержек линейной модели ARX в качестве начальных значений заказов нелинейной модели ARX (na и nb свойствами idnlarx объект) и задержки (nk свойство). Программа использует эти порядки и задержки, чтобы вычислить линейные регрессоры в нелинейной структуре модели ARX.
Использование полиномов A и B линейной модели для вычисления линейной функции вычислителей нелинейности (LinearCoef параметр объекта оценки нелинейности), за исключением того, что блок оценки нелинейности является нейронной сетью.
Во время оценки алгоритм оценки использует эти значения, чтобы настроить нелинейную модель к данным.
Примечание
Когда вы используете те же данные для оценки, нелинейная модель ARX, инициализированная с помощью линейной модели ARX, производит лучшую подгонку к измеренному выходу, чем сама линейная модель ARX.
По умолчанию оценщиком нелинейности является вейвлет (wavenet объект). Можно также задать различные входные и выходные оценки нелинейности. Для примера можно задать оценщик нелинейности сигмоидной сети.
m = nlarx(data,LinARXModel,'sigmoid')Для получения примера смотрите Оценку нелинейных моделей ARX, инициализированных с использованием линейных моделей ARX.