Оценка параметров нелинейной модели ARX
sys = nlarx(data,orders)
sys = nlarx(data,regressors)regressors. Используйте этот синтаксис, когда у вас есть линейные регрессоры, которые имеют непоследовательные лаги, или когда у вас также есть полиномиальные регрессоры, пользовательские регрессоры или оба.
sys = nlarx(___,output_fcn)
sys = nlarx(data,linmodel,output_fcn)
sys = nlarx(data,sys0)sys0.
Используйте этот синтаксис для:
Оцените параметры модели, ранее созданной с помощью idnlarx конструктор. До оценки можно сконфигурировать свойства модели с помощью записи через точку.
Обновите параметры ранее оцененной модели, чтобы улучшить подгонку к данным оценки. В этом случае алгоритм оценки использует параметры sys0 как исходные догадки.
Загрузите данные оценки.
load twotankdata;Создайте iddata объект из данных оценки со шаг расчета 0,2 секунды.
Ts = 0.2; z = iddata(y,u,Ts);
Оцените нелинейную модель ARX с помощью порядков модели ARX, чтобы задать регрессоры.
sysNL = nlarx(z,[4 4 1])
sysNL = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: Linear regressors in variables y1, u1 List of all regressors Output function: Wavelet Network with 11 units Sample time: 0.2 seconds Status: Estimated using NLARX on time domain data "z". Fit to estimation data: 96.84% (prediction focus) FPE: 3.482e-05, MSE: 3.431e-05
sys использует значение по умолчанию wavenet функция как выходная функция.
Для сравнения вычислите линейную модель ARX с теми же порядками моделей.
sysL = arx(z,[4 4 1]);
Сравните выходы модели с исходными данными.
compare(z,sysNL,sysL)

Нелинейная модель намного лучше соответствует данным, чем линейная модель.
Задайте линейный регрессор, который эквивалентен матрице порядка ARX-модели [4 4 1].
Матрица порядка [4 4 1] указывает, что и входной, и выход наборы регрессоров содержат четыре регрессора с лагами в диапазоне от 1 до 4. Для примера, представляет второй входной регрессор.
Задайте выходные и входные имена.
output_name = 'y1'; input_name = 'u1'; names = {output_name,input_name};
Задайте выходные и входные лаги.
output_lag = [1 2 3 4];
input_lag = [1 2 3 4];
lags = {output_lag,input_lag};Создайте объект линейного регрессора.
lreg = linearRegressor(names,lags)
lreg =
Linear regressors in variables y1, u1
Variables: {'y1' 'u1'}
Lags: {[1 2 3 4] [1 2 3 4]}
UseAbsolute: [0 0]
TimeVariable: 't'
Regressors described by this set
Загрузите данные оценки и создайте объект iddata.
load twotankdata
z = iddata(y,u,0.2);Оцените нелинейную модель ARX.
sys = nlarx(z,lreg)
sys = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: Linear regressors in variables y1, u1 List of all regressors Output function: Wavelet Network with 11 units Sample time: 0.2 seconds Status: Estimated using NLARX on time domain data "z". Fit to estimation data: 96.84% (prediction focus) FPE: 3.482e-05, MSE: 3.431e-05
Просмотр регрессоров
getreg(sys)
ans = 8×1 cell
{'y1(t-1)'}
{'y1(t-2)'}
{'y1(t-3)'}
{'y1(t-4)'}
{'u1(t-1)'}
{'u1(t-2)'}
{'u1(t-3)'}
{'u1(t-4)'}
Сравните выход модели с данными оценки.
compare(z,sys)

Создайте время и массивы данных.
dt = 0.01; t = 0:dt:10; y = 10*sin(2*pi*t)+rand(size(t));
Создайте iddata объект без заданного входного сигнала.
z = iddata(y',[],dt);
Оцените нелинейную модель ARX.
sys = nlarx(z,2)
sys = Nonlinear time series model Outputs: y1 Regressors: Linear regressors in variables y1 List of all regressors Output function: Wavelet Network with 8 units Sample time: 0.01 seconds Status: Estimated using NLARX on time domain data "z". Fit to estimation data: 92.92% (prediction focus) FPE: 0.2568, MSE: 0.2507
Оцените нелинейную модель ARX, которая использует функцию отображения sigmoidnet как свою выходную функцию.
Загрузите данные и разделите их на наборы данных оценки и валидации ze и zv.
load twotankdata.mat u y z = iddata(y,u,'Ts',0.2); ze = z(1:1500); zv = z(1501:end);
Сконфигурируйте sigmoidnet функция отображения. Установите смещение равным 0,2, а количество модулей - 15.
s = sigmoidnet; s.Offset.Value = 0.2; s. NonlinearFcn.NumberOfUnits = 15;
Создайте линейную модель спецификации регрессора, которая содержит четыре выходных регрессора и пять входных регрессоров.
reg1 = linearRegressor({'y1','u1'},{1:4,0:4});Создайте спецификацию регрессора полиномиальной модели, которая содержит квадраты двух входных членов и трех выходных членов.
reg2 = polynomialRegressor({'y1','u1'},{1:2,0:2},2);Установите опции оценки для метода поиска и максимального количества итераций.
opt = nlarxOptions('SearchMethod','fmincon')'; opt.SearchOptions.MaxIterations = 40;
Оцените нелинейную модель ARX.
sys = nlarx(ze,[reg1;reg2],s,opt);
Валидация sys путем сравнения моделируемой характеристики модели с набором данных валидации.
compare(zv,sys)

Оцените линейную модель и улучшите модель путем добавления treepartition выходная функция.
Загрузите данные оценки.
load throttledata ThrottleData
Оцените линейную модель ARX linsys с порядками [2 2 1].
linsys = arx(ThrottleData,[2 2 1]);
Создайте idnlarx модель шаблона, которая использует linsys и определяет sigmoidnet как выходная функция.
sys0 = idnlarx(linsys,treepartition);
Исправьте линейный компонент sys0 так, что во время оценки линейный фрагмент sys0 остается идентичным linsys.
sys0.OutputFcn.LinearFcn.Free = false;
Оцените свободные параметры sys0, которые являются параметрами нелинейной функции и смещением.
sys = nlarx(ThrottleData,sys0);
Сравните точности аппроксимации для линейной и нелинейной моделей.
compare(ThrottleData,linsys,sys)

Для генерации пользовательского объекта отображения сетей требуется определение пользовательской единичной функции.
Определите функцию модуля и сохраните ее как gaussunit.m.
% Copyright 2015 The MathWorks, Inc. function [f, g, a] = gaussunit(x) f = exp(-x.*x); if nargout>1 g = -2*x.*f; a = 0.2; end
Создайте пользовательский объект сопоставления сетей с помощью указателя на gaussunit функция.
H = @gaussunit; CNet = customnet(H);
Загрузите данные оценки.
load iddata1;
Оцените нелинейную модель ARX с помощью пользовательской сети.
sys = nlarx(z1,[1 2 1],CNet)
sys = <strong>Nonlinear ARX model with 1 output and 1 input</strong> Inputs: u1 Outputs: y1 Regressors: Linear regressors in variables y1, u1 Output function: Custom Network with 10 units Sample time: 0.1 seconds Status: Estimated using NLARX on time domain data "z1". Fit to estimation data: 64.35% (prediction focus) FPE: 3.58, MSE: 2.465
Загрузите данные оценки.
load motorizedcamera;Создайте iddata объект.
z = iddata(y,u,0.02,'Name','Motorized Camera','TimeUnit','s');
z является iddata объект с шестью входами и двумя выходами.
Задайте порядки моделей.
Orders = [ones(2,2),2*ones(2,6),ones(2,6)];
Задайте различные функции отображения для каждого выходного канала.
NL = [wavenet('NumberOfUnits',2),linear];Оцените нелинейную модель ARX.
sys = nlarx(z,Orders,NL)
sys = Nonlinear ARX model with 2 outputs and 6 inputs Inputs: u1, u2, u3, u4, u5, u6 Outputs: y1, y2 Regressors: Linear regressors in variables y1, y2, u1, u2, u3, u4, u5, u6 List of all regressors Output functions: Output 1: Wavelet Network with 2 units Output 2: Linear Function Sample time: 0.02 seconds Status: Estimated using NLARX on time domain data "Motorized Camera". Fit to estimation data: [98.72;98.77]% (prediction focus) FPE: 0.5719, MSE: 1.061
Загрузите данные оценки и создайте iddata z объекта. z содержит два выходных канала и шесть входных каналов.
load motorizedcamera;
z = iddata(y,u,0.02);Задайте набор линейных регрессоров, которые используют выходные и входные имена от z и содержит:
2 выходных регрессора с 1 задержкой.
6 входных пар регрессора с 1 и 2 лагами.
names = [z.OutputName; z.InputName];
lags = {1,1,[1,2],[1,2],[1,2],[1,2],[1,2],[1,2]};
reg = linearRegressor(names,lags);Оцените нелинейную модель ARX с помощью sigmoidnet функция отображения с четырьмя модулями для всех выходных каналов.
sys = nlarx(z,reg,sigmoidnet(4))
sys = Nonlinear ARX model with 2 outputs and 6 inputs Inputs: u1, u2, u3, u4, u5, u6 Outputs: y1, y2 Regressors: Linear regressors in variables y1, y2, u1, u2, u3, u4, u5, u6 List of all regressors Output functions: Output 1: Sigmoid Network with 4 units Output 2: Sigmoid Network with 4 units Sample time: 0.02 seconds Status: Estimated using NLARX on time domain data "z". Fit to estimation data: [98.86;98.79]% (prediction focus) FPE: 2.641, MSE: 0.9233
Загрузите данные оценки z1, который имеет один вход и один выход, и получают выходные и входные имена.
load iddata1 z1; names = [z1.OutputName z1.InputName]
names = 1×2 cell
{'y1'} {'u1'}
Задайте L как набор линейных регрессоров, который представляет , , и .
L = linearRegressor(names,{1,[2 5]});Задайте P как полиномиальный регрессор .
P = polynomialRegressor(names(1),1,2);
Задайте C как пользовательский регрессор . Используйте указатель анонимной функции, чтобы задать эту функцию.
C = customRegressor(names,{2 3},@(x,y)x.*y)C =
Custom regressor: y1(t-2).*u1(t-3)
VariablesToRegressorFcn: @(x,y)x.*y
Variables: {'y1' 'u1'}
Lags: {[2] [3]}
Vectorized: 1
TimeVariable: 't'
Regressors described by this set
Объедините регрессоры в вектор-столбец R.
R = [L;P;C]
R=3×1 object
[3 1] array of linearRegressor, polynomialRegressor, customRegressor objects.
------------------------------------
1. Linear regressors in variables y1, u1
Variables: {'y1' 'u1'}
Lags: {[1] [2 5]}
UseAbsolute: [0 0]
TimeVariable: 't'
------------------------------------
2. Order 2 regressors in variables y1
Order: 2
Variables: {'y1'}
Lags: {[1]}
UseAbsolute: 0
AllowVariableMix: 0
AllowLagMix: 0
TimeVariable: 't'
------------------------------------
3. Custom regressor: y1(t-2).*u1(t-3)
VariablesToRegressorFcn: @(x,y)x.*y
Variables: {'y1' 'u1'}
Lags: {[2] [3]}
Vectorized: 1
TimeVariable: 't'
Regressors described by this set
Оцените нелинейную модель ARX с R.
sys = nlarx(z1,R)
sys = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: 1. Linear regressors in variables y1, u1 2. Order 2 regressors in variables y1 3. Custom regressor: y1(t-2).*u1(t-3) List of all regressors Output function: Wavelet Network with 1 unit Sample time: 0.1 seconds Status: Estimated using NLARX on time domain data "z1". Fit to estimation data: 59.73% (prediction focus) FPE: 3.356, MSE: 3.147
Просмотрите полный набор регрессоров.
getreg(sys)
ans = 5×1 cell
{'y1(t-1)' }
{'u1(t-2)' }
{'u1(t-5)' }
{'y1(t-1)^2' }
{'y1(t-2).*u1(t-3)'}
Загрузите данные оценки.
load iddata1;Создайте объект отображения сигмоидной сети с 10 модулями и без линейного термина.
SN = sigmoidnet(10,false);
Оцените нелинейную модель ARX. Подтвердите, что модель не использует линейную функцию.
sys = nlarx(z1,[2 2 1],SN); sys.OutputFcn.LinearFcn.Use
ans = logical
0
Загрузите данные оценки.
load throttledata;Детрендируйте данные.
Tr = getTrend(ThrottleData); Tr.OutputOffset = 15; DetrendedData = detrend(ThrottleData,Tr);
Оцените линейную модель ARX.
LinearModel = arx(DetrendedData,[2 1 1]);
Оцените нелинейную модель ARX с помощью линейной модели. Модели порядков, задержек и линейных параметров NonlinearModel получают из LinearModel.
NonlinearModel = nlarx(ThrottleData,LinearModel)
NonlinearModel = Nonlinear ARX model with 1 output and 1 input Inputs: Step Command Outputs: Throttle Valve Position Regressors: Linear regressors in variables Throttle Valve Position, Step Command List of all regressors Output function: Wavelet Network with 7 units Sample time: 0.01 seconds Status: Estimated using NLARX on time domain data "ThrottleData". Fit to estimation data: 99.03% (prediction focus) FPE: 0.1127, MSE: 0.1039
idnlarx ОбъектЗагрузите данные оценки.
load iddata1;Создайте idnlarx модель.
sys = idnlarx([2 2 1]);
Сконфигурируйте модель с помощью записи через точку:
Используйте объект отображения сигмоидной сети.
Присвойте имя.
sys.Nonlinearity = 'sigmoidnet'; sys.Name = 'Model 1';
Оцените нелинейную модель ARX со структурой и свойствами, заданными в idnlarx объект.
sys = nlarx(z1,sys)
sys = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: Linear regressors in variables y1, u1 List of all regressors Output function: Sigmoid Network with 10 units Name: Model 1 Sample time: 0.1 seconds Status: Estimated using NLARX on time domain data "z1". Fit to estimation data: 69.03% (prediction focus) FPE: 2.918, MSE: 1.86
Если оценка останавливается на локальном минимуме, можно возмущать модель, используя init и переоценить модель.
Загрузите данные оценки.
load iddata1;Оцените начальную нелинейную модель.
sys1 = nlarx(z1,[4 2 1],'sigmoidnet');Случайным образом возмущайте параметры модели, чтобы избежать локальных минимумов.
sys2 = init(sys1);
Оцените новую нелинейную модель с возмущенными значениями.
sys2 = nlarx(z1,sys1);
Загрузите данные оценки.
load twotankdata;Создайте iddata объект из данных оценки.
z = iddata(y,u,0.2);
Создайте nlarxOptions набор опций, задающий цель минимизации ошибок симуляции и максимум 50 итераций оценки.
opt = nlarxOptions;
opt.Focus = 'simulation';
opt.SearchOptions.MaxIterations = 50;Оцените нелинейную модель ARX.
sys = nlarx(z,[4 4 1],'sigmoidnet',opt)sys = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: Linear regressors in variables y1, u1 List of all regressors Output function: Sigmoid Network with 10 units Sample time: 0.2 seconds Status: Estimated using NLARX on time domain data "z". Fit to estimation data: 88.79% (simulation focus) FPE: 3.341e-05, MSE: 0.0004307
Загрузите данные примера регуляризации.
load regularizationExampleData.mat nldata;
Создайте sigmoidnet объект отображения с 30 модулями измерения и задавать порядки модели.
MO = sigmoidnet(30); Orders = [1 2 1];
Создайте набор опций оценки и установите метод поиска оценки на lm.
opt = nlarxOptions('SearchMethod','lm');
Оцените нерегулярную модель.
sys = nlarx(nldata,Orders,MO,opt);
Сконфигурируйте Lambda регуляризации параметр.
opt.Regularization.Lambda = 1e-8;
Оцените регуляризованную модель.
sysR = nlarx(nldata,Orders,MO,opt);
Сравните две модели.
compare(nldata,sys,sysR)

Большой отрицательный результат подгонки для нерегулизованной модели указывает на плохую подгонку к данным. Оценка регуляризованной модели дает значительно лучший результат.
data - Данные оценки во временной областиiddata объект | числовая матрицаДанные оценки временной области, заданные как iddata объект или числовая матрица.
Если data является iddata объект, затем data может иметь один или несколько выходных каналов и нуль или более входных каналов.
Если data является числовой матрицей, тогда количество столбцов данных должно совпадать с суммой количества входов (nu) и количеством выходов (ny.
data должны быть равномерно отобраны и не могут содержать отсутствующие (NaN) выборки.
orders - Заказы модели ARXnlarx порядки [na nb nk]Порядки модели ARX, заданные как матрица [na nb nk]. na обозначает количество отложенных выходов, nb обозначает количество запаздывающих входов и nk обозначает минимальную входную задержку. Минимальная выходная задержка фиксирована на 1. Для получения дополнительной информации о том, как создать orders матрица, см. arx.
Когда вы задаете orders, программное обеспечение преобразует информацию о порядке в линейную форму регрессора в idnlarx
Regressors свойство. Для получения примера смотрите Создание нелинейной модели ARX с использованием Порядков ARX Model.
regressors - спецификации к регрессоруlinearRegressor | объекта polynomialRegressor | объекта customRegressor объект | массив столбцов объектов спецификаций регрессораСпецификация регрессора, заданная как вектор-столбец, содержащая один или несколько объектов спецификации регрессора, которые являются linearRegressor объекты, polynomialRegressor объекты, и customRegressor объекты. Каждый объект задает формулу для генерации регрессоров из отстающих переменных. Для примера:
L = linearRegressor({'y1','u1'},{1,[2 5]}) генерирует регрессоры y1 (t -1), u1 (t -2) и u2 (t -5).
P = polynomialRegressor('y2',4:7,2) генерирует регрессоры y2 (t -4)2, y2 (t –5)2, y2 (t –6)2, и y2 (t-7)2.
C = customRegressor({'y1','u1','u2'},{1 2 2},@(x,y,z)sin(x.*y+z)) генерирует один регрессор sin (y1 (t -1) u1 (t -2) + u2 (t -2)).
Когда вы создаете набор регрессоров, чтобы поддержать оценку с помощью iddata можно использовать входные и выходные имена объекта, а не создавать имена для функции регрессора. Например, предположим, что вы создаете линейный регрессор для модели, планируйте использовать iddata z объекта для оценки модели. Для создания линейного регрессора можно использовать следующую команду.
L = linearRegressor([z.outputName;z.inputName],{1,[2 5]})Для примера создания и использования набора линейных регрессоров SISO, смотрите Оценку нелинейной модели ARX с использованием набора линейных регрессоров. Для примера создания линейного регрессорного набора MIMO, который получает имена переменных из набора данных оценки, см. Оценку нелинейной модели ARX MIMO с той же функцией отображения для всех выходов.
output_fcn - Выходная функция'wavenet' (по умолчанию) | 'linear' | [] | '' | 'sigmoidnet' | 'treepartition' | 'neuralnet' | 'customnet' | объект отображения | массив объектов отображенияВыходная функция, которая отображает регрессоры idnlarx модель в выходы модели, заданная как массив столбцов, содержащий нуль или более из следующих строк или объектов:
'wavenet' или wavenet объект | Вейвлет |
'linear' или '' или [] или linear объект | Линейная функция |
'sigmoidnet' или sigmoidnet объект | Сигмоидная сеть |
'treepartition' или treepartition объект | Бинарная модель регрессии древовидного разбиения |
neuralnet объект | Нейронная сеть - Сеть прямого распространения Toolbox™ Глубокого Обучения. |
customnet объект | Настраиваемая сеть - аналогично sigmoidnet, но с определяемой пользователем заменой сигмоидной функции. |
Используйте строку, например 'sigmoidnet', для использования свойств по умолчанию объекта функции отображения. Используйте сам объект, например sigmoidnet, когда необходимо сконфигурировать свойства объекта отображения.
wavenet, sigmoidnet, treepartion, и customnet объекты содержат как линейные, так и нелинейные компоненты. Можно удалить (не использовать) линейные компоненты wavenet, sigmoidnet, и customnet путем установки LinearFcn.Use значение в false.
neuralnet функция имеет только нелинейный компонент, который network (Deep Learning Toolbox) объекта Deep Learning Toolbox. Линейная функция, как подразумевается в имени, имеет только линейный компонент.
output_fcn является статическим, поскольку он зависит только от значений данных в определенное время, но не непосредственно от самого времени. Например, если выходная функция y (<reservedrangesplaceholder14>)
равна y0 + <reservedrangesplaceholder12> <reservedrangesplaceholder11>
(t-1) + <reservedrangesplaceholder9> <reservedrangesplaceholder8>
(t-2) +... b1 u (t -1) + b2 u (t -2) +..., затем output_fcn является линейной функцией, которую linear Отображение объекта представляет.
Установка вектора символов, для примера 'sigmoidnet'создает объект отображения с настройками по умолчанию. Кроме того, можно задать отображение свойств объекта двумя способами:
Создайте объект отображения с помощью аргументов для изменения свойств по умолчанию.
MO = sigmoidnet(15);
Сначала создайте объект отображения по умолчанию, а затем используйте запись через точку для изменения свойств.
MO = sigmoidnet; MO.NumberOfUnits = 15;
Для ny выходных каналов можно задать объекты отображения индивидуально для каждого канала путем установки output_fcn в массив ny отображения объектов. Для примера следующий код задает OutputFcn использование записи через точку для системы с двумя входными каналами и двумя выходными каналами.
sys = idnlarx({'y1','y2'},{'u1','u2'});
sys.OutputFcn = [wavenet; sigmoidnet];OutputFcn как вектор символов или один объект отображения.
output_fcn представляет статическую функцию отображения, которая преобразует регрессоры нелинейной модели ARX в выходы модели. output_fcn является статическим, потому что это не зависит от времени. Для примера, если , затем output_fcn является линейной функцией, представленной linear объект.
Пример определения выходной функции см. в разделе Определение и настройка выходной функции.
linmodel - Линейная модель в дискретном времениidpoly | объекта idss | объекта idtf | объекта idproc объектsys0 - Нелинейная модель ARXidnlarx модельНелинейная модель ARX, заданная как idnlarx модель. sys0 могут быть:
Модель, ранее оцененная с использованием nlarx. Алгоритм оценки использует параметры sys0 как исходные догадки. В этом случае используйте init чтобы слегка возмущать свойства модели, чтобы избежать захвата модели в локальных минимумах.
sys = init(sys); sys = nlarx(data,sys);
Модель, ранее созданная с использованием idnlarx конструктор и со свойствами, установленными с помощью записи через точку. Например, используйте следующее, чтобы создать объект idnlarx, задать его свойства и оценить модель.
sys1 = idnlarx('y1','u1',Regressors); sys1.OutputFcn = 'treepartition'; sys1.Ts = 0.02; sys1.TimeUnit = 'Minutes'; sys1.InputName = 'My Data'; sys2 = nlarx(data,sys1);
Предыдущий код эквивалентен следующей команде nlarx.
sys2 = nlarx(data,Regressors,'treepartition','Ts',0.02,'TimeUnit','Minutes', ... 'InputName','My Data');
Options - опции оценкиnlarxOptions набор опцийОпции оценки для нелинейной идентификации модели ARX, заданные как nlarxOptions набор опций.
sys - Нелинейная модель ARXidnlarx объектНелинейная модель ARX, которая соответствует данным оценки, возвращенная как idnlarx объект. Эта модель создается с использованием заданных порядков моделей, нелинейности и опций оценки.
Информация о результатах оценки и используемых опциях хранится в Report свойство модели. Содержимое Report зависят от выбора нелинейности и оценочного фокуса, который вы указали для nlarx. Report имеет следующие поля:
| Поле отчета | Описание | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Status | Сводными данными статуса модели, которое указывает, была ли модель создана конструкцией или получена оценкой. | ||||||||||||||||||
Method | Используется команда estimation. | ||||||||||||||||||
Fit | Количественная оценка оценки, возвращенная как структура. Смотрите функции потерь и метрики качества модели для получения дополнительной информации об этих метриках качества. Структура имеет следующие поля:
| ||||||||||||||||||
Parameters | Оценочные значения параметров модели. | ||||||||||||||||||
OptionsUsed | Набор опций, используемый для оценки. Если пользовательские опции не были настроены, это набор опций по умолчанию. Посмотрите | ||||||||||||||||||
RandState | Состояние потока случайных чисел в начале оценки. Пустой, | ||||||||||||||||||
DataUsed | Атрибуты данных, используемых для оценки, возвращаются как структура со следующими полями:
| ||||||||||||||||||
Termination | Условия завершения итерационного поиска, используемого для минимизации ошибки предсказания, возвращаются как структура со следующими полями:
Для методов оценки, которые не требуют численной оптимизации поиска, |
Для получения дополнительной информации об использовании Report, см. Отчет по оценке.
Нелинейная модель ARX состоит из регрессоров модели и выходной функции. Выходная функция включает линейные и нелинейные функции, которые действуют на регрессоры модели, чтобы дать выход модели и фиксированное смещение для этого выхода. Этот блок представляет структуру нелинейной модели ARX в сценарии симуляции.
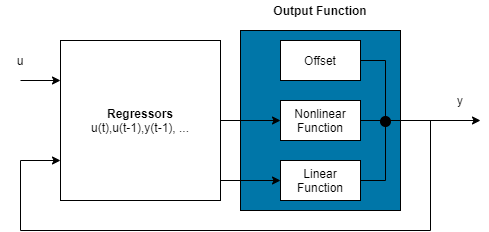
Программа вычисляет выходные y нелинейной модели ARX в два этапа:
Он вычисляет значения регрессора из текущих и прошлых входных значений и прошлых выходных данных.
В самом простом случае регрессоры являются задержанными входами и выходами, такими как u (t -1) и y (t -3). Такие регрессоры называются linear regressors. Линейные регрессоры задаются с помощью linearRegressor объект. Можно также задать линейные регрессоры при помощи заказов линейной модели ARX в качестве входного параметра. Для получения дополнительной информации см. «Нелинейные порядки модели ARX» и «Задержка». Однако этот второй подход ограничивает набор регрессоров линейными регрессорами с последовательными задержками. Чтобы создать polynomial regressors, используйте polynomialRegressor объект. Можно также задать custom regressors, которые являются нелинейными функциями задержанных входов и выходов. Например, u (t -1) y (t -3) является пользовательским регрессором, который умножает образцы входа и выхода вместе. Задайте пользовательские регрессоры, используя customRegressor объект.
Можно назначить любой из регрессоров в качестве входов линейному функциональному блоку выходной функции, нелинейному функциональному блоку или обоим.
Он преобразует регрессоры в выходные данные модели с помощью блока выходной функции. Блок выходной функции может включать линейные и нелинейные блоки параллельно. Для примера рассмотрим следующее уравнение:
Здесь x является вектором регрессоров, а r - средним значением x. - выход блока линейной функции. представляет выход нелинейного функционального блока. Q является проекционной матрицей, которая делает вычисления хорошо обусловленными. d является скалярным смещением, которое добавляется к комбинированным выходам линейного и нелинейного блоков. Точная форма F (x) зависит от вашего выбора выходной функции. Можно выбрать из доступных объектов отображения, таких как сети древовидного раздела, вейвлет и многослойные нейронные сети. Можно также исключить из выходной функции линейный или нелинейный функциональный блок.
При оценке нелинейной модели ARX программное обеспечение вычисляет значения параметров модели, такие как L, r, d, Q и другие параметры, задающие g.
Получившиеся нелинейные модели ARX idnlarx объекты, которые хранят все данные модели, включая регрессоры модели и параметры выходной функции. Для получения дополнительной информации об этих объектах см. Раздел «Нелинейные структуры модели».
idnlarx свойства не рекомендованы.Не рекомендуемый запуск в R2021a
Начиная с R2021a, несколько свойств idnlarx были изменены или заменены.
Эти изменения влияют на синтаксис в обоих idnlarx и nlarx. Использование свойств pre-R2021a в следующей таблице не рекомендуется. Однако программное обеспечение все еще принимает синтаксисы вызова, которые включают эти свойства. В настоящее время нет планов исключать эти синтаксисы. Синтаксис команды, который использует порядки модели ARX, продолжается, является рекомендуемым синтаксисом.
| Pre-R2021a свойства | R2021a свойства | Использование |
|---|---|---|
Модель ARX порядков na,nb,nk | Regressors, который может включать в себя linearRegressor, polynomialRegressor, и customRegressor объекты. |
Вы больше не можете изменять значения порядков в существующей |
customRegressors | Regressors | Использование polynomialRegressor или customRegressor чтобы создать объекты регрессора и добавить объекты в Regressors массив. |
NonlinearRegressors | RegressorUsage | RegressorUsage - таблица, содержащая назначения регрессора линейным и нелинейным выходным компонентам. Измените назначения путем изменения соответствующих RegressorUsageзаписи таблицы. |
Nonlinearity | OutputFcn | Изменение имеет только имя. Свойство остается объектом или массивом или объектами, которые сопоставляют входы регрессора с выходом. |
Поддержка параллельных вычислений доступна для оценки с помощью lsqnonlin метод поиска (требует Optimization Toolbox™). Чтобы включить параллельные вычисления, используйте nlarxOptions, задать SearchMethod на 'lsqnonlin', и задать SearchOptions.Advanced.UseParallel на true, как в следующем примере.
opt = nlarxOptions;
opt.SearchMethod = 'lsqnonlin';
opt.SearchOptions.Advanced.UseParallel = true;
aic | fpe | goodnessOfFit | idnlarx | isnlarx | linearRegressor | nlarxOptions | polynomialRegressor
У вас есть измененная версия этого примера. Вы хотите открыть этот пример с вашими правками?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.