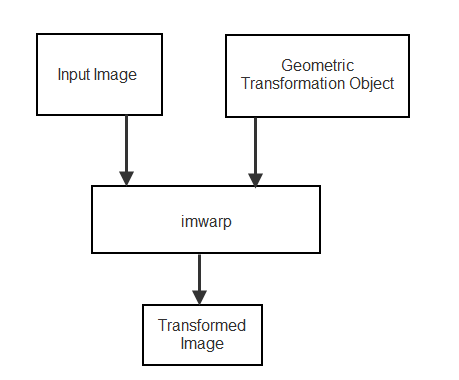
Чтобы выполнить 2-D или 3-D геометрическое преобразование, сначала создайте объект геометрического преобразования, который хранит информацию о преобразовании. Затем передайте изображение, которое будет преобразовано, и объект геометрического преобразования в imwarp функция. Вы опционально можете предоставить пространственную ссылочную информацию о входе изображении, чтобы imwarp.
Различные типы объектов геометрического преобразования хранят разную информацию о преобразовании.
The rigid2d, affine2d, projective2d, rigid3d, и affine3d объекты хранят матрицу преобразования.
The geometricTransform2d и geometricTransform3d объекты сохраняют обратную точечную функцию отображения и, опционально, прямую точечную функцию отображения.
Другие типы преобразования, включая LocalWeightedMeanTransformation2D, PiecewiseLinearTransformation2D, и PolynomialTransformation2D объекты, сохраните отображение между парами контрольных точек.
Существует несколько способов создать геометрический объект преобразования.
| Подход к созданию объекта преобразования | affine2d | affine3d |
| projective2d |
| Другие объекты преобразования |
|---|---|---|---|---|---|---|
| Задайте матрицу преобразования | X | X | X | X | ||
| Задайте пользовательскую функцию отображения точек | X | |||||
| Вычислите преобразование из пар точек управления | X | X | X | |||
| Оцените преобразование, используя оптимизацию подобия | X | X | ||||
| Оцените преобразование, используя Фазу корреляцию | X |
Если вы знаете матрицу преобразования для геометрического преобразования, которое вы хотите выполнить, то можно создать rigid2d, affine2d, projective2d, rigid3d, или affine3d геометрический объект преобразования непосредственно. Для получения дополнительной информации о создании матрицы преобразования см. «Матричное представление геометрических преобразований».
Следующий пример задает матрицу преобразования для 2-D перевода и создает affine2d геометрический объект преобразования.
xform = [ 1 0 0
0 1 0
40 40 1 ];
tform_translate = affine2d(xform)tform_translate =
affine2d with properties:
T: [3x3 double]
Dimensionality: 2Если у вас есть обратная функция точечного отображения, то можно задать пользовательское 2-D и 3-D геометрическое преобразование с помощью geometricTransform2d и geometricTransform3d объекты соответственно.
Следующий пример задает функцию обратного отображения, которая принимает и возвращает 2-D точки в упакованном (x, y) формате. Затем в примере создается geometricTransform2d пользовательский объект геометрического преобразования.
inversefn = @(c) [c(:,1)+c(:,2),c(:,1).^2]
inversefn =
function_handle with value:
@(c)[c(:,1)+c(:,2),c(:,1).^2]tform = geometricTransform2d(inversefn)
tform =
geometricTransform2d with properties:
InverseFcn: [function_handle]
ForwardFcn: []
Dimensionality: 2Точно так же в следующем примере создается geometricTransform3d пользовательский объект геометрического преобразования с помощью функции обратного отображения. Пример задает функцию обратного отображения, которая принимает и возвращает 3-D точки в упакованном (x, y, z) формате.
inversefn = @(c)[c(:,1)+c(:,2),c(:,1)-c(:,2),c(:,3).^2]
inversefn =
function_handle with value:
@(c)[c(:,1)+c(:,2),c(:,1)-c(:,2),c(:,3).^2]tform = geometricTransform3d(inversefn)
tform =
geometricTransform3d with properties:
InverseFcn: [function_handle]
ForwardFcn: []
Dimensionality: 3Можно создать объект геометрического преобразования путем передачи двух наборов пар точек управления в fitgeotrans функция. The fitgeotrans функция автоматически оценивает преобразование из этих точек и возвращает один из геометрических объектов преобразования.
Различные преобразования требуют различного числа точек. Для примера аффинные преобразования требуют трех неколлинеарных точек в каждом изображении (треугольник) и проективные преобразования требуют четырех точек (четырёхугольник).
Этот пример передает два набора управляющих точек в fitgeotrans, который возвращает affine2d геометрический объект преобразования.
movingPoints = [11 11;21 11; 21 21];
fixedPoints = [51 51;61 51;61 61];
tform_cpp = fitgeotrans(movingPoints,fixedPoints,'affine')
tform_cpp =
affine2d with properties:
T: [3x3 double]
Dimensionality: 2Если у вас есть фиксированное изображение и движущееся изображение, которые немного смещены, то вы можете использовать imregtform функция для оценки аффинного геометрического преобразования, которое выравнивает изображения. imregtform оптимизирует среднее значение квадратов или метрику взаимного информационного подобия Маттеса двух изображений, используя регулярный ступенчатый градиентный спуск или эволюционный оптимизатор «один плюс один». Для получения дополнительной информации смотрите Создание Оптимизатора и Метрика для регистрации изображений на основе интенсивности.
Если у вас есть фиксированное изображение и движущееся изображение, которые сильно рассогласованы, то вы можете использовать imregcorr функция для оценки аффинного геометрического преобразования, которое улучшает выравнивание изображения. Можно уточнить полученное преобразование с помощью оптимизации подобия.
После того, как вы определите преобразование в объекте геометрического преобразования, выполните преобразование с помощью imwarp функция. При вызове функции задайте изображение, которое будет преобразовано, и объект геометрического преобразования.
imwarp использует геометрическое преобразование, чтобы сопоставить координаты в выходном изображении с соответствующими координатами в вход изображении (обратное отображение). Затем, imwarp использует отображение координат, чтобы интерполировать значения пикселей в вход изображении и вычислить значение выхода пикселя.
affine2d | affine3d | fitgeotrans | geometricTransform2d | geometricTransform3d | imwarp | projective2d | rigid2d | rigid3d