Сферические координаты

Поддержка сферических координат

Сферические координаты описывают вектор или точку в пространстве с расстоянием и двумя углами. Расстояние, R, является обычной нормой Евклида. Существует несколько соглашений относительно спецификации двух углов. Они включают в себя:

Азимут и углы возвышения
Углы Phi и theta
u и v координаты

Программное обеспечение Phased Array System Toolbox™ изначально поддерживает представление азимута/высоты. Программное обеспечение также предоставляет функции для преобразования между представлением азимута/высоты и другими представлениями. См. Phi и Theta Углов и U и V координаты.

Азимут и углы возвышения

В программном обеспечении Phased Array System Toolbox преобладающим условием для сферических координат является следующее:

Используйте угол азимута, az и угла возвышения, el, чтобы определить местоположение точки на сферу единичного радиуса.
Задайте все углы в степенях.
Список координаты в последовательности (az, el, R).

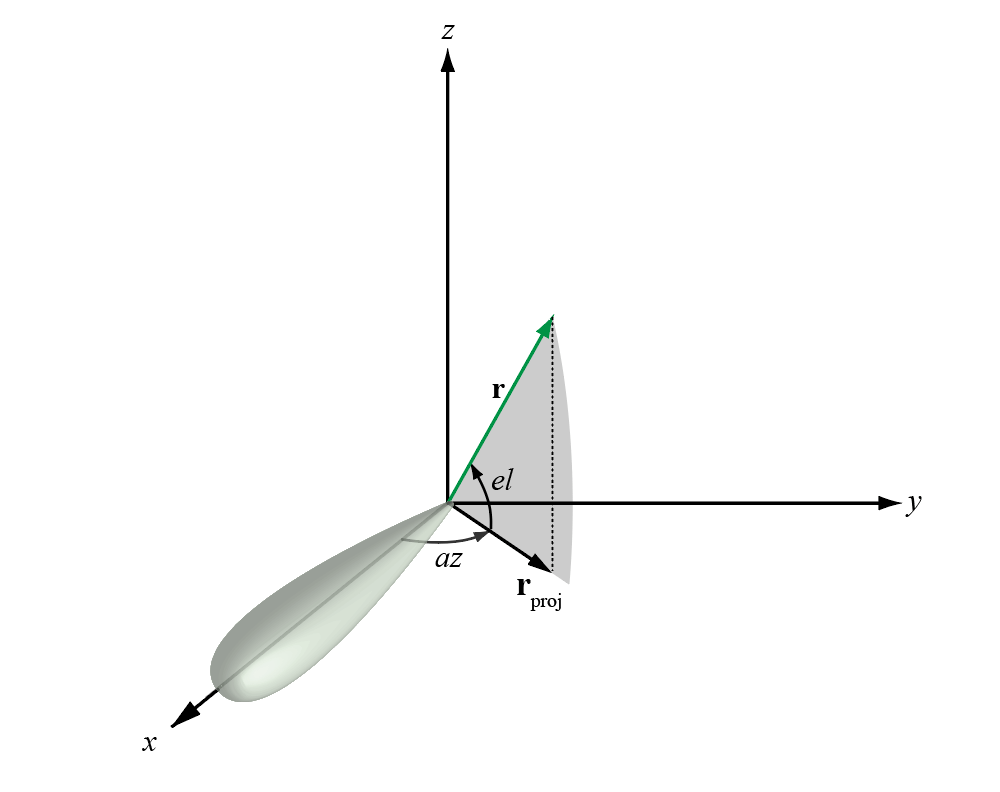
azimuth angle вектора является угол между осью x и ортогональной проекцией вектора на плоскость xy. Угол положителен в движении от оси x к оси y. Азимутальные углы лежат между -180 и 180 степенями. elevation angle является углом между вектором и его ортогональной проекцией на xy -плоск. Угол положителен при движении к положительной оси z от плоскости xy. По умолчанию направление boresight элемента или массива выровнено с положительной осью x -. Направление boresight является направлением основной лепестка элемента или массива.

Примечание

Угол возвышения иногда определяется в литературе как угол, который вектор делает с положительной осью z -. MATLAB^® и продукты Phased Array System Toolbox не используют это определение.

Этот рисунок иллюстрирует угол азимута и угол возвышения для вектора, показанного в виде зеленой сплошной линии.

Углы Фи и Теты

В качестве альтернативы азимуту и углам возвышения можно использовать углы, обозначенные φ и θ, чтобы выразить расположение точки на сферу единичного радиуса. Чтобы преобразовать представление φ/θ в и из соответствующего представления азимута/высоты, используйте функции преобразования координат, phitheta2azel и azel2phitheta.

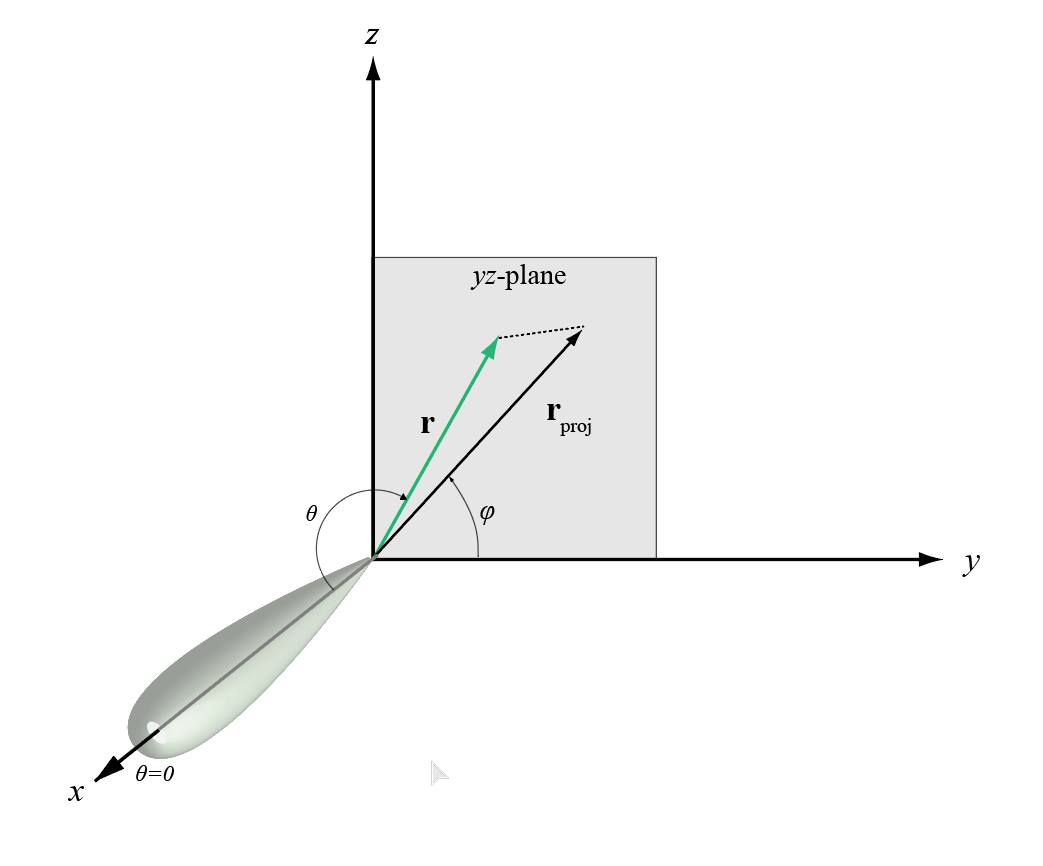
Угол phi (φ) является углом от положительной оси y до ортогональной проекции вектора на плоскость yz. Угол положителен к положительной оси z -. Угол phi находится между 0 и 360 степенями. Угол theta (θ) является углом от оси x до самого вектора. Угол положительный к плоскости yz. Угол theta находится между 0 и 180 степенями.

Рисунок иллюстрирует phi и theta для вектора, который появляется в виде зеленой сплошной линии.

Координатные преобразования между и az/el описываются следующими уравнениями

$\begin{array}{l} \sin e l = \sin ϕ \sin θ \\ \tan a z = \cos ϕ \tan θ \\ \cos θ = \cos e l \cos a z \\ \tan ϕ = \tan e l / \sin a z \end{array}$

Координаты U и V

В радиолокационных приложениях часто полезно параметризовать полусферу x ≥ 0 с помощью координат, обозначенных u и v.

Чтобы преобразовать представление в и из соответствующего представления u/ v, используйте функции координатного преобразованияphitheta2uv и uv2phitheta.
Чтобы преобразовать представление азимута/высоты в и из соответствующего представления u/ v, используйте функции координатного преобразованияazel2uv и uv2azel.

Можно задать u и v в терминах

$\begin{array}{l} u = \sin θ \cos ϕ \\ v = \sin θ \sin ϕ \end{array}$

В этих выражениях φ и θ - phi и углы theta, соответственно.

По азимуту и повышению u и v координаты

$\begin{array}{l} u = \cos e l \sin a z \\ v = \sin e l \end{array}$

Значения u и v удовлетворяют неравенствам

$\begin{array}{l} - 1 \leq u \leq 1 \\ - 1 \leq v \leq 1 \\ u^{2} + v^{2} \leq 1 \end{array}$

И наоборот, углы phi и theta могут быть написаны с точки зрения u и v с помощью

$\begin{array}{l} \tan ϕ = v / u \\ \sin θ = \sqrt{u^{2} + v^{2}} \end{array}$

Азимут и углы возвышения также могут быть записаны в терминах u и v:

$\begin{array}{l} \sin e l = v \\ \tan a z = \frac{u}{\sqrt{1 - u^{2} - v^{2}}} \end{array}$

Преобразование между прямоугольной и сферической координатами

Следующие уравнения определяют отношения между прямоугольными координатами и (az, el, R) представлением, используемым в программном обеспечении Phased Array System Toolbox.

Для преобразования прямоугольных координат в (az, el, R):

$\begin{array}{l} R = \sqrt{x^{2} + y^{2} + z^{2}} \\ a z = \tan^{- 1} (y / x) \\ e l = \tan^{- 1} (z / \sqrt{x^{2} + y^{2}}) \end{array}$

Для преобразования (az, el, R) в прямоугольные координаты:

$\begin{array}{l} x = R \cos (e l) \cos (a z) \\ y = R \cos (e l) \sin (a z) \\ z = R \sin (e l) \end{array}$

При указании местоположения целевого устройства относительно фазированной решетки обычно ссылается на его расстояние и направление от массива. Расстояние от массива соответствует R в сферических координатах. Направление соответствует азимуту и углам возвышения.

Совет

Для преобразования между прямоугольными координатами и (az, el, R) используйте функции MATLABcart2sph и sph2cart. Эти функции задают углы в радианах. Для преобразования между степенями и радианами используйте deg2rad и rad2deg.

Широкоугольные углы

Broadside angles полезны при описании отклика равномерного линейного массива (ULA). Реакция массива зависит непосредственно от широкого угла, а не от азимута и углов возвышения. Начните с ULA и нарисуйте плоскость, ортогональную оси ULA, как показано синим цветом на рисунке. Широкий угол, β, является углом между плоскостью и направлением сигнала. Чтобы вычислить широкий угол, создайте линию от любой точки на пути сигнала до плоскости, ортогональной плоскости. Угол между этими двумя линиями является широким углом и лежит в интервале [-90 °, 90 °]. Широкий угол положителен при измерении в положительном направлении оси массива. Ноль степеней указывает путь сигнала, ортогональный оси массива. ± 90 ° указывает пути вдоль оси массива. Все сигнальные пути, имеющие одинаковый широкий угол, образуют конус вокруг оси ULA.

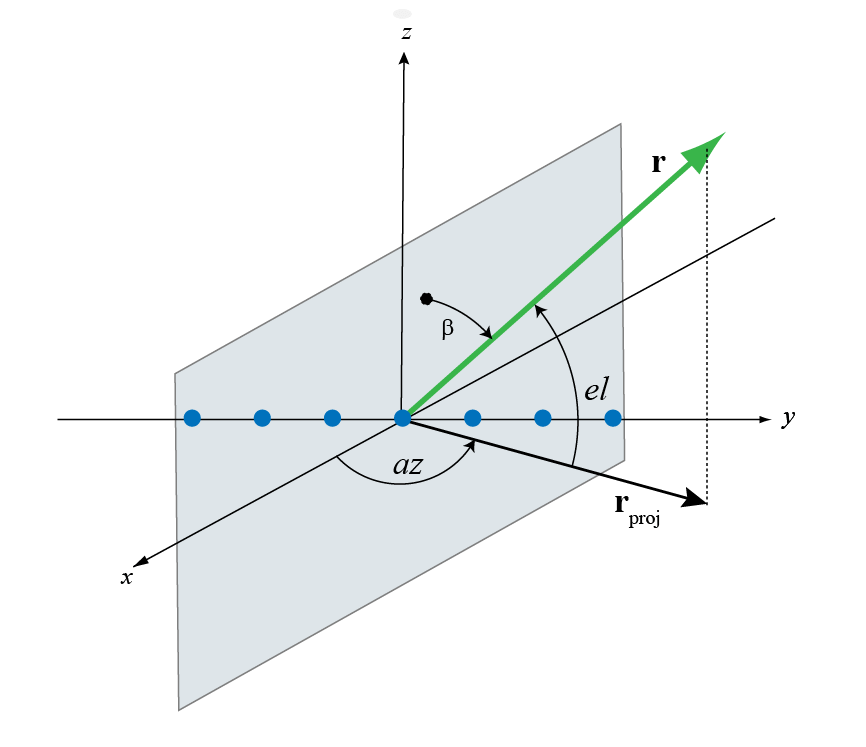
Преобразование из угла азимута, az и угла возвышения, el, в широкий угол, β, является

$β = \sin^{- 1} (\sin (a z) \cos (e l))$

Это уравнение показывает, что

Для угла возвышения нуля широкий угол равен азимутальному углу.
Углы возвышения одинаково выше и ниже плоскости xy приводят к одинаковым широким углам.

Можно преобразовать из широкого угла в угол азимута, но необходимо задать угол возвышения

$a z = \sin^{- 1} (\frac{\sin β}{\cos (e l)})$

Поскольку пути сигналов для заданного широкого угла, β, образуют конус вокруг оси массива, вы не можете задавать угол возвышения произвольно. Угол возвышения и широкий угол должны удовлетворять

$| e l | + | β | \leq 90$

Следующий рисунок изображает ULA с элементами, разнесенными на d метров вдоль оси y. ULA облучается плоской волной, излучаемой источником точки в дальнем поле. Для удобства угла возвышения равен нулю степеней. В этом случае направление сигнала лежит в xy -плане. Затем широкий угол уменьшается до азимутального угла.

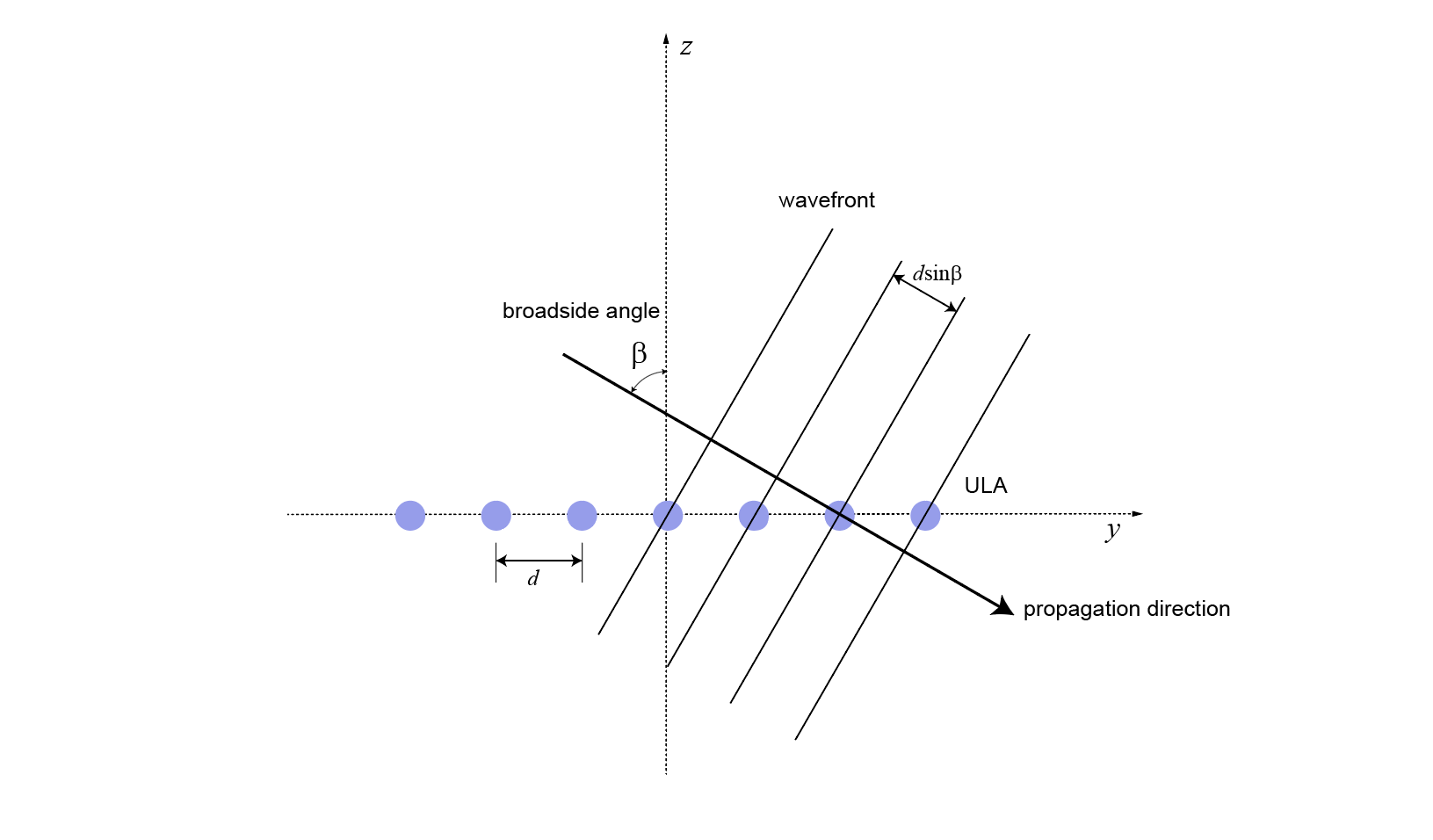
Из-за угла прибытия элементы массива не освещаются одновременно плоской волной. Дополнительное расстояние, на которое падающая волна перемещается между элементами массива d sinβ где d расстояние между элементами массива. Постоянная задержка, τ, между элементами массива

$τ = \frac{d \sin β}{c},$

где c - скорость волны.

Для широких углов ± 90 ° сигнал падает на массив, параллельную оси массива, и задержка времени между датчиками равна ±d/c. Для широкого нулевого угла плоская волна освещает все элементы ULA одновременно, и временная задержка между элементами равна нулю.

Программное обеспечение Phased Array System Toolbox обеспечивает функции az2broadside и broadside2az для преобразования между азимутом и широкими углами.

Преобразование между широкоугольными углами и азимутом и повышением

Открыть Live Script

Следующие примеры показывают, как использовать az2broadside и broadside2az функций.

Цель расположена под азимутальным углом 45 ° и под угол возвышения 60 ° относительно ULA. Определите соответствующий широкий угол.

bsang = az2broadside(45,60)

bsang = 20.7048

Вычислите азимут для падающего сигнала, поступающего под широким углом 45 ° и вертикальным 20 °.

az = broadside2az(45,20)

az = 48.8063

Документация