Flexible Shaft

Вал с кручением и изгибом податливости

Библиотека:
Simscape/Driveline/Муфты и приводы

Описание

Блок Flexible Shaft представляет приводной вал с кручением и изгибом податливости. Вал состоит из гибкого материала, который скручивается в ответ на приложенный крутящий момент и изгибается в ответ на статический дисбаланс массы. Скручивающее действие задерживает передачу степени между концами вала, изменяя динамическую характеристику системы привода.

Чтобы представлять гибкий для кручения вал, блок использует метод кусковой массы. Эта модель разделяет вал на различные элементы, которые соединяются между собой через параллельные системы демпфера пружины. Элементы обеспечивают инерцию вала, в то время как системы демпфера пружины обеспечивают податливость вала.

Блок предоставляет четыре метода параметризации, которые позволяют вам моделировать податливость либо в однородном, либо в аксиально неоднородном валу. Аксиально неоднородный вал является таким, для которого любой из этих атрибутов изменяется по длине вала:

Кручение жесткости
Инерция кручения
Жесткость при изгибе
Плотность
Модуль сдвига
Модуль Янга
Внешний диаметр
Внутренний диаметр

Дополнительный параметр позволяет вам смоделировать потери степени в подшипниках из-за вязкого трения на концах вала. Для получения дополнительной информации см. Torsion Модели.

Примечание

Вязкое трение на концах вала отличается от внутреннего демпфирования материала, что соответствует потерям, возникающим в самом материале вала.

Чтобы представлять гибкий вал с изгибом, блок использует или метод кусковой массы, или метод собственных моделей. В то время как метод кусковой массы проще сконфигурировать, метод собственных моделей имеет тенденцию моделировать быстрее.

Совет

Если скорость симуляции, является высоким приоритетом, сначала моделируйте с помощью метода сглаженной массы, корректируя параметры по мере необходимости, пока результаты не совпадут с вашими математическими моделями или экспериментальными данными. Далее моделируйте с помощью метода eigenmodes. Снова корректируйте параметры по мере необходимости до результатов математических моделей или экспериментальных данных. Для примера, который использует оба метода, см. Вал с кручением и поперечной гибкостью.

Для метода кусковой массы количество элементов гибочного вала совпадает с количеством элементов кручения вала. Модель делит вал на ряд таких элементов. Элементы обеспечивают инерцию вала, в то время как матрицы жесткости обеспечивают податливость вала. Метод eigenmodes вычисляет эффективные системы масса-пружина-демпфер, которые представляют режимы изгиба вала. Можно задать количество включаемых режимов и точность форм режимов. И методы кусковой массы, и методы собственных моделей позволяют вам моделировать:

Возбуждающие статические дисбалансы
Концентрически присоединенные твердые массы
До четырёх поддержек расположений вдоль вала
Линейное демпфирование, пропорциональное инерции вала
Линейное демпфирование, пропорциональное жесткости вала

Примечание

Метод собственных моделей принимает, что поддержка является легким по сравнению с жесткостью поддержки.

Статические дисбалансы, которые возбуждают изгиб, возникают, когда центр масс вала или прикрепленная жесткая масса не выровнена с основной осью вала. Можно варьировать местоположения, величины и смещения угла статических дисбалансов на валу.

Можно представлять концентрически прикрепленные твердые массы как диски или идеализированные точки массы. Концентрический диск добавляет диаметральные и полярные моменты инерции к валу и массе к степени свободы перемещения узлов вала. Модель принимает, что диск тонкий, поэтому вал все еще может сгибаться с любой стороны осевого положения вместе с диском. Полярный момент инерции связывает две плоскости изгиба. Концентрическая точка масса является идеализированной версией концентрического диска. Концентрическая масса точки добавляет массу к степеням свободы перемещения узлов вала, но не имеет вращательных моментов инерции. Можно варьировать местоположения и инерцию концентрических дисков или точечных масс, присоединенных к валу.

Можно смоделировать поддержки как идеальные или с помощью матриц жесткости и демпфирования. Для каждой поддержки можно варьировать:

Расположение - Любая точка вдоль длины вала.
Тип - Идеальный зажим, идеальный контакт, свободный, постоянная жесткость и демпфирование подшипника, или зависимая от скорости жесткость и демпфирование.
Число - Два, три, или четыре.

Для обоих методов изгиба можно задать податливость изгиба вала с помощью жесткости изгиба и линейной плотности массы или модуля Юнга и диаметра вала.

Можно параметризовать модель кручения с помощью k жесткости и инерции J или размерностей и свойств материала вала.

Модель кручения

Для модели кручения Flexible Shaft блок аппроксимирует распределенные, непрерывные свойства вала с помощью метода кусковой массы. Модель содержит конечное число, N, последовательно сглаженных инерцией пружинных элементов плюс конечная инерция. Результатом является серия из $N + 1$ инерция, соединенная N пружинами вращения и N демпферами вращения.

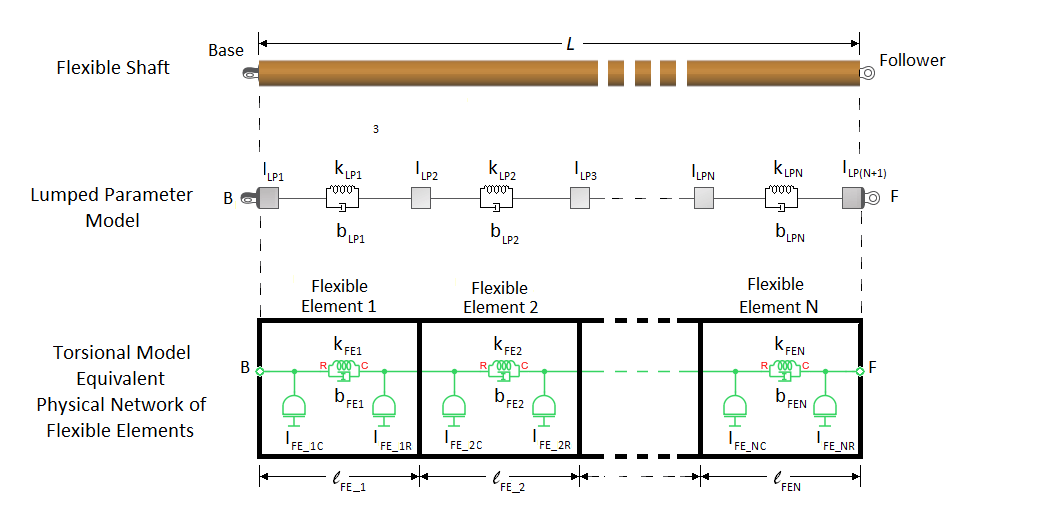
Блок моделирует вал как эквивалентную физическую сеть N гибких элементов. Каждый гибкий элемент _FEi представляет собой короткий участок приводного вала и содержит:

Одна пружина, _{kFE_i}, для кручения податливости. Сеть имеет в общей сложности N пружин.
Один демпфер, _{bFE_i}, для демпфирования материала. Сеть имеет в общей сложности N демпферов.
Две инерции, _{IFE_iC} и _{IFE_iR}, для сопротивления вращению. Инерция соседних гибких элементов консолидируется вместе, так что сеть имеет в общей сложности $N + 1$ инерция.

Для аксиально однородного вала длины гибкого элемента, податливость, демпфирование и распределенные инерции в физической сети равны, так что:

$l_{F E_1} = l_{F E_2} = \dots = l_{F E_N} = \frac{L}{N}$

$k_{F E_1} = k_{F E_2} = \dots = k_{F E_N} = k$

$b_{F E_1} = b_{F E_2} = \dots = b_{F E_N} = b$

$I_{F E_1C} = I_{F E_1R} = I_{F E_2C} = I_{F E_2R} = \dots = I_{F E_N C} = I_{F E_N R} = \frac{I}{2 N}$

Для аксиально неоднородного вала величина податливости, демпфирования и инерция R -узлов и C - узлов может различаться для отдельных гибких элементов в модели физической сети.

Алгоритм размещения узлов

Баланс между точностью модели и скоростью симуляции зависит от N, количества гибких элементов, которые использует блок, чтобы представлять вал. Для получения информации о балансировке скорости симуляции и точности модели, смотрите Улучшить скорость симуляции или Точность.

Блок позволяет вам задать минимальное количество гибких элементов, _Nmin, как значение для параметра Минимальное количество гибких элементов. Однако количество гибких элементов, которые на самом деле использует блок, зависит от сложности вала, который он моделирует. Если блок требует более гибких элементов, чем вы задаете, чтобы решить модель, которая содержит аксиальную неоднородность, промежуточные поддержки, концентрические диски или массы или статические дисбалансы, то $N \geq N_{\min}$ .

Например, предположим, что для сложного вала в схеме вы задаете осевые положения для поддержек, статический дисбаланс, сечение большего диаметра и концентрический диск. Вы устанавливаете параметр для _Nmin равным 7.

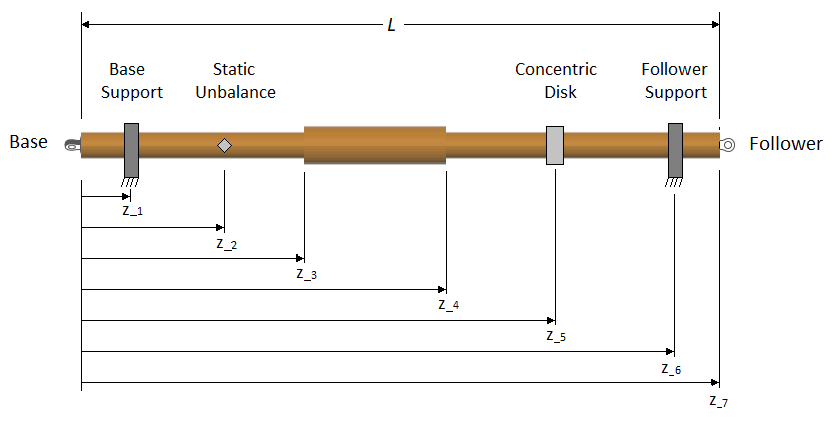
Если гибка модели включена, положения гибкого элемента модели кручения учитывают положения статических дисбалансов и концентрических жестких масс, так что гибкие элементы кручения совпадают с гибкими элементами гибки. Во время симуляции модель кручения не зависит от любых статических дисбалансов или концентрических жестких масс.

Алгоритм для блока определяет количество гибких элементов и длину отдельных элементов, которые требуются для решения симуляции:

Блок помещает один узел в основу и последующий конец вала. Эти узлы считаются фиксированными в осевом положении, потому что они представляют физические сущности вдоль оси вала. На схеме фиксированные узлы показаны красным цветом. Блок равномерно распределяет другие пять (_Nmin-2) внутренних узлов по длине вала. Затем он помещает гибкий элемент между каждой последовательной парой узлов.

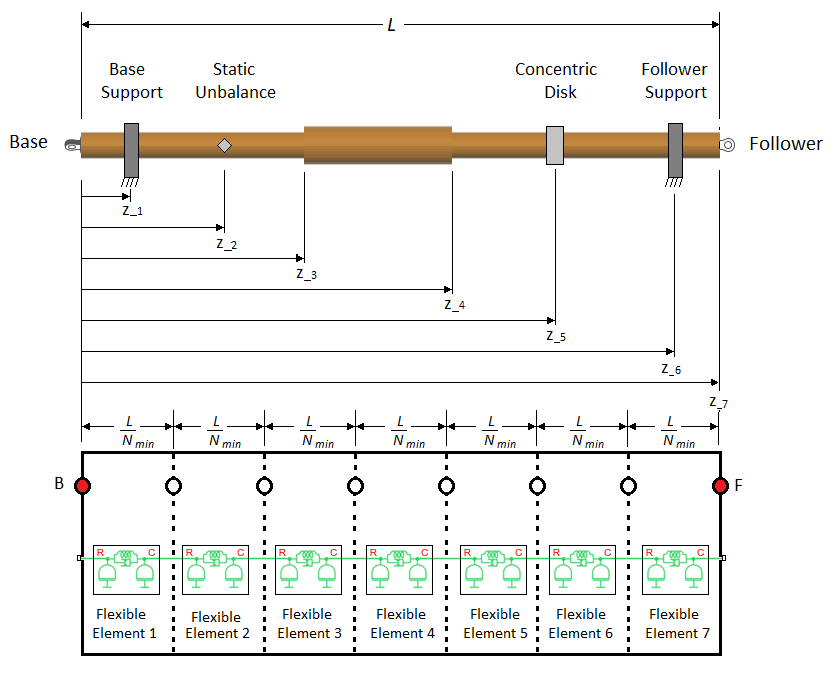
Для поддерживаемого концом, аксиально однородного вала, без статических дисбалансов или присоединенных концентрических дисков, в зависимости от других опций и значений, которые вы задаете, блок может быть в состоянии решить симуляцию, используя только _Nmin гибких элементов эквивалентной длины:

$l = \frac{L}{N_{\min}}$
Однако в большинстве случаев блок может решить симуляцию, только если добавляет более гибкие элементы.
Чтобы добавить более гибкие элементы, блок помещает фиксированные внутренние узлы в эти местоположения:
- Каждое место поддержки вала. Блок позволяет вам задать количество и расположение поддержек вала. Для вала в схеме предусмотрены поддержки на _z1 и _z6.
- Каждый статический дисбаланс. Для вала в схеме существует статический дисбаланс при _z2.
- Каждая твердая масса. Твердые массы являются концентрически присоединенными дисками или точечными массами. Для вала в схеме имеется жесткая масса, представленная в виде диска, на _z5.
- Каждый узел сегментов параметризации. Контуры параметризации являются расположениями вдоль аксиально неоднородного вала, где две соседние секции вала варьируются по жесткости, инерции или геометрии. Блок позволяет вам задать местоположения узлов сегментов параметризации. Для вала в схеме имеются узлы сегментов в _z3 и _z4.
  
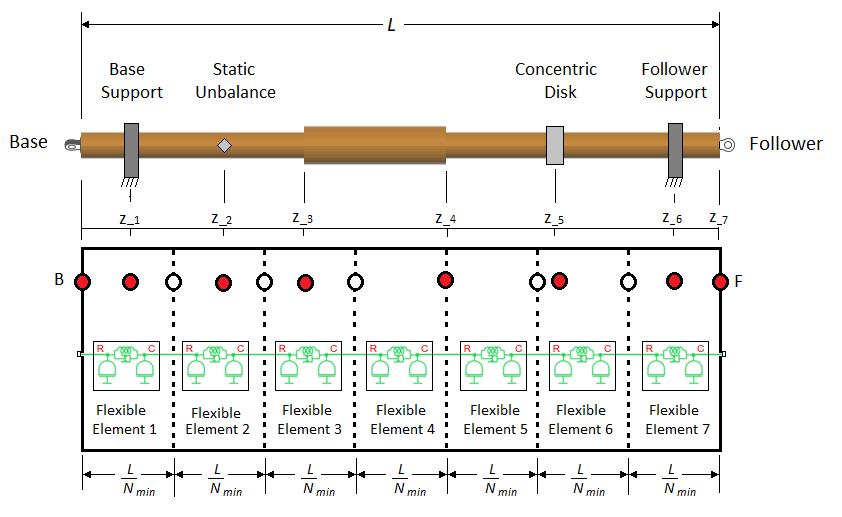
  Обратите внимание, что блок не добавил узел в _z4, потому что узел уже был добавлен на предыдущем шаге алгоритма. Однако теперь узел фиксирован, потому что он представляет физическую сущность вдоль длины вала.
Блок настраивает положения нефиксированных узлов между фиксированными узлами так, чтобы они были равномерно распределены.

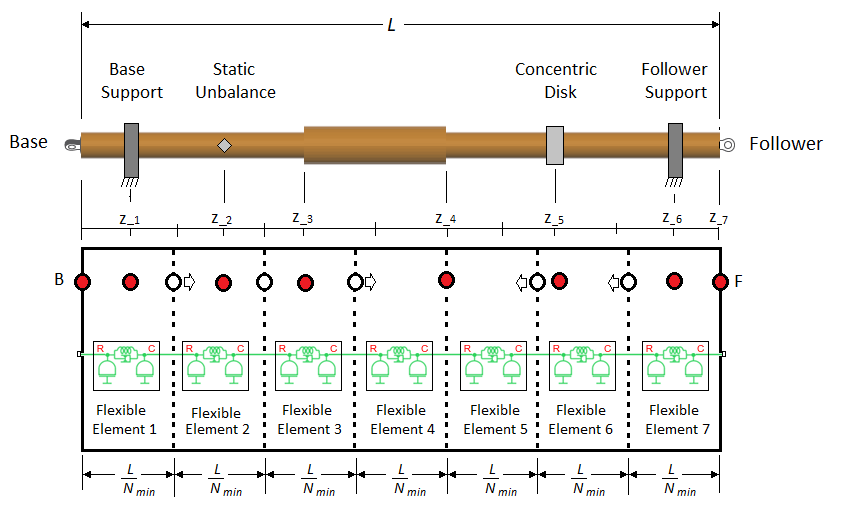
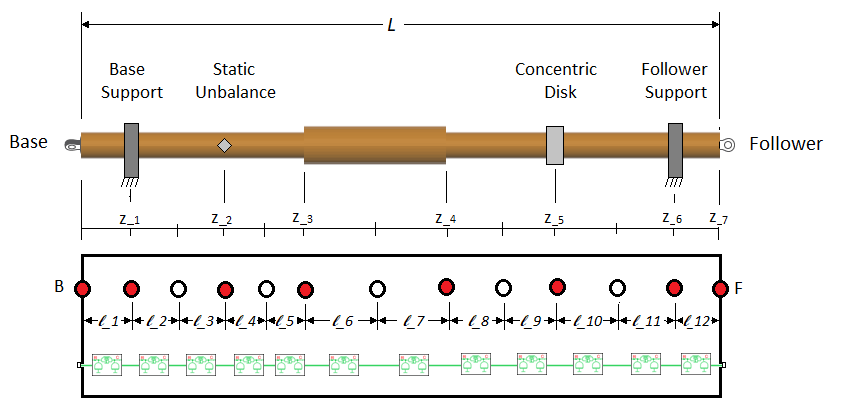
Наконец, блок помещает гибкие элементы между каждым узлом. Длина каждого гибкого элемента соответствует расстояниям между соседними узлами. Блок распределяет инерцию между гибкими элементами на основе длины отдельного элемента и соответствующей геометрии вала. В конечном счете, этот сложный вал представлен 12 гибкими элементами, с $l_{1} = z_{1}$ , $l_{2} = l_{3} = \frac{(z_{2} - z_{1})}{2}$ , $l_{4} = l_{5} = \frac{(z_{3} - z_{2})}{2}$ , $l_{6} = l_{7} = \frac{(z_{4} - z_{3})}{2}$ , $l_{8} = l_{9} = \frac{(z_{5} - z_{4})}{2}$ , $l_{10} = l_{11} = \frac{(z_{6} - z_{5})}{2}$ , и $l_{12} = z_{7} - z_{6}$ .

Если _Nmin достаточно велик, чтобы получить количество нефиксированных узлов, которое больше, чем количество фиксированных узлов, блок распределяет более одного нефиксированного узла между каждым набором соседних фиксированных узлов.

Размерности и свойства материала

Можно параметризовать модель кручения с помощью жесткости, k и полярного момента инерции, J или размерностей и свойств материала вала.

Жесткость и инерция для каждого элемента вычисляются из размерностей вала и свойств материала как:

$J_{p} = \frac{π}{32} (D^{4} - d^{4})$

$m = \frac{π}{4} (D^{2} - d^{2}) ρ l$

$J = \frac{m}{8} (D^{2} + d^{2}) = ρ l \cdot J p$

$k = J p \cdot \frac{G}{l}$

где:

_JP - полярный момент инерции вала в месте расположения гибкого элемента.
D - внешний диаметр вала в месте расположения гибкого элемента.
d - внутренний диаметр вала в месте расположения гибкого элемента. Для твердого вала, $d = 0$ . Для кольцевого вала, $d > 0$ .
$l$ - длина гибкого элемента.
m - масса вала в месте расположения гибкого элемента.
J - момент инерции вала в месте расположения гибкого элемента.
ρ - плотность материала вала.
G - модуль сдвига упругости материала вала.
k - вращательная жесткость гибкого элемента.

Демпфирование внутреннего материала

Для любой параметризации кручения внутреннее демпфирование материала определяется коэффициентом затухания, c, для модели с одним гибким элементом с эквивалентной крутящей жесткостью и инерцией. Коэффициент демпфирования тогда $2 \frac{c k}{ω_{N}}$ , где неповрежденная естественная частота $ω_{N} = \sqrt{\frac{2 k}{J}} .$ Демпфирующий крутящий момент, приложенный к отдельному гибкому элементу массива модели комкнутой массы, эквивалентен продукту коэффициента демпфирования и относительной скорости вращения этого гибкого элемента.

Модели изгиба

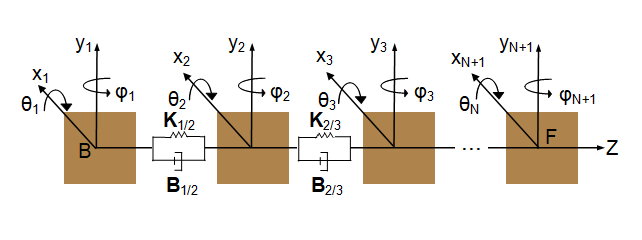
Геометрия вала, Поддержки Загрузки и рисунка Движения показов, как измерить:

Статический угол смещения дисбаланса, который является углом статического дисбаланса вокруг оси вала относительно оси x
Расстояния поддержки, жесткой массы и статического дисбаланса, относительно базового конца вала, B
Параметризация длин сегментов

На рисунке вал имеет три неподвижные поддержки:

_B1 - Поддержка конца основы
_I1 - Промежуточная поддержка
_F1 - Поддержка последующего конца

Вал имеет V поступательной скорости, W скорости вращения и прикладывает силы F и моменты M к поддержкам. Изогнутые стрелы и соглашения о знаках следуют правилу правой руки. Знаки физических сигналов, которые выводит блок, соответствуют стрелам, которые представляют силы, моменты и скорости вала, действующие на поддержки.

Векторные сигналы:

Сила, $F r = [F_{x B 1}, F_{y B 1}, F_{x I 1}, F_{y I 1}, F_{x F 1}, F_{y F 1}]$
Момент, $M = [M_{x B 1}, M_{y B 1}, M_{x I 1}, M_{y I 1}, M_{x F 1}, M_{y F 1}]$
Поступательная скорость, $V = [V_{x B 1}, V_{y B 1}, V_{x I 1}, V_{y I 1}, V_{x F 1}, V_{y F 1}]$
Скорость вращения, $M = [M_{x B 1}, M_{y B 1}, M_{x I 1}, M_{y I 1}, M_{x F 1}, M_{y F 1}]$

Если вал имеет две поддержки, каждый векторный сигнал имеет длину четыре. Сила, например, тогда $F r = [F_{x B 1}, F_{y B 1}, F_{x F 1}, F_{y F 1}]$ .

Если вал имеет четыре поддержки, каждый векторный сигнал имеет длину восемь. Сила, например, тогда $F r = [F_{x B 1}, F_{y B 1}, F_{x I 1}, F_{y I 1}, F_{x I 2}, F_{y I 2}, F_{x F 1}, F_{y F 1}]$ .

Геометрия вала, опорная загрузка и движение

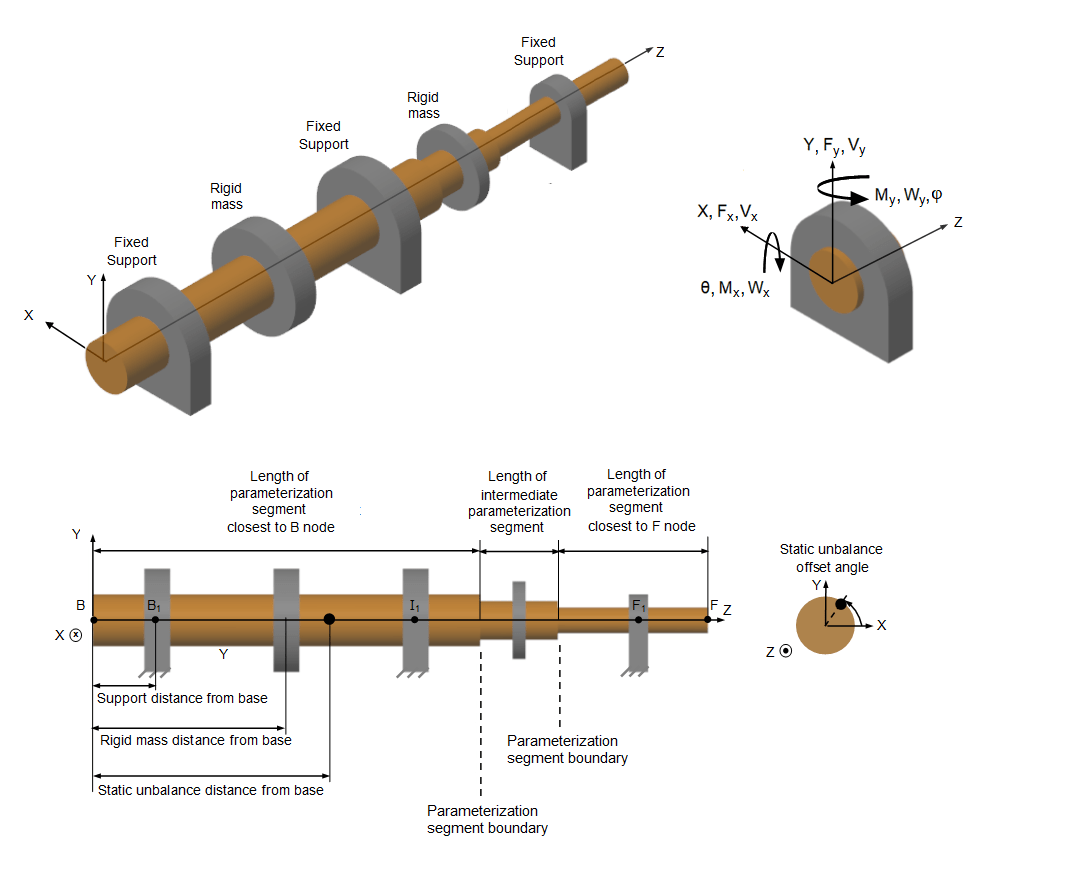
Модель изгиба Метод кусковой массы

Как и модель кручения, метод кусковой массы для модели изгиба дискретизирует распределенные непрерывные свойства вала в конечное число, N, гибких элементов. Гибкие элементы N соответствуют $N + 1$ кусковые инерции, соединенные последовательно демпфирующими и пружинными элементами. Однако для модели гибки каждая масса имеет четыре степени свободы: перемещение и вращение как в x, так и в y направлениях, перпендикулярных оси вала.

Объединенное массовое уравнение движения ^[1] является

$M \ddot{\vec{x}} + (B + G_{D i s k} Ω) \dot{\vec{x}} + (K + G_{D i s k} \dot{Ω}) \vec{x} = \vec{f} .$

где:

M является $4 (N + 1) \times 4 (N + 1)$ матрица, которая представляет массу вала.
B является $4 (N + 1) \times 4 (N + 1)$ матрица для внутреннего демпфирования и поддержки.
GDisk является $4 (N + 1) \times 4 (N + 1)$ матрица, которая учитывает дисковую гироскопию
Y - крутящая скорость вала во время симуляции.
K является $4 (N + 1) \times 4 (N + 1)$ матрица для жесткости пружины.
$\vec{x}$ является $4 (N + 1) \times 1$ вектор, который представляет степени свободы для всех узлов.
$\vec{f}$ является $4 (N + 1) \times 1$ вектор, который представляет внешние силы от приложения статического дисбаланса массы.

Уравнение для большой матрицы [4] является

$M = M_{1 / 2} + M_{2 / 3} + \dots M_{i / i + 1} + \dots M_{N / N + 1} + \sum^{} M_{d i s k, i},$

где:

$M_{i / (i + 1)}$ является большая матрица для индивидуума гибкого элемента. Для каждого гибкого элемента половина массы и момента инерции передается в узлы на обоих концах гибкого элемента. $M_{i / (i + 1)}$ матрица имеет ненулевые элементы в $(4 i - 3) : (4 i + 4)$ строки и $(4 i - 3) : (4 i + 4)$ столбцы:

$M_{i / (i + 1)} = [\begin{matrix} 0 \\ ⋱ \\ \frac{1}{2} m & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & \frac{1}{2} m & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & I_{d} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & I_{d} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1}{2} m & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{2} m & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & I_{d} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & I_{d} \\ ⋱ \\ 0 \end{matrix}],$
где:
- $l$ - длина гибкого элемента вдоль вала между внутренними узлами. Чтобы определить длину каждого гибкого элемента, блок использует алгоритм, который описан в Алгоритме Размещения Узла. Каждый гибкий элемент содержит две инерции. Каждая инерция имеет две поступательные степени свободы, две вращательные степени свободы и одну матрицу жесткости.
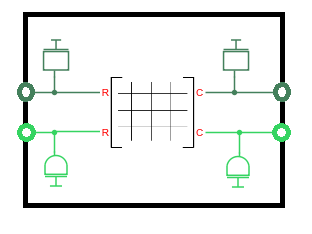
  Каждый гибкий элемент в эквивалентной физической модели для изгиба в XZ -плане (перемещение луча в X -направление и вращение вокруг оси Y) и в физической модели для изгиба в YZ -плане (перемещение луча в направлении Y и вращение вокруг оси X) затем содержит две массы, две инерции и матрицу жесткости
  
  Чтобы определить местоположения внутренних узлов, и, следовательно, количество и длины гибких элементов, блок использует тот же алгоритм размещения узлов, что и для модели кручения. Для получения дополнительной информации см. «Алгоритм размещения узлов».
- m - масса гибкого элемента. m зависит от внешнего, D и внутреннего, d, диаметров, плотности, ρ, вала и длины гибкого элемента, так что $m = (\frac{π}{4}) (D^{2} - d^{2}) ρ l$ .
- _Id масс полуэлемента момент инерции вокруг оси, перпендикулярной оси вала, зависит от массы, m, длины, $l$ и крутящий момент инерции, J, гибкого элемента, такого что $I_{d} = \frac{J}{4} + \frac{m}{6} {(\frac{l}{2})}^{2}$ .
$\sum^{} M_{d i s k, i}$ - суммированные большие матрицы твердых масс, концентрически присоединенные к валу.
Массовые свойства каждой твердой массы, которая концентрично присоединена к валу, добавляются к ближайшему узлу, $i$ , таким что

$M_{d i s k, i} ([(4 i - 3) : 4 i], [(4 i - 3) : 4 i]) = [\begin{matrix} M_{d i s k, i} & 0 & 0 & 0 \\ 0 & M_{d i s k, i} & 0 & 0 \\ 0 & 0 & I_{D, d i s k, i} & 0 \\ 0 & 0 & 0 & I_{D, d i s k, i} \end{matrix}],$
где _ID,disk,i - массовый диаметрический момент инерции вокруг оси, перпендикулярной валу, для жесткого диска, прикрепленного к i^th узел. Модель принимает, что диск тонкий, поэтому вал все еще может сгибаться с любой стороны осевого положения вместе с диском. Концентрическая масса точки $I_{D, d i s k, i} = 0$ .

Уравнение для демпфирующей матрицы

$B = α M + β K + B_{s u p p o r t},$

где:

α - постоянная демпфирования, пропорциональная массе.
β - коэффициент демпфирования, пропорциональный жесткости.
Bsupport - коэффициент демпфирования на каждой поддержке. Для поддержки в i^th узел, демпфирующая матрица, с точки зрения глобальных координат, является

$B_{s u p p o r t} ([(4 я - 3) : 4 я], [(4 я - 3) : 4 я]) = [\begin{matrix} b_{x x} & b_{x y} & 0 & 0 \\ b_{y x} & b_{y y} & 0 & 0 \\ 0 & 0 & b_{θ θ} & 0 \\ 0 & 0 & 0 & b_{φ φ} \end{matrix}],$
где:
- $[b_{x x} b_{x y} b_{y x} b_{y y}]$ - поступательное демпфирование поддержки.
- $[b_{θ θ} b_{φ φ}]$ - вращательное демпфирование поддержки.
$G_{d i s k, i}$ учитывает гироскопические эффекты любых концентрически присоединенных дисков и определяется как

$G_{d i s k, i} ([(4 i - 3) : 4 i], [(4 i - 3) : 4 i]) = [\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & Ω I_{P, d i s k, i} \\ 0 & 0 & - Ω I_{P, d i s k, i} & 0 \end{matrix}],$
где _IP,disk,i - массовый полярный момент инерции вокруг оси вала для диска, присоединенного к i^th узел. Масса полярного момента инерции для концентрической массы точки равна $I_{P, d i s k, i} = 0$ .

Уравнение для матрицы жесткости подшипника

$K = K_{1 / 2} + K_{2 / 3} + ... + K_{N / N + 1} + \sum^{} K_{support},$

где:

$K_{i / i + 1}$ - матрица жесткости для отдельного гибкого элемента вала. Матрица жесткости для $i^{t h}$ гибкий элемент вала, между i^th и ${(i + 1)}^{t h}$ узлы, имеет ненулевые элементы в $(4 i - 3) : (4 i + 4)$ строки и $(4 i - 3) : (4 i + 4)$ столбцы, такие что

$K_{i / i + 1} = \frac{2 E I}{l^{3}} [\begin{matrix} 0 \\ ⋱ \\ 6 & 0 & 0 & 3 l & - 6 & 0 & 0 & 3 l \\ 0 & 6 & - 3 l & 0 & 0 & - 6 & - 3 l & 0 \\ 0 & - 3 l & 2 l^{2} & 0 & 0 & 3 l & l^{2} & 0 \\ 3 l & 0 & 0 & 2 l^{2} & - 3 l & 0 & 0 & l^{2} \\ - 6 & 0 & 0 & - 3 l & 6 & 0 & 0 & - 3 l \\ 0 & - 6 & 3 l & 0 & 0 & 6 & 3 l & 0 \\ 0 & - 3 l & l^{2} & 0 & 0 & 3 l & 2 l^{2} & 0 \\ 3 l & 0 & 0 & l^{2} & - 3 l & 0 & 0 & 2 l^{2} \\ ⋱ \\ 0 \end{matrix}],$

где:
- $l$ - длина гибкого элемента.
- EI - жесткость вала.
Ksupport - жесткость на каждой поддержке. Для поддержки в i^th узел, матрица жесткости, с точки зрения глобальных координат,

$K_{s u p p o r t} ([(4 я - 3) : 4 я], [(4 я - 3) : 4 я]) = [\begin{matrix} k_{x x} & k_{x y} & 0 & 0 \\ k_{y x} & k_{y y} & 0 & 0 \\ 0 & 0 & k_{θ θ} & 0 \\ 0 & 0 & 0 & k_{φ φ} \end{matrix}],$
где:
- $[k_{x x} k_{x y} k_{y x} k_{y y}]$ - поддержка поступательная жесткость.
- $[k_{θ θ} k_{φ φ}]$ - жесткость вращения поддержки.

Матрица жесткости поддержки, _Ksupport, ненулевая, только если вы выбираете Bearing matrix или Speed-dependent bearing matrix для поддержки. Если вы выбираете Clamped тип монтажа, кинематические условия нулевого поворота и перемещения применяются к степеням свободы, соответствующим узлу поддержки (B1, I1, I2 или F1). Если вы выбираете Pinned тип монтирования, кинематические условия нулевого перевода применяются к поступательным степеням свободы, которые соответствуют узлу поддержки (B1, I1, I2 или F1).

Таблица включает граничные условия, применяемые к суженным узлам масс с поддержками.

Тип поддержки	Граничное условие для уравнения с единичной массой
`Clamped`	$x_{i} = 0, y_{i} = 0, θ_{i} = 0, φ_{i} = 0$
`Pinned`	$x_{i} = 0, y_{i} = 0$
`Bearing Matrix`	_Ksupport нетривиальна.
`Speed-dependent bearing matrix`	_Ksupport нетривиальна и зависит от скорости вращения вала. На каждом временном шаге _KSupport вычисляется как: $K_{S u p p o r t} (Ω) = l o o k u p (\| Ω_{R e f} \|, K_{S u p p o r t, R e f}, Ω, i n t e r p o l a t i o n = l i n e a r, e x t r a p o l a t i o n = n e a r e s t),$ где: _.Ref - скорость подшипника, заданная, в настройках Supports, для параметра Bearing speed [s1,...,sS]. Для каждой поддержки _KSupport,Ref зависимая от скорости подшипника поступательная жесткость, которую вы задаете в Supports настройках. Интерполяционная таблица использует линейную интерполяцию и ближайшую экстраполяцию для скорости вращения вала.

Матрица, которая представляет степени свободы для всех узлов, $\vec{x}$ , вычисляется таким образом, чтобы степени свободы для i^th и ${(i + 1)}^{t h}$ узлы

$\vec{x} = [\begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} ⋮ \\ \begin{matrix} x_{i} \\ y_{i} \\ θ_{i} \end{matrix} \\ φ_{i} \\ \begin{matrix} \begin{matrix} x_{i + 1} \\ y_{i + 1} \\ θ_{i + 1} \end{matrix} \\ φ_{i + 1} \\ ⋮ \end{matrix} \end{matrix} \end{matrix} \end{matrix} \end{matrix}] .$

Внешние силы из-за каждого статического дисбаланса массы прикладываются к ближайшему узлу. Усиление в $i^{t h}$ узел есть

${\vec{f}}_{4 (i - 1 : i - 2)} = [\begin{matrix} m ε_{j, o f f s e t} (Ω^{2}_{i} \cos (φ_{s h a f t, i} + φ_{o f f s e t, j}) + \frac{\partial Ω_{i}}{\partial t} \sin (φ_{s h a f t, i} + φ_{o f f s e t, j})) \\ m ε_{j, o f f s e t} (Ω^{2}_{i} \sin (φ_{s h a f t, i} + φ_{o f f s e t, j}) - \frac{\partial Ω_{i}}{\partial t} \cos (φ_{s h a f t, i} + φ_{o f f s e t, j})) \end{matrix}],$

где:

_mεj является j^thстатический дисбаланс, расположенный на i^thузел.
_{J i} - скорость вращения вала во время симуляции для i^th узел.
_{φshaft, i} - угол поворота скругленной массы кручения для i^th узел.

Метод изгиба модели Eigenmodes

Для метода собственных моделей блок уменьшает динамику изгиба от $4 (N + 1)$ степени свободы, которые предоставляет метод сгибающей модели с кусковой массой, для M степеней свободы, где M количество режимов.

Блок вычисляет свойства режима изгиба вала во время компиляции модели, затем решает модальные системы масса-пружина-демпфер во время симуляции модели.

Уменьшение степеней свободы в динамике модели и разделение вычислений на задачи во время компиляции и во время выполнения улучшает эффективность симуляции. Метод eigenmodes предполагает, что формы режима не влияют на демпфирование. Поэтому метод лучше всего подходит для моделей, которые включают ограниченное гироскопическое и поддерживающее демпфирование диска.

Во время компиляции блок вычисляет приблизительные демпфированные собственные модели с помощью следующих шагов:

Блок вычисляет матрицы, используя то же кусковое уравнение движения массы, которое он использует для метода сгибающей модели суженной массы:

$M \ddot{\vec{x}} + (B + G_{D i s k} Ω) \dot{\vec{x}} + (K + G_{D i s k} \dot{Ω}) \vec{x} = \vec{f} .$
Для получения дополнительной информации см. Раздел «Модель изгиба Метод кусковой массы».
При определении осевых местоположений узла для $\vec{x}$ , блок использует одну из двух изменений Алгоритма Размещения Узлов, который он использует для модели кручения и метода сгибания модели суженной массы. Изменение, которую использует блок, зависит от того, установлен ли параметр Bending mode determination в настройках Advanced Bending Simscape determined или к User defined.
Если для параметра Bending mode determination задано значение Simscape determined, вместо использования параметра Minimum number of flexible elements для _Nmin, как это делают методы кусковой массы, метод eigenmodes вычисляет _Nmin как

$N_{M i n, E i g} = r o u n d (\frac{L}{d z}),$
где:
- L - заданное значение в настройках Shaft для параметра Shaft length.
- dz - заданное значение в настройках Advanced Bending для параметра Shaft length increments for mode shape computations.
Чтобы вычислить m расшатанные собственные модели и собственные частоты, блок использует eigs функция. Уравнение принимает форму:
```
[H, λ] = eigs( sparse(K), sparse(M), mMax, 'smallestabs’ ),
```
где:
- H является $4 (N + 1) \times M$ матрица собственных векторов. Каждый столбец является собственной модой в $\vec{x}$ координаты.
- λ являются собственными значениями, которые являются квадратом собственных квот.
- _mMax - заданное значение в настройках Advanced Bending для параметра Limit number of modes.
Количество вычисленных собственных моделей, m, меньше _mMax, если:
- Существуют режимы с собственными частотами, которые превышают заданное значение, в настройках Advanced Bending для параметра Eigenfrequency upper limit. Блок отбрасывает эти режимы.
- Собственные значения не сходятся. Для получения дополнительной информации см. eigs.
Если для параметра Bending mode determination задано значение User definedблок вычисляет собственный вектор матрицу H из заданных значений, в настройках Advanced Bending, для этих параметров:
- X-direction mode shapes
- Y-direction mode shapes
- Shaft position
Чтобы определить осевые положения узла для $\vec{x}$ блок использует элементы, заданные для параметра Shaft position, в качестве основных узлов.
Чтобы вычислить модальное вращение, θ и φ, для каждого узла, блок использует gradient функция. Уравнения принимают форму:
```
θ = -gradient(Y direction mode shapes)
φ = gradient(X direction mode shapes)
```
Блок собирает X-direction mode shapes, Y-direction mode shapes и модальные повороты $\vec{x}$ координаты для каждого столбца H.
Блок вычисляет модальные матрицы, MModal, KModal, BModal, GModal, и _fModal, как:
$M_{M o d a l} = H^{T} M H$
$K_{M o d a l} = H^{T} K H$
$B_{M o d a l} = H^{T} B H$
$G_{M o d a l} = H^{T} G_{D i s k} H$
${\vec{f}}_{M o d a l} = H^{T} \vec{f}$
Несмотря на то, что блок вычисляет неослабленные собственные модели, H на шаге 1 модальная демпфирующая матрица, BModal и модальная гироскопическая матрица, GModal, могут моделировать световое демпфирование. Блок нормирует матрицы так, чтобы MModal были тождества матрицей.

Во время симуляции блок моделирует собственное уравнение движения:

$M_{M o d a l} \ddot{\vec{η}} + (B_{M o d a l} + G_{M o d a l} Ω) \dot{\vec{η}} + (K_{M o d a l} + G_{M o d a l} \dot{Ω}) \vec{η} = {\vec{f}}_{M o d a l},$

где модальные степени свободы, $\vec{η}$ , относятся к узлу степеням свободы путем:

$\vec{x} = H \vec{η}$

Скоростезависимый метод Eigenmodes

Жесткость поддержки и демпфирование поддержки изменяются, если в настройках Supports параметр типа монтажа для любого из поддержек установлен в Speed-dependent bearing matrix. Зависимые от скорости eigenmodes образцовые счета на эти эффекты, изменяя модальные свойства, H, BModal, GModal, KModal, и _fModal как скорость вала изменяются. MModal нормировано к тождествам матрице для всех скоростей вала, поэтому это не зависит от скорости вала.

Если вал имеет зависящие от скорости поддержки подшипника, то блок повторяет шаги метода режима изгиба для каждого элемента в векторе скорости вала. Элементы вектора вала являются заданными значениями, в настройках Supports, для параметра Bearing speed [s1,...,sS]. Во время симуляции модальная жесткость, демпфирование и принудительная величина регулируются на основе интерполяционных таблиц свойств в зависимости от скорости вала.

То есть блок моделирует собственное уравнение движения как:

$M_{M o d a l} \ddot{\vec{η}} + (B_{M o d a l} (Ω) + G_{M o d a l} (Ω) Ω) \dot{\vec{η}} + (K_{M o d a l} (Ω) + G_{M o d a l} (Ω) \dot{Ω}) \vec{η} = {\vec{f}}_{M o d a l} (Ω),$

где KModal, BModal и _fModal имеют форму:

$K_{M o d a l} (Ω) = l o o k u p (| Ω_{R e f} |, K_{M o d a l, R e f}, Ω, i n t e r p o l a t i o n = l i n e a r, e x t r a p o l a t i o n = n e a r e s t),$

$B_{M o d a l} (Ω) = l o o k u p (| Ω_{R e f} |, B_{M o d a l, R e f}, Ω, i n t e r p o l a t i o n = l i n e a r, e x t r a p o l a t i o n = n e a r e s t),$

$G_{M o d a l} (Ω) = l o o k u p (| Ω_{R e f} |, G_{M o d a l, R e f}, Ω, i n t e r p o l a t i o n = l i n e a r, e x t r a p o l a t i o n = n e a r e s t),$

${\vec{f}}_{M o d a l} (Ω) = l o o k u p (| Ω_{R e f} |, {\vec{f}}_{M o d a l, R e f}, Ω, i n t e r p o l a t i o n = l i n e a r, e x t r a p o l a t i o n = n e a r e s t),$

где:

_.Ref - заданное значение, в настройках Supports, для параметра Bearing speed [s1,...,sS].
KModal,Ref представляет собой таблицу модальных жесткостей при каждом
_BModal,Ref - таблица поддержки при каждом
_GModal,Ref - таблица дискового гироскопического демпфирования при каждом
fModal,Ref является таблицей модальных воздействий на каждый

Блок коррелирует подобие формы режима при различных значениях, _и при необходимости переупорядочивает режимы, так что каждая модальная степень свободы, $\vec{η}$ , имеет свойства, которые постепенно изменяются со скоростью вала.

Улучшите скорость симуляции или точность

Баланс между точностью симуляции и эффективностью зависит от N, количества гибких элементов, которые используются блоком для представления вала. Точность симуляции является мерой того, насколько результаты симуляции согласуются с математическими и эмпирическими моделями. Как правило, когда N увеличивается, также происходит и верность модели и точность симуляции. Однако вычислительная стоимость симуляции также коррелирует с N, и как только вычислительная стоимость увеличивается, эффективность уменьшается. И наоборот, когда N уменьшается, скорость симуляции увеличивается, но точность симуляции уменьшается.

Чтобы увеличить точность симуляции для метода кусковой массы для модели кручения или изгиба, увеличьте минимальное количество гибких элементов, _Nmin. Модель кручения с одним гибким элементом показывает собственную частоту кручения, которая близка к первой собственной частоте непрерывной модели распределенного параметра. Для большей точности можно выбрать 2, 4, 8 или более гибких элементов. Для примера четыре самых низких крутильных собственных требования представлены с точностью 0,1, 1,9, 1,6 и 5,3 процента, соответственно, моделью с 16 гибкими элементами.

Чтобы увеличить точность симуляции для метода eigenmodes к модели гибки:

Если симуляция со статической зависимостью собственной модели от скорости вращения, проверьте, что параметр Nominal shaft speed for bending modes близок к скорости симуляционного вала. Этот параметр может повлиять на результаты модели, если вы параметризоваете жесткий диск, прикрепленный к валу с большим моментом инерции массы вокруг оси вала или задаете любые зависящие от скорости поддержки матрицы подшипника.
Если симуляция с динамической зависимостью собственной модели от скорости вращения, проверьте, что в настройках Supports заданные значения для Bearing speed [s1,...,sS] охватывают диапазон скоростей вала симуляции или что насыщение жесткости поддержки и демпфирования при скоростях вала за пределами области значений является приемлемым приближением.
В настройках Advanced Bending уменьшите значение параметра Shaft length increments for mode shape computations. Уменьшение значения может увеличить точность модальных частот и форм.
Уменьшите демпфирование поддержки и полярный момент инерции диска вокруг оси вала. Simscape™ расчетов форм и частот режима перед симуляцией не учитывают это демпфирование.
Проверьте чувствительность к настройкам Advanced Bending, используя свои параметры в модели гибкого вала в примере Вал с кручением и поперечной гибкостью. Настройте параметры и используйте ссылки, представленные в примере, чтобы изучить, как значения влияют на частоты и формы собственной модели. Скорректируйте значения параметров в модели соответственно.
Увеличьте значения параметров Eigenfrequency upper limit и Limit number of modes. Самая высокая модальная частота в симуляции должна быть значительно больше, чем частота вращения вала.

Допущения и ограничения

Распределенная параметром модель непрерывного кручения вала аппроксимируется конечным числом, N, кусковых масс.
Вращение вала и гибкость кручения приводят к изгибу вала, но изгиб не влияет на вращение вала и гибкость кручения.
Твердые точечные массы или диски, прикрепленные к валу, имеют тонкие длины, параллельные оси вала.
Для модели изгиба собственных мод демпфирование не влияет на собственные частоты.
Изгиб вала не передается между блоками Flexible Shaft.
Относительно длины вала наружный диаметр вала невелик.
Относительно длины вала отклонение изгиба невелико.
Статические дисбалансы массы являются единственными внешними возбуждающими нагрузками, изгибающими вал.
Поддержки вала неподвижны.
Рассматриваются гироскопические эффекты жестких дисков; гироскопические эффекты самого вала пренебрегают.
Статический дисбаланс масс в методе собственных моделей использует скорость вращения в средней точке вала.
Если вал моделирует только кручение и использует опции параметризации By stiffness and inertia или By segment stiffness and inertia, то блок использует только две поддержки, по одной на B и F концах.

Порты

Выход

расширить все

`Fr` - Усилие на опоры подшипника
физический сигнал

Выход физического сигнала, сопоставленный с силой, которую вал оказывает на поддержки подшипника.

Зависимости

Этот порт видим, если в настройках Shaft параметр Model bending равен On. Для получения дополнительной информации смотрите Модель изгиба.

`M` - Момент на опорах подшипника
физический сигнал

Выход физического сигнала сопоставлен с моментом, когда вал воздействует на поддержки подшипника.

Зависимости

`V` - Поступательная скорость вала
физический сигнал

Выход физического сигнала сопоставлен с поступательной скоростью вала у подшипника поддержек.

Зависимости

`W` - Угловая скорость вала
физический сигнал

Выход физического сигнала сопоставлен с скоростью вращения вала у подшипника поддержек.

Зависимости

Сохранение

расширить все

`B` - Основа
вращательный механический

Вращательный порт сопоставлен с основой вала.

`F` - Последующий
вращательный механический

Вращательный порт сопоставлен с последующим валом.

Параметры

расширить все

Вал

Для определенных параметров в настройках Shaft выбранная вами опция влияет на видимость:

Другие параметры в настройках Shaft.
Параметры в настройках Torsion.
Supports настройки и параметры.
Bending настройки
Advanced Bending настройки
Эти выходные порты:
- Fr
- M
- V
- W

Таблица показывает, как опции, которые вы выбираете для настроек Shaft, влияют на видимость других параметров в настройках Shaft. Чтобы узнать, как считать таблицу, см. «Параметры».

Зависимости параметров вала

Параметры и значения настройки вала
Model bending
`Off`						`On`
Minimum number of flexible elements						Minimum number of flexible elements
Parameterization						Parameterization
`By stiffness and inertia`	`By material and geometry`		`By segment stiffness and inertia`	`By material and segment geometry`		`By stiffness and inertia`	`By material and geometry`		`By segment stiffness and inertia`	`By material and segment geometry`
`By stiffness and inertia`	Shaft Length		`By segment stiffness and inertia`	Segment lengths [B,...,F]		Shaft Length	Shaft Length		Segment lengths [B,...,F]	Segment lengths [B,...,F]
Torsional stiffness			Segment torsional stiffness [B,...,F]			Torsional stiffness			Segment torsional stiffness [B,...,F]
Torsional inertia			Segment torsional inertia [B,...,F]			Torsional inertia			Segment torsional inertia [B,...,F]
						Bending rigidity			<reservedrangesplaceholder1> <reservedrangesplaceholder0>
	Material density			Material density		Linear density	Material density		<reservedrangesplaceholder1> <reservedrangesplaceholder0>	Material density
	Shear modulus			Shear modulus			Shear modulus			Shear modulus
	Shear modulus			Shear modulus			Young's modulus			Young's modulus
	Shaft geometry			Shaft geometry			Shaft geometry			Shaft geometry
	`Solid`	`Annular`		`Solid`	`Annular`		`Solid`	`Annular`		`Solid`	`Annular`
	Shaft outer diameter	Shaft outer diameter		Segment outer diameter [B,...,F]	Segment outer diameter [B,...,F]		Shaft outer diameter	Shaft outer diameter		Segment outer diameter [B,...,F]	Segment outer diameter [B,...,F]
	Shaft outer diameter	Shaft inner diameter		Segment outer diameter [B,...,F]	Segment inner diameter [B,...,F]		Shaft outer diameter	Shaft inner diameter		Segment outer diameter [B,...,F]	Segment inner diameter [B,...,F]

`Model bending` - опция модели изгиба
`Off` (по умолчанию) | `On`

Опция для моделирования изгиба вала.

Зависимости

На эти параметры, настройки и порты влияет параметр Model bending.

Для параметров Shaft видимость зависимых параметров приведена в таблице «Зависимости параметра вала».
В настройках Torsion:
- Параметр Viscous friction coefficients at base (B) and follower (F) видим, если в настройках Shaft Model bending установлено на Off и Parameterization установлено на By stiffness and inertia или By segment stiffness and inertia.
- Параметр Viscous friction coefficients at each support [B1,...,F1] видим, если в настройках Shaft достигается одно из следующих условий:
  - Model bending установлено на On.
  - Model bending установлено на Off и Parameterization установлено на By material and geometry или By material and segment geometry.
Эти настройки доступны, только если Model bending задано значение On:
- Supports
- Bending
- Advanced bending
Эти порты доступны, только если Model bending задано значение On:
- Fr
- M
- V
- W

`Minimum number of flexible elements` - Минимальное количество гибких элементов
`1` (по умолчанию) | положительное целое число

Минимальное количество гибких элементов, _Nmin, для приближения.

Возможно, что гибкие элементы имеют разную длину или что моделируемое количество гибких элементов, N, больше _Nmin. Для получения дополнительной информации см. «Алгоритм размещения узлов».

Большее количество гибких элементов, N, увеличивает точность модели, но снижает эффективность симуляции. Модель с одним гибким элементом (N = 1) показывает собственную частоту кручения, которая близка к первой собственной частоте непрерывной модели распределенного параметра.

Если точность модели важнее эффективности, выберите 2, 4, 8 или более гибких элементов. Для примера четыре самые низкие собственные частоты кручения представлены с точностью 0,1, 1,9, 1,6 и 5,3 процента, соответственно, моделью с 16 гибкими элементами. Как правило, для точного моделирования динамики изгиба требуется больше гибких элементов, чем для точного моделирования динамики кручения.

Для получения дополнительной информации смотрите Улучшить скорость симуляции или Точность.

`Parameterization` - Метод параметризации
`By stiffness and inertia` (по умолчанию) | `By material and geometry` | `By segment stiffness and inertia` | `By material and segment geometry`

Метод параметризации. Можно смоделировать однородный вал или тот, который является аксиально неоднородным для любого из следующих атрибутов:

Кручение жесткости
Инерция кручения
Жесткость при изгибе
Плотность
Модуль сдвига
Модуль Янга
Внешний диаметр
Внутренний диаметр

Опции параметризации для однородной модели вала:

By stiffness and inertia - Задайте крутящую жесткость и инерцию, а также плотность на единицу длины вала. Для модели изгиба также задайте жесткость изгиба и длину вала.
By material and geometry - Задайте длину и осевую геометрию поперечного сечения, с точки зрения внутреннего и внешнего диаметров вала. Для материала вала задайте модуль плотности и сдвига. Для модели изгиба также задайте модуль Юнга для материала вала.

Опции параметризации для аксиально неоднородной модели вала:

By segment stiffness and inertia - Для каждого сегмента вала задайте крутящую жесткость, инерцию кручения и плотность на единицу длины. Для модели изгиба также укажите жесткость и длину изгиба для каждого сегмента.
By material and segment geometry - Для каждого сегмента вала задайте длину и осевую геометрию поперечного сечения с точки зрения внутреннего и внешнего диаметров. Для материала вала задайте модуль плотности и сдвига. Для модели изгиба также задайте модуль Юнга для материала вала.

Зависимости

Каждая опция Parameterization влияет на видимость:

Зависимые параметры в настройках Shaft. Для получения дополнительной информации см. «Зависимости параметра вала».
Зависимые параметры в настройках Torsion:
- Параметр Viscous friction coefficients at base (B) and follower (F) видим, если в настройках Shaft Model bending установлено на Off и Parameterization установлено на By stiffness and inertia или By segment stiffness and inertia.
- Параметр Viscous friction coefficients at each support [B1,...,F1] видим, если в настройках Shaft достигается одно из следующих условий:
  - Model bending установлено на On.
  - Model bending установлено на Off и Parameterization установлено на By material and geometry или By material and segment geometry.
Настройки Supports. Когда параметр Model bending установлен в Offнастройки Supports видны, когда параметру Parameterization задано значение By material and geometry или By material and segment geometry.

`Shaft length` - Длина вала
`1` `m` (по умолчанию) | положительная скалярная величина

Длина вала.

Зависимости

Этот параметр видим, когда достигается одно из следующих условий:

Model bending установлено на Off и Parameterization установлено на By material and geometry.
Model bending установлено на On и Parameterization установлено на By material and geometry или By stiffness and inertia.

Для получения дополнительной информации о том, как другие параметры влияют на видимость этого параметра, см. «Зависимости параметра вала».

`Segment lengths [B,...,F]` - Длина каждого сегмента вала
`[1, .5, .25]` (по умолчанию) | вектор

Длина каждого сегмента вала, который вал разделен на продольные для моделирования аксиально неоднородного вала. Количество элементов в векторе равно количеству сегментов, которые вы используете для моделирования неоднородного вала. Порядок элементов в векторе соответствует порядку сегментов относительно B, базового конца вала.

Зависимости

Этот параметр видим, когда достигается одно из следующих условий:

Parameterization установлено на By material and segment geometry.
Model bending установлено на On и Parameterization установлено на By segment stiffness and inertia.

`Torsional stiffness` - Жесткость материала
`2e5` `N*m/rad` (по умолчанию) | положительная скалярная величина

Крутящий момент на радиальный поворот вала.

Зависимости

Этот параметр видим, когда Parameterization установлено на By stiffness and inertia.

`Segment torsional stiffness [B,...,F]` - Жесткость материала для каждого сегмента вала
`[400000, 200000, 100000]` `N*m/rad` (по умолчанию) | положительный вектор

Крутящий момент на радиан для каждого сегмента вала. Количество элементов в векторе должно совпадать с количеством элементов, заданным для параметра Segment lengths [B,...,F]. Порядок элементов в векторе соответствует порядку сегментов относительно B, базового конца вала.

Зависимости

Этот параметр видим, когда Parameterization установлено на By segment stiffness and inertia.

`Torsional Inertia` - Полярный момент инерции
`0.02` `kg*m^2` (по умолчанию) | положительная скалярная величина

Способность вала противостоять крутящему ускорению.

Зависимости

Этот параметр видим, когда Parameterization установлено на By stiffness and inertia.

`Segment torsional inertia [B,...,F]` - Полярный момент инерции для каждого сегмента вала
`[.025, .02, .015]` `kg*m^2` (по умолчанию) | положительный вектор

Способность каждого сегмента вала противостоять ускорению кручения. Количество элементов в векторе должно совпадать с количеством элементов, заданным для параметра Segment lengths [B,...,F]. Порядок элементов в векторе соответствует порядку сегментов относительно, B, базового конца вала.

Зависимости

Этот параметр видим, когда Parameterization установлено на By segment stiffness and inertia.

`Bending rigidity` - Жесткость изгиба
`5e5` `m^4*Pa` (по умолчанию) | положительная скалярная величина

Жесткость изгиба материала вала.

Зависимости

Этот параметр видим, когда Model bending установлено на On и Parameterization установлено на By stiffness and inertia.

`Segment bending rigidity [B,...,F]` - Жесткость изгиба каждого сегмента
`[600000, 500000, 400000]` `m^4*Pa` (по умолчанию) | положительный вектор

Жесткость изгиба для материала каждого последовательного сегмента вала. Количество элементов в векторе должно совпадать с количеством элементов, заданным для параметра Segment lengths [B,...,F]. Порядок элементов в векторе соответствует порядку сегментов относительно B, базового конца вала.

Зависимости

Этот параметр видим, когда Model bending установлено на On и Parameterization установлено на By segment stiffness and inertia.

`Linear density` - Плотность на единицу длины
`19` `kg/m` (по умолчанию) | положительная скалярная величина

Плотность материала вала на единицу длины вала.

Зависимости

Этот параметр видим, когда Parameterization установлено на By stiffness and inertia.

`Segment linear density [B,...,F]` - Плотность на единицу длины для каждого сегмента
`[20, 19, 18]` `kg/m` (по умолчанию) | положительный вектор

Плотность материала вала на единицу длины каждого сегмента вала. Количество элементов в векторе должно совпадать с количеством элементов, заданным для параметра Segment lengths [B,...,F]. Порядок элементов в векторе соответствует порядку сегментов относительно B, базового конца вала.

Зависимости

Этот параметр видим, когда Parameterization установлено на By segment stiffness and inertia.

`Material density` - Плотность материала
`7.8e3` `kg/m^3` (по умолчанию) | положительная скалярная величина

Плотность материала вала.

Зависимости

Этот параметр видим, когда Parameterization установлено на By material and geometry или By material and segment geometry.

`Shear modulus` - Модуль сдвига
`7.93e9` `Pa` (по умолчанию) | положительная скалярная величина

Модуль сдвига для материала вала.

Зависимости

Этот параметр видим, когда Parameterization установлено на By material and geometry или By material and segment geometry.

`Young's modulus` - Модуль Юнга
`200e9` `Pa` (по умолчанию) | положительная скалярная величина

Модуль Янга для материала.

Зависимости

Этот параметр видим, когда Model bending установлено на On и Parameterization установлено на By material and geometry или By material and segment geometry.

`Shaft geometry` - Геометрия поперечного сечения
`Solid` (по умолчанию) | `Annular`

Геометрия поперечного сечения по длине вала. Если вал или сегменты вала являются полыми, выберите Annular. В противном случае выберите Solid.

Зависимости

Этот параметр видим, когда Parameterization установлено на By material and geometry или By material and segment geometry.

`Shaft outer diameter` - Наружный диаметр вала
`0.075` `m` (по умолчанию) | положительная скалярная величина

Внешний диаметр вала.

Зависимости

Этот параметр видим, когда Parameterization установлено на By material and geometry.

`Segment outer diameter [B,...,F]` - Наружный диаметр для каждого сегмента вала
`[.085, .075, .065]` `m` (по умолчанию) | положительный вектор

Наружный диаметр каждого сегмента вала. Количество элементов в векторе должно совпадать с количеством элементов, заданным для параметра Segment lengths [B,...,F]. Порядок элементов в векторе соответствует порядку сегментов относительно B, базового конца вала.

Зависимости

Этот параметр видим, когда Parameterization установлено на By material and segment geometry.

`Shaft inner diameter` - Внутренний диаметр вала
`0.05` `m` (по умолчанию) | позитвенный скаляр

Внутренний диаметр кольцевого вала. Значение должно быть меньше значения, заданного для параметра Shaft outer diameter.

Зависимости

Этот параметр видим, когда Parameterization установлено на By material and geometry и Shaft geometry установлено на Annular.

`Segment inner diameter [B,...,F]` - Внутренний диаметр для каждого сегмента вала
`[.055, .05, .045]` `m` (по умолчанию) | вектор

Внутренние диаметры сегментов вала. Количество элементов в векторе должно совпадать с количеством элементов, заданным для параметра Segment lengths [B,...,F]. Порядок элементов в векторе соответствует порядку сегментов относительно B, базового конца вала. Каждое значение должно быть меньше, чем соответствующее значение, заданное для параметра Segment outer diameter [B,...,F]. Если сегмент вала является твердым, задайте 0 для соответствующего векторного элемента. По крайней мере, один элемент в векторе должен быть положительным.

Зависимости

Этот параметр видим, когда Parameterization установлено на By material and segment geometry и Shaft geometry установлено на Annular.

Скрученность

`Damping ratio from internal losses` - коэффициент затухания материала
`0.01` (по умолчанию) | положительная скалярная величина

Коэффициент затухания материала.

`Viscous friction coefficients at base (B) and follower (F)` - Коэффициенты вязкого трения
`[0, 0]` `N*m/(rad/s)` (по умолчанию) | неотрицательный вектор

Коэффициенты вязкого трения в основе, B и последующем, F, концах вала. Вектор должен содержать два элемента.

Зависимости

Этот параметр видим, если в настройках Shaft Model bending установлено на Off и Parameterization установлено на By stiffness and inertia или By segment stiffness and inertia.

`Viscous friction coefficients at each support [B1,...,F1]` - Коэффициенты вязкого трения
`[0, 0]` `N*m/(rad/s)` (по умолчанию) | неотрицательный вектор

Коэффициенты вязкого трения на каждой поддержке. Количество элементов в векторе должно совпадать с количеством, заданным в настройках Supports для параметра Number of supports. Порядок элементов должен соответствовать последовательному положению каждого опорного B, базового конца вала.

Зависимости

Этот параметр видим, если в настройках Shaft достигается одно из следующих условий:

Model bending установлено на On.
Model bending установлено на Off и Parameterization установлено на By material and geometry или By material and segment geometry.

`Initial shaft torsional deflection` - Начальное кручение вала
`0` `rad` (по умолчанию) | неотрицательной скаляром

Угловое отклонение вала в начале симуляции.

Положительное начальное отклонение приводит к положительному вращению B, базового конца вала, относительно F, последующего конца вала.

`Initial shaft angular velocity` - Начальная скорость вращения
`0` `rpm` (по умолчанию) | неотрицательной скаляром

Скорость вращения вала в начале симуляции.

Поддержки

Настройки Supports видны, если в настройках Shaft выполнено одно из следующих условий:

Model bending установлено на Off и Parameterization установлено на By material and geometry или By material and segment geometry.
Для этого условия видны только эти параметры в настройках Supports:
- Number of supports
- Support locations relative to base (B)
Model bending установлено на On.
Видимость настроек Supports зависит от значений нескольких параметров в настройках Supports.

В настройках Supports, если параметр Number of supports установлен на 2видны только типы монтажа и зависимые параметры для B1 и F1 поддержек. B1 поддержки является поддержкой, которая находится ближе всего к B, основанию вала. F1 поддержки является поддержкой, которая наиболее близка к F, последующему концу вала. Если Number of supports задано значение, больше 2тип монтажа и зависимые параметры открыты для промежуточных поддержек, _IN, где N количество промежуточных поддержек. Для примера, для 3 поддержки, тип монтажа и зависимые параметры для B1, I1 и F1 поддержки являются открытыми.

В этих таблицах показаны зависимости параметров для Lumped Mass и Eigenmodes методы анализа гибочных вибраций для каждого типа монтажа. Параметры видны для B1 и F1 поддержек и для любых промежуточных поддержек, I1 и I2, которые вы задаете. Имена зависимых параметров префиксируются именем соответствующей поддержки. Для примера, для поддержки B1, зависимый Rotational damping [xx,yy] параметра называется Base (B1) rotational damping [xx,yy]. Префиксы параметров:

Base (B1)
Intermediate (I1)
Intermediate (I2)
Follower (F1)

Зависимости параметров типа монтажа

Supports типов монтажа и зависимых параметров
`Clamped`	`Pinned`	`Free`	`Bearing matrix`	`Speed-dependent bearing matrix`
-	Rotational damping [xx,yy]	Rotational damping [xx,yy]	Rotational damping [xx,yy]	Rotational damping [xx,yy]
			Translational damping [xx,xy,yx,yy]	Speed-dependent translational damping [xx1,xy1, yx1,yy1;...xxS,xyS,yxS,yyS]
			Rotational stiffness [xx,yy]	Rotational stiffness [xx,yy]
			Translational stiffness [xx,xy,yx,yy]	Speed-dependent translational stiffness [xx1,xy1,yx1, yy1;...xxS,xyS,yxS,yyS]
			Translational stiffness [xx,xy,yx,yy]	Bearing speed [s1,…,sS]

`Number of supports` - Количество поддержек
`2` (по умолчанию) | `3` | `4`

Количество поддержек вала.

Зависимости

Этот параметр видим, если в настройках Shaft достигается одно из следующих условий:

Model bending установлено на Off и Parameterization установлено на By material and geometry или By material and segment geometry
Model bending установлено на On.

Если для этого параметра задано значение:

2 - Параметры для B1 и F1 поддержек открыты. B1 поддержки является поддержкой, которая ближе всего B к основанию вала. F1 поддержки является поддержкой, которая наиболее близка к F, последующему концу вала.
3 - Параметры для B1, I1 и F1 поддержек открыты.
4 - Параметры для B1, I1, I2 и F1 поддержек открыты.

`Support locations relative to base (B)` - Места оказания поддержки
`[0, 1]` `m` (по умолчанию) | неотрицательный вектор увеличения

Опорные положения относительно B, базового конца вала. Количество элементов должно совпадать с количеством, заданным для параметра Number of supports. Порядок элементов соответствует последовательному положению каждой поддержки относительно базового конца вала. Наибольшее значение должно быть не больше длины вала. Для модели сегментированного вала длина вала равна сумме отдельных длин сегментов.

Зависимости

Этот параметр видим, если в настройках Shaft достигается одно из следующих условий:

Model bending установлено на Off и Parameterization установлено на By material and geometry или By material and segment geometry
Model bending установлено на On.

`Base (B1) mounting type` - Поддержка B1 монтажа
`Clamped` (по умолчанию) | `Pinned` | `Free` | `Bearing matrix` | `Speed-dependent bearing matrix`

Тип крепления к основанию вала.

Зависимости

Этот параметр видим, когда в настройках Shaft параметр Model bending равен On. Для получения дополнительной информации см. «Зависимости параметра вала».

Установка этого параметра на Pinned, Free, Bearing matrix, или Speed-dependent bearing matrix отображает связанные параметры. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Base (B1) rotational damping [xx,yy]` - Поддержка B1 вращательного демпфирования
`[1e3, 1e3]` `N*m/(rad/s)` (по умолчанию) | вектор

Вращательное демпфирование для поддержки B1. B1 - поддержка, которая ближе всего к B, основание вала. Элементами двухэлементного вектора являются:

xx - Демпфирование вокруг оси x -отверстие
yy - Демпфирование вокруг оси y -отверстие

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support Base (B1) mounting type установлено на Pinned, Free, Bearing matrix, или Speed-dependent bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Base (B1) translational damping [xx,xy,yx,yy]` - Поддержка B1 поступательное демпфирование
`[2e4, -4.4e4, -4.4e4, 3.5e5]` `N/(m/s)` (по умолчанию) | вектор

Поступательное демпфирование для поддержки B1. Элементами вектора с четырьмя элементами являются:

xx - Демпфирование в направлении x -оси
xy - Демпфирование в направлении x -оси, связанное с движением в направлении y -оси
yx - Демпфирование в направлении y -оси, связанное с движением в направлении x -оси
yy - Демпфирование в направлении y -оси

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support Base (B1) mounting type установлено на Bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Base (B1) speed-dependent translational damping [xx1,xy1,yx1,yy1;...xxS,xyS,yxS,yyS]` - Поддержка B1 зависимости от скорости поступательного демпфирования
`[2e4, -4.4e4, -4.4e4, 3.5e5; 1e4, -2.5e4, -2.5e4, 1.4e5; 5e3, -1.0e4, -1.0e4, 2.0e4]` `N/(m/s)` (по умолчанию) | матрица

Зависящее от скорости поступательное демпфирование для поддержки B1. Количество строк в матрице должно равняться количеству элементов в векторе, заданном для параметра Bearing speed [s1, … sS]. Каждая строка содержит четыре элемента:

_xxs - Демпфирование в направлении x -оси в s^th скорость
_xys - Демпфирование в направлении x -оси, связанное с движением в направлении y -оси в s^th скорость
_yxs - Демпфирование в направлении y -оси, связанное с движением в направлении x -оси в s^th скорость
_yys - Демпфирование в направлении y -оси в s^th скорость

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support Base (B1) mounting type установлено на Speed-dependent bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Base (B1) rotational stiffness [xx,yy]` - Поддержка B1 вращательная жесткость
`[1e4, 1e4]` `N*m/rad` (по умолчанию) | неотрицательный вектор

Вращательная жесткость для поддержки B1. Элементами двухэлементного вектора являются:

xx - Жесткость вокруг оси x -отверстие
yy - Жесткость вокруг оси y -отверстие

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support Base (B1) mounting type установлено на Bearing matrix или Speed-dependent bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Base (B1) translational stiffness [xx,xy,yx,yy]` - Поддержка B1 поступательная жесткость
`[1e6, -2e5, -3e5, 5e]` `N/m` (по умолчанию) | вектор

Поступательная жесткость для поддержки B1. Элементами вектора с четырьмя элементами являются:

xx - Жесткость в x -осевом направлении
xy - Жесткость в направлении x -оси, связанная с движением в направлении y -оси
yx - Жесткость в направлении y -оси, связанная с движением в направлении x -оси
yy - Жесткость в y -осевом направлении

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support Base (B1) mounting type установлено на Bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Base (B1) speed-dependent translational stiffness [xx1,xy1,yx1,yy1;...xxS,xyS,yxS,yyS]` - Поддержка B1 зависимости от скорости поступательной жесткости
`[1e6, -6e5, -3.5e6, 8e6; 1e6, -2e5, -3.0e6, 5e6; 1e6, -5e4, -2.5e6, 3e6]` `N/m` (по умолчанию) | матрица

Зависимая от скорости поступательная жесткость для поддержки B1. Количество строк в матрице должно равняться количеству элементов в векторе, заданном для параметра Bearing speed [s1, … sS]. Каждая строка содержит четыре элемента:

_xxs - Жесткость в направлении x -оси в s^th скорость
_xys - Жесткость в направлении x -оси, связанная с движением в направлении y -оси в s^th скорость
_yxs - Жесткость в направлении y -оси, связанная с движением в направлении x -оси в s^th скорость
_yys - Жесткость в направлении y -оси в s^th скорость

Все xx и yy значения жесткости должны быть положительными. Все xy и yx значения должны быть нулем или ненулевыми на всех скоростях.

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support Base (B1) mounting type установлено на Speed-dependent bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Intermediate (I1) mounting type` - Поддержка I1 монтажа
`Clamped` (по умолчанию) | `Pinned` | `Free` | `Bearing matrix` | `Speed-dependent bearing matrix`

Тип монтажа на I1 поддержки. Поддержка I1 является ближайшей промежуточной поддержкой поддержки B1.

Зависимости

Этот параметр видим, когда оба из этих условий выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Supports Number of supports установлено на 3 или 4.

`Intermediate (I1) rotational damping [xx,yy]` - Поддержка I1 вращательного демпфирования
`[1e3, 1e3]` `N*m/(rad/s)` (по умолчанию) | вектор

Вращательное демпфирование для поддержки I1. Элементами двухэлементного вектора являются:

xx - Демпфирование вокруг оси x -отверстие
yy - Демпфирование вокруг оси y -отверстие

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support:
- Number of supports установлено на 3 или 4.
- Intermediate (I1) mounting type установлено на Pinned, Free, Bearing matrix, или Speed-dependent bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Intermediate (I1) translational damping [xx,xy,yx,yy]` - Поддержка I1 поступательное демпфирование
`[2e4, -4.4e4, -4.4e4, 3.5e5]` `N/(m/s)` (по умолчанию) | вектор

Поступательное демпфирование для поддержки I1. Элементами вектора с четырьмя элементами являются:

xx - Демпфирование в направлении x -оси
xy - Демпфирование в направлении x -оси, связанное с движением в направлении y -оси
yx - Демпфирование в направлении y -оси, связанное с движением в направлении x -оси
yy - Демпфирование в направлении y -оси

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support:
- Number of supports установлено на 3 или 4.
- Intermediate (I1) mounting type установлено на Bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Intermediate (I1) speed-dependent translational damping [xx1,xy1,yx1,yy1;...xxsS,xyS,yxS,yyS]` - Поддержка I1 зависимости от скорости поступательного демпфирования
`[2e4, -4.4e4, -4.4e4, 3.5e5; 1e4, -2.5e4, -2.5e4, 1.4e5; 5e3, -1.0e4, -1.0e4, 2.0e4]` `N/(m/s)` (по умолчанию) | матрица

Зависящее от скорости поступательное демпфирование для поддержки I1. Количество строк в матрице должно равняться количеству элементов в векторе, заданном для параметра Bearing speed [s1, … sS]. Каждая строка содержит четыре элемента:

_xxs - Демпфирование в направлении x -оси в s^th скорость
_xys - Демпфирование в направлении x -оси, связанное с движением в направлении y -оси в s^th скорость
_yxs - Демпфирование в направлении y -оси, связанное с движением в направлении x -оси в s^th скорость
_yys - Демпфирование в направлении y -оси в s^th скорость

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support:
- Number of supports установлено на 3 или 4.
- Intermediate (I1) mounting type установлено на Speed-dependent bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Intermediate (I1) rotational stiffness [xx,yy]` - Поддержка I1 вращательная жесткость
`[1e4, 1e4]` `N*m/rad` (по умолчанию) | неотрицательный вектор

Вращательная жесткость для поддержки I1. Элементами двухэлементного вектора являются:

xx - Жесткость вокруг оси x -отверстие
yy - Жесткость вокруг оси y -отверстие

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support:
- Number of supports установлено на 3 или 4.
- Intermediate (I1) mounting type установлено на Bearing matrix или Speed-dependent bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Intermediate (I1) translational stiffness [xx,xy,yx,yy]` - Поддержка I1 поступательная жесткость
`[1e6, -2e5, -3e5, 5e]` `N/m` (по умолчанию) | вектор

Поступательная жесткость для поддержки I1. Элементами вектора с четырьмя элементами являются:

xx - Жесткость в x -осевом направлении
xy - Жесткость в направлении x -оси, связанная с движением в направлении y -оси
yx - Жесткость в направлении y -оси, связанная с движением в направлении x -оси
yy - Жесткость в y -осевом направлении

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support:
- Number of supports установлено на 3 или 4.
- Intermediate (I1) mounting type установлено на Bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Intermediate (I1) speed-dependent translational stiffness [xx1,xy1,yx1,yy1;...xxS,xyS,yxS,yyS]` - Поддержка I1 зависимости от скорости поступательной жесткости
`[1e6, -6e5, -3.5e6, 8e6; 1e6, -2e5, -3.0e6, 5e6; 1e6, -5e4, -2.5e6, 3e6]` `N/m` (по умолчанию) | матрица

Зависимая от скорости поступательная жесткость для поддержки I1. Количество строк в матрице должно равняться количеству элементов в векторе, заданном для параметра Bearing speed [s1, … sS]. Каждая строка содержит четыре элемента:

_xxs - Жесткость в направлении x -оси в s^th скорость
_xys - Жесткость в направлении x -оси, связанная с движением в направлении y -оси в s^th скорость
_yxs - Жесткость в направлении y -оси, связанная с движением в направлении x -оси в s^th скорость
_yys - Жесткость в направлении y -оси в s^th скорость

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support:
- Number of supports установлено на 3 или 4.
- Intermediate (I1) mounting type установлено на Speed-dependent bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Intermediate (I2) mounting type` - Поддержка I2 монтажа
`Clamped` (по умолчанию) | `Pinned` | `Free` | `Bearing matrix` | `Speed-dependent bearing matrix`

Тип монтажа на I2 поддержки. I2 поддержки расположен между I1 и F1 поддержек.

Зависимости

Этот параметр видим, когда оба из этих условий выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Supports Number of supports установлено на 4.

`Intermediate (I2) rotational damping [xx,yy]` - Поддержка I2 вращательного демпфирования
`[1e3, 1e3]` `N*m/(rad/s)` (по умолчанию) | вектор

Вращательное демпфирование для поддержки I2. Элементами двухэлементного вектора являются:

xx - Демпфирование вокруг оси x -отверстие
yy - Демпфирование вокруг оси y -отверстие

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support:
- Number of supports установлено на 4.
- Intermediate (I2) mounting type установлено на Pinned, Free, Bearing matrix, или Speed-dependent bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Intermediate (I2) translational damping [xx,xy,yx,yy]` - Поддержка I2 поступательное демпфирование
`[2e4, -4.4e4, -4.4e4, 3.5e5]` `N/(m/s)` (по умолчанию) | вектор

Поступательное демпфирование для поддержки I2. Элементами вектора с четырьмя элементами являются:

xx - Демпфирование в направлении x -оси
xy - Демпфирование в направлении x -оси, связанное с движением в направлении y -оси
yx - Демпфирование в направлении y -оси, связанное с движением в направлении x -оси
yy - Демпфирование в направлении y -оси

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support:
- Number of supports установлено на 4.
- Intermediate (I2) mounting type установлено на Bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Intermediate (I2) speed-dependent translational damping [xx1,xy1,yx1,yy1;...xxS,xyS,yxS,yyS]` - Поддержка I2 зависимости от скорости поступательного демпфирования
`[2e4, -4.4e4, -4.4e4, 3.5e5; 1e4, -2.5e4, -2.5e4, 1.4e5; 5e3, -1.0e4, -1.0e4, 2.0e4]` `N/(m/s)` (по умолчанию) | матрица

Зависящее от скорости поступательное демпфирование для поддержки I2. Количество строк в матрице должно равняться количеству элементов в векторе, заданном для параметра Bearing speed [s1, … sS]. Каждая строка содержит четыре элемента:

_xxs - Демпфирование в направлении x -оси в s^th скорость
_xys - Демпфирование в направлении x -оси, связанное с движением в направлении y -оси в s^th скорость
_yxs - Демпфирование в направлении y -оси, связанное с движением в направлении x -оси в s^th скорость
_yys - Демпфирование в направлении y -оси в s^th скорость

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support:
- Number of supports установлено на 4.
- Intermediate (I2) mounting type установлено на Speed-dependent bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Intermediate (I2) rotational stiffness [xx,yy]` - Поддержка I2 вращательная жесткость
`[1e4, 1e4]` `N*m/rad` (по умолчанию) | неотрицательный вектор

Вращательная жесткость для поддержки I2. Элементами двухэлементного вектора являются:

xx - Жесткость вокруг оси x -отверстие
yy - Жесткость вокруг оси y -отверстие

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support:
- Number of supports установлено на 4.
- Intermediate (I2) mounting type установлено на Bearing matrix или Speed-dependent bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Intermediate (I2) translational stiffness [xx,xy,yx,yy]` - Поддержка I2 поступательная жесткость
`[1e6, -2e5, -3e5, 5e]` `N/m` (по умолчанию) | вектор

Поступательная жесткость для поддержки I2. Элементами вектора с четырьмя элементами являются:

xx - Жесткость в x -осевом направлении
xy - Жесткость в направлении x -оси, связанная с движением в направлении y -оси
yx - Жесткость в направлении y -оси, связанная с движением в направлении x -оси
yy - Жесткость в y -осевом направлении

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support:
- Number of supports установлено на 4.
- Intermediate (I2) mounting type установлено на Bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Intermediate (I2) speed-dependent translational stiffness [xx1,xy1,yx1,yy1;...xxS,xyS,yxS,yyS]` - Поддержка I2 зависимости от скорости поступательной жесткости
`[1e6, -6e5, -3.5e6, 8e6; 1e6, -2e5, -3.0e6, 5e6; 1e6, -5e4, -2.5e6, 3e6]` `N/m` (по умолчанию) | вектор

Зависимая от скорости поступательная жесткость для поддержки I2. Количество строк в матрице должно равняться количеству элементов в векторе, заданном для параметра Bearing speed [s1, … sS]. Каждая строка содержит четыре элемента:

_xxs - Жесткость в направлении x -оси в s^th скорость
_xys - Жесткость в направлении x -оси, связанная с движением в направлении y -оси в s^th скорость
_yxs - Жесткость в направлении y -оси, связанная с движением в направлении x -оси в s^th скорость
_yys - Жесткость в направлении y -оси в s^th скорость

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support:
- Number of supports установлено на 4.
- Intermediate (I2) mounting type установлено на Speed-dependent bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Follower (F1) mounting type` - Поддержка F1 монтажа
`Clamped` (по умолчанию) | `Pinned` | `Free` | `Bearing matrix` | `Speed-dependent bearing matrix`

Тип монтажа на последующем конце вала.

Зависимости

Установка этого параметра на Pinned, Free, Bearing matrix, или Speed-dependent bearing matrix отображает связанные параметры. Для получения дополнительной информации смотрите Зависимости параметров типа монтажа и Зависимости параметров типа монтажа.

`Follower (F1) rotational damping [xx,yy]` - Поддержка F1 вращательного демпфирования
`[1e3, 1e3]` `N*m/(rad/s)` (по умолчанию) | вектор

Вращательное демпфирование для F1 поддержки, которое является поддержкой, расположенной ближе всего к F, последующему концу вала. Элементами двухэлементного вектора являются:

xx - Демпфирование вокруг оси x -отверстие
yy - Демпфирование вокруг оси y -отверстие

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support Follower (F1) mounting type установлено на Pinned, Free, Bearing matrix, или Speed-dependent bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Follower (F1) translational damping [xx,xy,yx,yy]` - Поддержка F1 поступательное демпфирование
`[2e4, -4.4e4, -4.4e4, 3.5e5]` `N/(m/s)` (по умолчанию) | вектор

Поступательное демпфирование для F1 поддержки, которое является поддержкой, ближайшим к F, последующим концом вала. Элементами вектора с четырьмя элементами являются:

xx - Демпфирование в направлении x -оси
xy - Демпфирование в направлении x -оси, связанное с движением в направлении y -оси
yx - Демпфирование в направлении y -оси, связанное с движением в направлении x -оси
yy - Демпфирование в направлении y -оси

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support Follower (F1) mounting type установлено на Bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Follower (F1) speed-dependent translational damping [xx1,xy1,yx1,yy1;...xxS,xyS,yxS,yyS]` - Поддержка F1 зависимости от скорости поступательного демпфирования
`[2e4, -4.4e4, -4.4e4, 3.5e5; 1e4, -2.5e4, -2.5e4, 1.4e5; 5e3, -1.0e4, -1.0e4, 2.0e4]` `N/(m/s)` (по умолчанию) | матрица

Зависящее от скорости поступательное демпфирование для F1 поддержки, которое является поддержкой, ближайшим к F, последующим концом вала.

Количество строк в матрице должно равняться количеству элементов в векторе, заданном для параметра Bearing speed [s1, … sS]. Каждая строка содержит четыре элемента:

_xxs - Демпфирование в направлении x -оси в s^th скорость
_xys - Демпфирование в направлении x -оси, связанное с движением в направлении y -оси в s^th скорость
_yxs - Демпфирование в направлении y -оси, связанное с движением в направлении x -оси в s^th скорость
_yys - Демпфирование в направлении y -оси в s^th скорость

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support Follower (F1) mounting type установлено на Speed-dependent bearing matrix. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Follower (F1) rotational stiffness [xx,yy]` - Поддержка F1 вращательная жесткость
`[1e4, 1e4]` `N*m/rad` (по умолчанию) | неотрицательный вектор

Вращательная жесткость для F1 поддержки, которая является поддержкой, которая наиболее близка к F, последующему концу вала. Элементами двухэлементного вектора являются:

xx - Жесткость вокруг оси x -отверстие
yy - Жесткость вокруг оси y -отверстие

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support Follower (F1) mounting type установлено на Bearing matrix или Speed-dependent bearing matrix. Для получения дополнительной информации смотрите Зависимости параметров типа монтажа и Зависимости параметров типа монтажа.

`Follower (F1) translational stiffness [xx,xy,yx,yy]` - Поддержка F1 поступательная жесткость
`[1e6, -2e5, -3e5, 5e]` `N/m` (по умолчанию) | вектор

Поступательная жесткость для F1 поддержки, которая является поддержкой, которая наиболее близка к F, последующему концу вала. Элементами вектора с четырьмя элементами являются:

xx - Жесткость в x -осевом направлении
xy - Жесткость в направлении x -оси, связанная с движением в направлении y -оси
yx - Жесткость в направлении y -оси, связанная с движением в направлении x -оси
yy - Жесткость в y -осевом направлении

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support Follower (F1) mounting type установлено на Bearing matrix. Для получения дополнительной информации смотрите Зависимости параметров типа монтажа и Зависимости параметров типа монтажа.

`Follower (F1) speed-dependent translational stiffness [xx1,xy1,yx1,yy1;...xxS,xyS,yxS,yyS]` - Поддержка F1 зависимости от скорости поступательной жесткости
`[1e6, -6e5, -3.5e6, 8e6; 1e6, -2e5, -3.0e6, 5e6; 1e6, -5e4, -2.5e6, 3e6]` `N/m` (по умолчанию) | матрица

Зависимая от скорости поступательная жесткость для F1 поддержки, которая является поддержкой, которая наиболее близка к F, последующему концу вала.

_xxs - Жесткость в направлении x -оси в s^th скорость
_xys - Жесткость в направлении x -оси, связанная с движением в направлении y -оси в s^th скорость
_yxs - Жесткость в направлении y -оси, связанная с движением в направлении x -оси в s^th скорость
_yys - Жесткость в направлении y -оси в s^th скорость

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support Follower (F1) mounting type установлено на Speed-dependent bearing matrix. Для получения дополнительной информации смотрите Зависимости параметров типа монтажа и Зависимости параметров типа монтажа.

`Bearing speed [s1,...,sS]` - Поддержка вращения опорного подшипника
`[200, 500, 1500]` `rpm` (по умолчанию) | неотрицательный вектор

Поддерживайте скорость вращения подшипника.

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft Model bending установлено на On. Для получения дополнительной информации см. «Зависимости параметра вала».
В настройках Support, по крайней мере, один из этих параметров установлен в Speed-dependent bearing matrix:
- Base (B1) mounting type
- Intermediate (I1) mounting type
- Intermediate (I2) mounting type
- Follower (F1) mounting type

Для получения дополнительной информации смотрите Зависимости параметров типа монтажа и Зависимости параметров типа монтажа.

Изгиб

Настройки Bending видны, когда в настройках Shaft параметр Model bending установлен на On. Для получения дополнительной информации смотрите Модель изгиба.

Таблица показывает, как в настройках Bending заданное значение для параметра Rigid masses concentrically attached to shaft влияет на видимость связанных параметров. Чтобы узнать, как считать таблицу, см. «Параметры».

Зависимости параметров твердых масс, концентрически присоединенных к валу

Rigid Masses Concentrically Attached to Shaft
`None`	`Point mass`	`Disk`
-	Rigid mass distances from base (B)	Rigid mass distances from base (B)
	Rigid masses	Rigid masses
		Rigid mass diametric moments of inertia about axis perpendicular to shaft
		Rigid mass polar moments of inertia about shaft axis

`Damping constant proportional to mass` - Демпфирование постоянной α
`10` `1/s` (по умолчанию) | положительная скалярная величина

Демпфирующая константа, α, пропорциональная массе.

Когда модель изгиба собственных моделей включена, демпфер перемещения в каждой модальной системе масса-пружина-демпфер имеет коэффициент демпфирования _aMMode, где _MMode является модальной массой.

Когда включена модель сгибания кусковой массы, в систему добавляется демпфирующая матрица, αM. M - уравнение большой матрицы движения.

Зависимости

Этот параметр видим, когда в настройках Shaft параметр Model bending равен On. Для получения дополнительной информации смотрите Модель изгиба.

`Damping constant proportional to stiffness` - Константа демпфирования β
`1e-8` `s` (по умолчанию) | положительная скалярная величина

Демпфирующая константа, β, пропорциональная жесткости.

Когда включена модель сгибания кусковой массы, в систему добавляется демпфирующая матрица, βK. K - уравнение матрицы жесткости движения. Когда модель изгиба собственных моделей включена, в систему добавляется _βKModal демпфирования.

Зависимости

`Rigid masses concentrically attached to shaft` - Тип жестких масс, прикрепленных к валу
`None` (по умолчанию) | `Point mass` | `Disk`

Введите, если таковые имеются, твердые массы, прикрепленные к валу.

Зависимости

Заданное значение для этого параметра влияет на видимость связанных параметров. Для получения дополнительной информации см. Раздел «Жесткие массы, концентрически присоединенные к параметрам вала».

`Rigid mass distances from base (B)` - Расположение твердых масс вдоль вала на расстоянии от базового узла
`0.5` `m` (по умолчанию) | неотрицательный скаляр или вектор

Расположение жесткой массы вдоль вала на расстоянии от B, базового конца вала. Для нескольких масс задайте увеличение вектора-строки. Количество элементов в векторе должно быть равно количеству масс, присоединенных к валу. Значение скаляра или, для нескольких масс, наибольшее значение в векторе не должно превышать длину вала.

Зависимости

Этот параметр видим, когда оба из этих условий выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Bending параметр Rigid masses concentrically attached to shaft устанавливается на Point mass или Disk. Для получения дополнительной информации см. Раздел «Жесткие массы, концентрически присоединенные к параметрам вала».

`Rigid masses` - Масса жестких масс, концентрически присоединенных к валу
`2` `kg` (по умолчанию) | положительная скалярная величина или вектор

Масса жестких масс, концентрически присоединенных к валу. Для нескольких масс задайте вектор-строку. Количество и порядок элементов в векторе должны соответствовать элементам в векторе, заданным для параметра Rigid mass distances from base (B).

Зависимости

Этот параметр видим, когда оба из этих условий выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Bending параметр Rigid masses concentrically attached to shaft устанавливается на Point mass или Disk. Для получения дополнительной информации см. Раздел «Жесткие массы, концентрически присоединенные к параметрам вала».

`Rigid mass diametric moments of inertia about axis perpendicular to shaft` - Диаметральные моменты инерции вокруг оси, перпендикулярной валу
`0.025` `kg*m^2` (по умолчанию) | положительная скалярная величина или вектор

Моменты инерции твердой массы вокруг оси, перпендикулярной валу. Для нескольких масс задайте вектор-строку. Количество и порядок элементов в векторе должны соответствовать элементам в векторе, заданным для параметра Rigid mass distances from base (B).

Зависимости

Этот параметр видим, когда оба из этих условий выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Bending параметр Rigid masses concentrically attached to shaft устанавливается на Disk. Для получения дополнительной информации см. Раздел «Жесткие массы, концентрически присоединенные к параметрам вала».

`Rigid mass polar moments of inertia about shaft axis` - Полярные моменты инерции вокруг оси вала
`0.050` `kg*m^2` (по умолчанию) | положительная скалярная величина или вектор

Жесткие моменты инерции полярной массы вокруг оси вала. Для нескольких масс задайте вектор-строку. Количество и порядок элементов в векторе должны соответствовать элементам в векторе, заданным для параметра Rigid mass distances from base (B).

Зависимости

Этот параметр видим, когда оба из этих условий выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Bending параметр Rigid masses concentrically attached to shaft устанавливается на Disk. Для получения дополнительной информации см. Раздел «Жесткие массы, концентрически присоединенные к параметрам вала».

`Static unbalances that excite bending` - Возбуждение статических дисбалансов
`[.01, .01]` `m*kg` (по умолчанию) | неотрицательный вектор

Статические дисбалансы, которые возбуждают изгиб.

Зависимости

`Static unbalance distances from base (B)` - Статические расстояния дисбаланса от основы
`[.33, .67]` `m` (по умолчанию) | неотрицательный вектор

Расстояние возбуждающих статических дисбалансов от B, базового конца вала.

Зависимости

`Static unbalance offset angles` - Статические углы смещения дисбаланса
`[0, pi]` `rad` (по умолчанию) | неотрицательный вектор

Начальный угол, вокруг осевой линии вала относительно оси x, возбуждающих статических дисбалансов.

Зависимости

Усовершенствованный изгиб

Настройки Advanced Bending доступны, когда в настройках Shaft параметр Model bending установлен на On. Для получения дополнительной информации смотрите Модель изгиба.

В настройках Advanced Bending значение параметра Bending vibration analysis method влияет на видимость параметров в настройках Supports. Для получения дополнительной информации смотрите Метод анализа изгибных вибраций.

Таблица Advanced Bending Parameter Dependencies показывает, как видимость определенных параметров в настройках Advanced Bending зависит от значений для комбинации параметров в одной или нескольких из следующих настроек:

Shaft
Supports
Advanced Bending

Например, параметр Simulated eigenmode dependency on rotation speed видим, если все эти условия удовлетворены:

В настройках Shaft Model bending установлено на On.
В настройках Supports, по крайней мере, один параметр Mounting type установлен в Speed-dependent bearing matrix.
В настройках Advanced Bending Bending vibration analysis method установлено на Eigenmodes.

Advanced Bending параметров

Установка > Параметр	Заданные значения параметров и зависимые параметры Advanced Bending
Shaft> Model bending	`Off`	`On`
Supports> Mounting type	-	Любая комбинация `Clamped`, `Pinned`, `Free`, или `Bearing matrix`			По крайней мере, один `Speed-dependent bearing matrix` и любая комбинация `Clamped`, `Pinned`, `Free`, или `Bearing matrix`
В столбцах справа показаны параметры Advanced Bending, которые видны для конфигурации модели параметра, показанного в соответствующем столбце в строках заголовка этой таблицы.	-	Bending vibration analysis method			Bending vibration analysis method
		`Lumped mass`	`Eigenmodes`		`Lumped mass`	`Eigenmodes`
			Bending mode determination			Bending mode determination
			`Simscape determined`	`User Defined`		`Simscape determined`		`User Defined`
			Limit number of modes			Limit number of modes		`User Defined`
						Simulated eigenmode dependency on rotation speed		Simulated eigenmode dependency on rotation speed
						`Static`	`Dynamic`	`Static`	`Dynamic`
						Nominal shaft speed for bending modes	`Dynamic`	Nominal shaft speed for bending modes
			Eigenfrequency upper limit			Eigenfrequency upper limit	Eigenfrequency upper limit
			Shaft length increments for mode shape computations			Shaft length increments for mode shape computations	Shaft length increments for mode shape computations
				Modal frequencies [m]				Modal frequencies [s, m]	Modal frequencies [s, m]
				Shaft position [z]				Shaft position [z]	Shaft position [z]
				X-direction mode shapes [z,m]				X-direction mode shapes [z,m,s]	X-direction mode shapes [z,m,s]
				Y-direction mode shapes [z,m]				Y-direction mode shapes [z,m,s]	Y-direction mode shapes [z,m,s]

`Bending vibration analysis method` - Метод анализа изгибных вибраций
`Lumped mass` (по умолчанию) | `Eigenmodes`

СПОСОБ АНАЛИЗА ВИБРАЦИИ ИЗГИБА. Для получения дополнительной информации смотрите Метод изгиба Модели кусковой массы и Метод изгиба Модели собственных модах.

Зависимости

Значение этого параметра влияет на видимость других параметров в настройках Advanced Bending. Для получения дополнительной информации смотрите Дополнительные зависимости параметра изгиба.

`Bending mode determination` - Метод определения режима изгиба
`Simscape determined` (по умолчанию) | `User defined`

Метод определения собственных частот и форм модели:

Simscape determined - Simscape определяет режим на основе заданных граничных условий.
User defined - Задайте частоты и формы собственной модели непосредственно.

Зависимости

Этот параметр видим, когда оба из этих условий выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Advanced Bending параметр Bending vibration analysis method устанавливается на Eigenmodes. Для получения дополнительной информации смотрите Дополнительные зависимости параметра изгиба.

Значение этого параметра влияет на видимость других параметров в настройках Advanced Bending. Для получения дополнительной информации см. Раздел «Зависимости параметров типа монтажа».

`Limit number of modes` - Максимальное количество режимов
`6` (по умолчанию) | положительный целочисленный скаляр

Максимальное количество режимов, которые Simscape определяет.

Зависимости

Этот параметр видим, когда оба из этих условий выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Advanced Bending параметр Bending vibration analysis method устанавливается на Eigenmodes и параметру Bending mode determination задано значение Simscape determined. Для получения дополнительной информации смотрите Дополнительные зависимости параметра изгиба.

`Simulated eigenmode dependency on rotation speed` - Зависимость Eigenmode
`Static` (по умолчанию) | `Dynamic`

Моделируемая зависимость свойств собственной модели от скорости вращения вала:

Статический - анализ изгиба удерживает свойства собственной модели постоянными во время изменения скорости вращения вала.
Динамический - анализ изгиба регулирует свойства собственной модели, когда изменяется скорость вращения вала. Блок использует элементы вектора, заданные для параметра Bearing speed [s1,…, sS], в качестве ссылочных точек интерполяционной таблицы. Для этой модели относительные величины зависящих от скорости элементов поступательной жесткости могут не изменяться при каждой скорости подшипника.

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Supports, по крайней мере, один параметр типа монтажа установлен в Speed-dependent bearing matrix.
В настройках Advanced Bending параметр Bending vibration analysis method устанавливается на Eigenmodes. Для получения дополнительной информации смотрите Дополнительные зависимости параметра изгиба.

`Nominal shaft speed for bending modes` - Номинальная скорость вала
`5000` `rpm` (по умолчанию) | скаляром

Номинальная скорость вала для анализа режима изгиба.

Зависимости

Этот параметр видим, если все эти условия выполнены:

В настройках Shaft параметр Model bending устанавливается на On.
В настройках Supports, по крайней мере, один параметр типа монтажа установлен в Speed-dependent bearing matrix.
В настройках Advanced Bending:
- Параметр Bending vibration analysis method установлен в Eigenmodes.
- Параметр Simulated eigenmode dependency on rotation speed установлен в Static.

Для получения дополнительной информации смотрите Дополнительные зависимости параметра изгиба.

`Eigenfrequency upper limit` - верхний предел собственной частоты
`1e8` `rpm` (по умолчанию) | положительный целочисленный скаляр

Верхний предел собственной частоты.

Зависимости

Этот параметр видим, когда оба из этих условий выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Advanced Bending параметр Bending vibration analysis method устанавливается на Eigenmodes и параметру Bending mode determination задано значение Simscape determined. Для получения дополнительной информации смотрите Дополнительные зависимости параметра изгиба.

`Shaft length increments for mode shape computations` - шаги длины вала
`0.01` `m` (по умолчанию) | положительная скалярная величина

Шаги длины вала, используемый для расчетов массы и формы режима. Для получения дополнительной информации см. «Метод изгиба модели собственных моделей».

Зависимости

Этот параметр видим, когда оба из этих условий выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Advanced Bending параметр Bending vibration analysis method устанавливается на Eigenmodes и параметру Bending mode determination задано значение Simscape determined. Для получения дополнительной информации смотрите Дополнительные зависимости параметра изгиба.

`Modal frequencies [m]` - Несущие-независимые от скорости модальные частоты
`[280, 644, 615, 1285]` `rad/s` (по умолчанию) | неотрицательный вектор

Модальные частоты для модели, не зависящей от скорости подшипника. Для получения дополнительной информации см. «Метод изгиба модели собственных моделей».

Зависимости

Этот параметр видим, когда оба из этих условий выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Supports никакие типы монтажа не устанавливаются в Speed-dependent bearing matrix.
В настройках Advanced Bending:
- Bending vibration analysis method установлено на Eigenmodes.
- Bending mode determination установлено на User defined.

Для получения дополнительной информации смотрите Дополнительные зависимости параметра изгиба.

`Modal frequencies [s,m]` - Зависящие от скорости подшипника модальные частоты
`[257, 780, 580, 1560; 280, 644, 615, 1285; 294, 513, 636, 1020]` `rad/s` (по умолчанию) | неотрицательную матрицу

Модальные частоты для модели, зависящей от скорости подшипника. Для получения дополнительной информации см. «Метод изгиба модели собственных моделей».

Зависимости

Этот параметр видим, когда оба из этих условий выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Supports, по крайней мере, один тип монтажа установлен в Speed-dependent bearing matrix .
В настройках Advanced Bending:
- Bending vibration analysis method установлено на Eigenmodes.
- Bending mode determination установлено на User defined.

Для получения дополнительной информации смотрите Дополнительные зависимости параметра изгиба.

`Shaft position [z]` - Положение вала
`[0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1]` (по умолчанию) | увеличение неотрицательного вектора

Положение вала для форм режима. Количество элементов в векторе соответствует количеству строк в X формах режима -pirection и Y-pirection. Для получения дополнительной информации см. «Метод изгиба модели собственных моделей».

Зависимости

Этот параметр видим, когда оба из этих условий выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Advanced Bending:
- Bending vibration analysis method установлено на Eigenmodes.
- Bending mode determination установлено на User defined.

Для получения дополнительной информации смотрите Дополнительные зависимости параметра изгиба.

`X-direction mode shapes [z,m]` - Формы независимо от скорости подшипника X -направления
`[.1648, .0086, -.2759, .0162; .1671, .0093, -.2231, .0133; .1691, .01, -.1689, .0102; .1707, .0105, -.1135, .007; .1717, .0108, -.057, .0035; .1721, .0109, 0, 0; .1717, .0108, .057, -.0035; .1707, .0105, .1135, -.007; .1691, .01, .1689, -.0102; .1671, .0093, .2231, -.0133; .1648, .0086, .2759, -.0162]` (по умолчанию) | матрица

X - способ направления формирует матрицу для скорости подшипника независимая модель. Для получения дополнительной информации см. «Метод изгиба модели собственных моделей».

Матрица должна иметь размерности z -by- m, где:

z - количество элементов в заданном векторе для параметра Shaft position [z].
m - количество столбцов в указанном векторе для параметра Modal frequencies.

Матрица формы режима имеет вид [_U1x, _U2x,..., _Umx], где каждый столбец является отклонением формы режима в X направлении для m^th режим. Алгоритм вычисляет модальные свойства на основе параметров в настройках Shaft и Bending.

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Supports тип монтажа не устанавливается на Speed-dependent bearing matrix .
В настройках Advanced Bending:
- Bending vibration analysis method установлено на Eigenmodes.
- Bending mode determination установлено на User defined.

Для получения дополнительной информации смотрите Дополнительные зависимости параметра изгиба.

`X-direction mode shapes [z,m,s]` - Формы X -направления, зависящие от скорости подшипника
cat(3, [.1842, .0134, -.3072, .0272; .1863, .0152, -.2482, .0226; .1882, .0169, -.1878, .0176; .1897, .0182, -.1261, .0121; .1906, .019, -.0634, .0062; .191, .0193, 0, 0; .1906, .019, .0634, -.0062; .1897, .0182, .1261, -.0121; .1882, .0169, .1878, -.0176; .1863, .0152, .2482, -.0226; .1842, .0134, .3072, -.0272], [.1648, .0086, -.2759, .0162; .1671, .0093, -.2231, .0133; .1691, .01, -.1689, .0102; .1707, .0105, -.1135, .007; .1717, .0108, -.057, .0035; .1721, .0109, 0, 0; .1717, .0108, .057, -.0035; .1707, .0105, .1135, -.007; .1691, .01, .1689, -.0102; .1671, .0093, .2231, -.0133; .1648, .0086, .2759, -.0162], [.1291, .0046, -.2166, .0082; .131, .0048, -.1751, .0067; .1327, .005, -.1327, .0051; .1341, .0052, -.0891, .0035; .135, .0053, -.0448, .0017; .1353, .0053, 0, 0; .135, .0053, .0448, -.0017; .1341, .0052, .0891, -.0035; .1327, .005, .1327, -.0051; .131, .0048, .1751, -.0067; .1291, .0046, .2166, -.0082]) (по умолчанию) | матрица

X - способ направления формирует матрицу для зависимой от скорости от подшипника модели. Для получения дополнительной информации см. «Метод изгиба модели собственных моделей».

Матрица должна иметь размерности z -by- m -by- s, где:

z - количество элементов в заданном векторе для параметра Shaft position [z].
m - количество коплумнов в заданном векторе для параметра Modal frequencies [z,m].
s - количество элементов в заданном векторе для параметра Bearing speed [s1,…, sS].

Матрица формы режима имеет вид cat (3, _[U1x1, _U2x1,..._{, Umx1}],..., _[U1xs_{, U2xs},.._., Umxs]), где каждый столбец является отклонением формы режима в x направлении для m^th режим. Каждая страница соответствует элементу в векторе, заданному для параметра Bearing speed [s1,…, sS]. Алгоритм вычисляет модальные свойства на основе параметров в настройках Shaft и Bending.

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Supports, по крайней мере, один тип монтажа установлен в Speed-dependent bearing matrix .
В настройках Advanced Bending:
- Bending vibration analysis method установлено на Eigenmodes.
- Bending mode determination установлено на User defined.

Для получения дополнительной информации смотрите Дополнительные зависимости параметра изгиба.

`Y-direction mode shapes [z,m]` - Формы независимо от скорости подшипника Y -направления
`[.1193, -.1784, -.1997, -.3348; .1209, -.1933, -.1615, -.2751; .1224, -.2068, -.1223, -.2119; .1235, -.2176, -.0821, -.1445; .1243, -.2245, -.0413, -.0734; .1246, -.2269, 0, 0; .1243, -.2245, .0413, .0734; .1235, -.2176, .0821, .1445; .1224, -.2068, .1223, .2119; .1209, -.1933, .1615, .2751; .1193, -.1784, .1997, .3348]` (по умолчанию) | матрица

Y - способ направления формирует матрицу для скорости подшипника независимая модель. Для получения дополнительной информации см. «Метод изгиба модели собственных моделей».

Матрица должна иметь размерности z -by- m, где:

z - количество элементов в заданном векторе для параметра Shaft position [z].
m - количество столбцов в указанном векторе для параметра Modal frequencies.

Матрица формы режима имеет вид [_U1y, _U2y,..., _Umy], где каждый столбец является отклонением формы режима в Y направлении, для m^th режим. Алгоритм вычисляет модальные свойства на основе параметров в настройках Shaft и Bending.

Зависимости

Этот параметр видим, когда оба из этих условий выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Supports тип монтажа не устанавливается на Speed-dependent bearing matrix .
В настройках Advanced Bending:
- Bending vibration analysis method установлено на Eigenmodes.
- Bending mode determination установлено на User defined.

Для получения дополнительной информации смотрите Дополнительные зависимости параметра изгиба.

`Y-direction mode shapes [z,m,s]` - Формы y -направления, зависящие от скорости подшипника
cat(3, [.0885, -.1625, -.1475, -.3301; .0895, -.1847, -.1192, -.2745; .0904, -.2048, -.0902, -.2141; .0911, -.2209, -.0606, -.1475; .0916, -.2313, -.0304, -.0754; .0917, -.2349, 0, 0; .0916, -.2313, .0304, .0754; .0911, -.2209, .0606, .1475; .0904, -.2048, .0902, .2141; .0895, -.1847, .1192, .2745; .0885, -.1625, .1475, .3301], [.1193, -.1784, -.1997, -.3348; .1209, -.1933, -.1615, -.2751; .1224, -.2068, -.1223, -.2119; .1235, -.2176, -.0821, -.1445; .1243, -.2245, -.0413, -.0734; .1246, -.2269, 0, 0; .1243, -.2245, .0413, .0734; .1235, -.2176, .0821, .1445; .1224, -.2068, .1223, .2119; .1209, -.1933, .1615, .2751; .1193, -.1784, .1997, .3348], [.1566, -.1901, -.2628, -.3377; .1589, -.1994, -.2125, -.2753; .161, -.2079, -.1609, -.2103; .1627, -.2146, -.1081, -.1424; .1638, -.219, -.0544, -.0719; .1642, -.2205, 0, 0; .1638, -.219, .0544, .0719; .1627, -.2146, .1081, .1424; .161, -.2079, .1609, .2103; .1589, -.1994, .2125, .2753; .1566, -.1901, .2628, .3377]) (по умолчанию) | матрица

Y - способ направления формирует матрицу для зависимой от скорости от подшипника модели. Для получения дополнительной информации см. «Метод изгиба модели собственных моделей».

Матрица должна иметь размерности z -by- m -by- s, где:

z - количество элементов в заданном векторе для параметра Shaft position [z].
m - количество столбцов в указанном векторе для параметра Modal frequencies [z,m].
s - количество элементов в заданном векторе для параметра Bearing speed [s1,…, sS].

Матрица формы режима имеет вид cat (3, _[U1y1, _U2y1,..._{, Umy1}],..., _[U1ys_{, U2ys},.._., Umys]), где каждый столбец является отклонением формы режима в y направлении для m^th режим. Каждая страница соответствует элементу в векторе, заданному для параметра Bearing speed [s1,…, sS]. Алгоритм вычисляет модальные свойства на основе параметров в настройках Shaft и Bending.

Зависимости

Этот параметр видим, когда все эти условия выполняются:

В настройках Shaft параметр Model bending устанавливается на On. Для получения дополнительной информации смотрите Модель изгиба.
В настройках Supports, по крайней мере, один тип монтажа установлен в Speed-dependent bearing matrix .
В настройках Advanced Bending:
- Bending vibration analysis method установлено на Eigenmodes.
- Bending mode determination установлено на User defined.

Для получения дополнительной информации смотрите Дополнительные зависимости параметра изгиба.

Примеры моделей

Гибкий Вал

Два гибких алюминиевых вала, смоделированных с помощью подхода комкнутого параметра. Оба вала состоят из 20 сегментов, содержащих инерцию, демпфирование и жесткие скручивающие пружины. В начале симуляции муфта разблокируется и ведомый вал свободен. Обратите внимание, что начальная скорость вала мотора установлена равной 200 рад/с и что система начинается в установившемся состоянии. Муфта входит в зацепление и разъединяется во время испытания, и во время каждого события эффект гибкости вала может быть замечен в результатах симуляции.

Shaft with Torsional and Transverse Flexibility

Вал с кручением и поперечной гибкостью

Два гибких вала, которые имеют кручение и поперечную гибкость. Один вал вычисляет поперечное движение с помощью вычисленных собственных мод, а другой вал использует подход с комчатым параметром. Граничные условия на валах могут быть изменены на масках блоков.

Ссылки

[1] Adams, M.L. Вращающаяся Вибрация Машины. CRC Press, NY: 2010.

[2] Bathe, K. J. Finite Element Procedures. Prentice Hall, 1996.

[3] Чудновский, В., Д. Кеннеди, А. Мукерджи и Дж. Вендландт. Моделирование гибких тел в SimMechanics и Simulink. MATLAB Digest, Том 14, Номер 3. Май 2006.

[4] Miller, S., T. Soares, Y. Van Weddingen, J. Wendlandt. Моделирование гибких тел с Simscape Multibody. The MathWorks, 2017.

[5] Мушинска, А. Ротординамика. Тейлор и Фрэнсис, 2005

[6] Рао, С.С. Вибрация непрерывных систем. Hoboken, NJ: John Wiley & Sons, 2007.

См. также

Темы

Решите проблемы симуляции решателя секционирования для моделей Simscape Driveline

Введенный в R2018b

Документация

Flexible Shaft

Описание

Модель кручения

Модели изгиба

Улучшите скорость симуляции или точность

Допущения и ограничения

Порты

Выход

Fr - Усилие на опоры подшипника физический сигнал

Зависимости

M - Момент на опорах подшипника физический сигнал

Зависимости

V - Поступательная скорость вала физический сигнал

Зависимости

W - Угловая скорость вала физический сигнал

Зависимости

Сохранение

B - Основа вращательный механический

F - Последующий вращательный механический

Параметры

Вал

Model bending - опция модели изгиба Off (по умолчанию) | On

Зависимости

Minimum number of flexible elements - Минимальное количество гибких элементов 1 (по умолчанию) | положительное целое число

Parameterization - Метод параметризации By stiffness and inertia (по умолчанию) | By material and geometry | By segment stiffness and inertia | By material and segment geometry

Зависимости

Shaft length - Длина вала 1 m (по умолчанию) | положительная скалярная величина

Зависимости

Segment lengths [B,...,F] - Длина каждого сегмента вала [1, .5, .25] (по умолчанию) | вектор

Зависимости

Torsional stiffness - Жесткость материала 2e5 N*m/rad (по умолчанию) | положительная скалярная величина

Зависимости

Segment torsional stiffness [B,...,F] - Жесткость материала для каждого сегмента вала [400000, 200000, 100000] N*m/rad (по умолчанию) | положительный вектор

Зависимости

Torsional Inertia - Полярный момент инерции 0.02 kg*m^2 (по умолчанию) | положительная скалярная величина

Зависимости

Segment torsional inertia [B,...,F] - Полярный момент инерции для каждого сегмента вала [.025, .02, .015] kg*m^2 (по умолчанию) | положительный вектор

Зависимости

Bending rigidity - Жесткость изгиба 5e5 m^4*Pa (по умолчанию) | положительная скалярная величина

Зависимости

Segment bending rigidity [B,...,F] - Жесткость изгиба каждого сегмента [600000, 500000, 400000] m^4*Pa (по умолчанию) | положительный вектор

Зависимости

Linear density - Плотность на единицу длины 19 kg/m (по умолчанию) | положительная скалярная величина

Зависимости

Segment linear density [B,...,F] - Плотность на единицу длины для каждого сегмента [20, 19, 18] kg/m (по умолчанию) | положительный вектор

Зависимости

Material density - Плотность материала 7.8e3 kg/m^3 (по умолчанию) | положительная скалярная величина

Зависимости

Shear modulus - Модуль сдвига 7.93e9 Pa (по умолчанию) | положительная скалярная величина

Зависимости

Young's modulus - Модуль Юнга 200e9 Pa (по умолчанию) | положительная скалярная величина

Зависимости

Shaft geometry - Геометрия поперечного сечения Solid (по умолчанию) | Annular

Зависимости

Shaft outer diameter - Наружный диаметр вала 0.075 m (по умолчанию) | положительная скалярная величина

Зависимости

Segment outer diameter [B,...,F] - Наружный диаметр для каждого сегмента вала [.085, .075, .065] m (по умолчанию) | положительный вектор

Зависимости

Shaft inner diameter - Внутренний диаметр вала 0.05 m (по умолчанию) | позитвенный скаляр

Зависимости

Segment inner diameter [B,...,F] - Внутренний диаметр для каждого сегмента вала [.055, .05, .045] m (по умолчанию) | вектор

Зависимости

Скрученность

Damping ratio from internal losses - коэффициент затухания материала 0.01 (по умолчанию) | положительная скалярная величина

Viscous friction coefficients at base (B) and follower (F) - Коэффициенты вязкого трения [0, 0] N*m/(rad/s) (по умолчанию) | неотрицательный вектор

Зависимости

Viscous friction coefficients at each support [B1,...,F1] - Коэффициенты вязкого трения [0, 0] N*m/(rad/s) (по умолчанию) | неотрицательный вектор

Зависимости

Initial shaft torsional deflection - Начальное кручение вала 0 rad (по умолчанию) | неотрицательной скаляром

Initial shaft angular velocity - Начальная скорость вращения 0 rpm (по умолчанию) | неотрицательной скаляром

Поддержки

Number of supports - Количество поддержек 2 (по умолчанию) | 3 | 4

Зависимости

Support locations relative to base (B) - Места оказания поддержки [0, 1] m (по умолчанию) | неотрицательный вектор увеличения

Зависимости

Base (B1) mounting type - Поддержка B1 монтажа Clamped (по умолчанию) | Pinned | Free | Bearing matrix | Speed-dependent bearing matrix

Зависимости

Base (B1) rotational damping [xx,yy] - Поддержка B1 вращательного демпфирования [1e3, 1e3] N*m/(rad/s) (по умолчанию) | вектор

Зависимости

`Fr` - Усилие на опоры подшипника
физический сигнал

`M` - Момент на опорах подшипника
физический сигнал

`V` - Поступательная скорость вала
физический сигнал

`W` - Угловая скорость вала
физический сигнал

`B` - Основа
вращательный механический

`F` - Последующий
вращательный механический

`Model bending` - опция модели изгиба
`Off` (по умолчанию) | `On`

`Minimum number of flexible elements` - Минимальное количество гибких элементов
`1` (по умолчанию) | положительное целое число

`Parameterization` - Метод параметризации
`By stiffness and inertia` (по умолчанию) | `By material and geometry` | `By segment stiffness and inertia` | `By material and segment geometry`

`Shaft length` - Длина вала
`1` `m` (по умолчанию) | положительная скалярная величина

`Segment lengths [B,...,F]` - Длина каждого сегмента вала
`[1, .5, .25]` (по умолчанию) | вектор

`Torsional stiffness` - Жесткость материала
`2e5` `N*m/rad` (по умолчанию) | положительная скалярная величина

`Segment torsional stiffness [B,...,F]` - Жесткость материала для каждого сегмента вала
`[400000, 200000, 100000]` `N*m/rad` (по умолчанию) | положительный вектор

`Torsional Inertia` - Полярный момент инерции
`0.02` `kg*m^2` (по умолчанию) | положительная скалярная величина

`Segment torsional inertia [B,...,F]` - Полярный момент инерции для каждого сегмента вала
`[.025, .02, .015]` `kg*m^2` (по умолчанию) | положительный вектор

`Bending rigidity` - Жесткость изгиба
`5e5` `m^4*Pa` (по умолчанию) | положительная скалярная величина

`Segment bending rigidity [B,...,F]` - Жесткость изгиба каждого сегмента
`[600000, 500000, 400000]` `m^4*Pa` (по умолчанию) | положительный вектор

`Linear density` - Плотность на единицу длины
`19` `kg/m` (по умолчанию) | положительная скалярная величина

`Segment linear density [B,...,F]` - Плотность на единицу длины для каждого сегмента
`[20, 19, 18]` `kg/m` (по умолчанию) | положительный вектор

`Material density` - Плотность материала
`7.8e3` `kg/m^3` (по умолчанию) | положительная скалярная величина

`Shear modulus` - Модуль сдвига
`7.93e9` `Pa` (по умолчанию) | положительная скалярная величина

`Young's modulus` - Модуль Юнга
`200e9` `Pa` (по умолчанию) | положительная скалярная величина

`Shaft geometry` - Геометрия поперечного сечения
`Solid` (по умолчанию) | `Annular`

`Shaft outer diameter` - Наружный диаметр вала
`0.075` `m` (по умолчанию) | положительная скалярная величина

`Segment outer diameter [B,...,F]` - Наружный диаметр для каждого сегмента вала
`[.085, .075, .065]` `m` (по умолчанию) | положительный вектор

`Shaft inner diameter` - Внутренний диаметр вала
`0.05` `m` (по умолчанию) | позитвенный скаляр

`Segment inner diameter [B,...,F]` - Внутренний диаметр для каждого сегмента вала
`[.055, .05, .045]` `m` (по умолчанию) | вектор

`Damping ratio from internal losses` - коэффициент затухания материала
`0.01` (по умолчанию) | положительная скалярная величина

`Viscous friction coefficients at base (B) and follower (F)` - Коэффициенты вязкого трения
`[0, 0]` `N*m/(rad/s)` (по умолчанию) | неотрицательный вектор

`Viscous friction coefficients at each support [B1,...,F1]` - Коэффициенты вязкого трения
`[0, 0]` `N*m/(rad/s)` (по умолчанию) | неотрицательный вектор

`Initial shaft torsional deflection` - Начальное кручение вала
`0` `rad` (по умолчанию) | неотрицательной скаляром

`Initial shaft angular velocity` - Начальная скорость вращения
`0` `rpm` (по умолчанию) | неотрицательной скаляром

`Number of supports` - Количество поддержек
`2` (по умолчанию) | `3` | `4`

`Support locations relative to base (B)` - Места оказания поддержки
`[0, 1]` `m` (по умолчанию) | неотрицательный вектор увеличения

`Base (B1) mounting type` - Поддержка B1 монтажа
`Clamped` (по умолчанию) | `Pinned` | `Free` | `Bearing matrix` | `Speed-dependent bearing matrix`

`Base (B1) rotational damping [xx,yy]` - Поддержка B1 вращательного демпфирования
`[1e3, 1e3]` `N*m/(rad/s)` (по умолчанию) | вектор

`Base (B1) translational damping [xx,xy,yx,yy]` - Поддержка B1 поступательное демпфирование
`[2e4, -4.4e4, -4.4e4, 3.5e5]` `N/(m/s)` (по умолчанию) | вектор

`Base (B1) rotational stiffness [xx,yy]` - Поддержка B1 вращательная жесткость
`[1e4, 1e4]` `N*m/rad` (по умолчанию) | неотрицательный вектор

`Base (B1) translational stiffness [xx,xy,yx,yy]` - Поддержка B1 поступательная жесткость
`[1e6, -2e5, -3e5, 5e]` `N/m` (по умолчанию) | вектор

`Intermediate (I1) mounting type` - Поддержка I1 монтажа
`Clamped` (по умолчанию) | `Pinned` | `Free` | `Bearing matrix` | `Speed-dependent bearing matrix`

`Intermediate (I1) rotational damping [xx,yy]` - Поддержка I1 вращательного демпфирования
`[1e3, 1e3]` `N*m/(rad/s)` (по умолчанию) | вектор

`Intermediate (I1) translational damping [xx,xy,yx,yy]` - Поддержка I1 поступательное демпфирование
`[2e4, -4.4e4, -4.4e4, 3.5e5]` `N/(m/s)` (по умолчанию) | вектор

`Intermediate (I1) rotational stiffness [xx,yy]` - Поддержка I1 вращательная жесткость
`[1e4, 1e4]` `N*m/rad` (по умолчанию) | неотрицательный вектор

`Intermediate (I1) translational stiffness [xx,xy,yx,yy]` - Поддержка I1 поступательная жесткость
`[1e6, -2e5, -3e5, 5e]` `N/m` (по умолчанию) | вектор

`Intermediate (I2) mounting type` - Поддержка I2 монтажа
`Clamped` (по умолчанию) | `Pinned` | `Free` | `Bearing matrix` | `Speed-dependent bearing matrix`

`Intermediate (I2) rotational damping [xx,yy]` - Поддержка I2 вращательного демпфирования
`[1e3, 1e3]` `N*m/(rad/s)` (по умолчанию) | вектор

`Intermediate (I2) translational damping [xx,xy,yx,yy]` - Поддержка I2 поступательное демпфирование
`[2e4, -4.4e4, -4.4e4, 3.5e5]` `N/(m/s)` (по умолчанию) | вектор

`Intermediate (I2) rotational stiffness [xx,yy]` - Поддержка I2 вращательная жесткость
`[1e4, 1e4]` `N*m/rad` (по умолчанию) | неотрицательный вектор

`Intermediate (I2) translational stiffness [xx,xy,yx,yy]` - Поддержка I2 поступательная жесткость
`[1e6, -2e5, -3e5, 5e]` `N/m` (по умолчанию) | вектор

`Follower (F1) mounting type` - Поддержка F1 монтажа
`Clamped` (по умолчанию) | `Pinned` | `Free` | `Bearing matrix` | `Speed-dependent bearing matrix`

`Follower (F1) rotational damping [xx,yy]` - Поддержка F1 вращательного демпфирования
`[1e3, 1e3]` `N*m/(rad/s)` (по умолчанию) | вектор

`Follower (F1) translational damping [xx,xy,yx,yy]` - Поддержка F1 поступательное демпфирование
`[2e4, -4.4e4, -4.4e4, 3.5e5]` `N/(m/s)` (по умолчанию) | вектор

`Follower (F1) rotational stiffness [xx,yy]` - Поддержка F1 вращательная жесткость
`[1e4, 1e4]` `N*m/rad` (по умолчанию) | неотрицательный вектор

`Follower (F1) translational stiffness [xx,xy,yx,yy]` - Поддержка F1 поступательная жесткость
`[1e6, -2e5, -3e5, 5e]` `N/m` (по умолчанию) | вектор

`Bearing speed [s1,...,sS]` - Поддержка вращения опорного подшипника
`[200, 500, 1500]` `rpm` (по умолчанию) | неотрицательный вектор

`Damping constant proportional to mass` - Демпфирование постоянной α
`10` `1/s` (по умолчанию) | положительная скалярная величина

`Damping constant proportional to stiffness` - Константа демпфирования β
`1e-8` `s` (по умолчанию) | положительная скалярная величина

`Rigid masses concentrically attached to shaft` - Тип жестких масс, прикрепленных к валу
`None` (по умолчанию) | `Point mass` | `Disk`

`Rigid mass distances from base (B)` - Расположение твердых масс вдоль вала на расстоянии от базового узла
`0.5` `m` (по умолчанию) | неотрицательный скаляр или вектор

`Rigid masses` - Масса жестких масс, концентрически присоединенных к валу
`2` `kg` (по умолчанию) | положительная скалярная величина или вектор

`Rigid mass polar moments of inertia about shaft axis` - Полярные моменты инерции вокруг оси вала
`0.050` `kg*m^2` (по умолчанию) | положительная скалярная величина или вектор

`Static unbalances that excite bending` - Возбуждение статических дисбалансов
`[.01, .01]` `m*kg` (по умолчанию) | неотрицательный вектор