Модель автомобиля, подобного рулевому транспортному средству
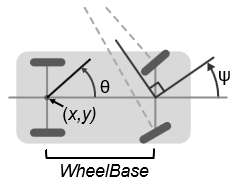
ackermannKinematics создает модель автомобиля, подобную модели транспортного средства, которая использует рулевое управление Ackermann. Эта модель представляет транспортное средство с двумя осями, разделенными расстоянием, WheelBase. Состояние транспортного средства определяется как четырехэлементный вектор [x y theta psi] с глобальным xy -положением, заданным в метрах. Положение xy расположено в середине задней оси. Курс транспортного средства, theta и угол поворота psi заданы в радианах. Курс транспортного средства определяется в центре задней оси. Углы заданы в радианах. Чтобы вычислить состояния производной по времени для модели, используйте derivative функция с входными командами управления и текущим состоянием робота.
kinematicModel = ackermannKinematics
kinematicModel = ackermannKinematics(Name,Value)
WheelBase - Расстояние между передней и задней осями1 (по умолчанию) | положительный числовой скалярОснова колеса относится к расстоянию между передней и задней осями, указанному в метрах.
VehicleSpeedRange - Область значений скоростей колес транспортных средств[-Inf Inf] (по умолчанию) | двухэлементный векторТранспортное средство скорости области значений является двухэлементным вектором, который обеспечивает минимальную и максимальную скорости транспортного средства, [MinSpeed MaxSpeed], заданную в метрах в секунду.
derivative | Производная по времени от состояния транспортного средства |
Этот пример показывает, как смоделировать различные модели кинематики робота в окружении и сравнить их.
Задайте мобильных роботов с кинематическими ограничениями
Существует ряд способов смоделировать кинематику мобильных роботов. Все диктуют, как скорости колеса связаны с состоянием робота: [x y theta], как xy-координаты и курс робота, theta, в радианах.
Одноколесная кинематическая модель
Самый простой способ представления кинематики мобильного робота автомобиля - это одноколесная модель, которая имеет скорость колеса, заданную вращением вокруг центральной оси, и может поворачиваться вокруг своей оси z. Кинематические модели как дифференциального привода, так и велосипеда сводятся к одноколесной кинематике, когда входы в качестве скорости движения транспортного средства и скорости движения транспортного средства и другие ограничения не рассматриваются.
unicycle = unicycleKinematics("VehicleInputs","VehicleSpeedHeadingRate");
Дифференциально-приводная кинематическая модель
Модель дифференциального привода использует заднюю ведущую ось, чтобы контролировать и скорость транспортного средства, и скорость напора. Колеса на ведущей оси могут вращаться в обоих направлениях. Поскольку большинство мобильных роботов имеют некоторый интерфейс с командами низкоуровневого колеса, эта модель снова будет использовать транспортное средство скорость и скорость курса в качестве входных параметров для упрощения управления транспортного средства.
diffDrive = differentialDriveKinematics("VehicleInputs","VehicleSpeedHeadingRate");
Чтобы дифференцировать поведение от одноколесной модели, добавьте ограничение скорости вращения колеса к дифференциально-приводной кинематической модели
diffDrive.WheelSpeedRange = [-10 10]*2*pi;
Велосипедная кинематическая модель
Модель велосипеда относится к роботу как к автомобилоподобной модели с двумя осями: задней ведущей осью и передней осью, которая поворачивается вокруг оси Z. Модель велосипеда работает при предположении, что колеса на каждой оси могут быть смоделированы как одно, центрированное колесо, и что курс переднего колеса может быть непосредственно установлен, как велосипед.
bicycle = bicycleKinematics("VehicleInputs","VehicleSpeedHeadingRate","MaxSteeringAngle",pi/8);
Другие модели
Кинематическая модель Ackermann является модифицированной моделью, подобной автомобилю, которая принимает рулевое управление Ackermann. В большинстве автомобильных транспортных средств передние колеса не поворачиваются вокруг одной оси, а вместо этого включают несколько другие оси, чтобы убедиться, что они ездят по концентрическим кругам вокруг центра транспортного средства поворота. Это различие угла поворота называется Ackermann рулевое управление, и обычно обеспечивается механизмом в фактических транспортных средствах. С точки зрения кинематики транспортного средства и колеса его можно применить, рассматривая угол поворота руля как вход скорости.
carLike = ackermannKinematics;
Настройка параметров симуляции
Эти мобильные роботы будут следовать набору путевых точек, который разработан, чтобы показать некоторые различия, вызванные различной кинематикой.
waypoints = [0 0; 0 10; 10 10; 5 10; 11 9; 4 -5]; % Define the total time and the sample rate sampleTime = 0.05; % Sample time [s] tVec = 0:sampleTime:20; % Time array initPose = [waypoints(1,:)'; 0]; % Initial pose (x y theta)
Создайте контроллер Транспортного средства
Транспортные средства следуют за набором путевых точек с помощью контроллера Pure Pursuit. Учитывая набор путевых точек, текущее состояние робота и некоторые другие параметры, контроллер выходы транспортного средства скорость и скорость курса.
% Define a controller. Each robot requires its own controller controller1 = controllerPurePursuit("Waypoints",waypoints,"DesiredLinearVelocity",3,"MaxAngularVelocity",3*pi); controller2 = controllerPurePursuit("Waypoints",waypoints,"DesiredLinearVelocity",3,"MaxAngularVelocity",3*pi); controller3 = controllerPurePursuit("Waypoints",waypoints,"DesiredLinearVelocity",3,"MaxAngularVelocity",3*pi);
Симулируйте модели с помощью решателя ОДУ
Модели моделируются с помощью derivative функция для обновления состояния. Этот пример использует решатель для обыкновенных дифференциальных уравнений (ОДУ), чтобы сгенерировать решение. Другим способом является обновление состояния с помощью цикла, как показано на Пути Following for a Робота с дифференциальным приводом.
Поскольку решатель ОДУ требует, чтобы все выходы были предоставлены как один выход, контроллер чистого преследования должен быть обернут в функцию, которая выводит линейную скорость и скорость вращения курса как один выход. Пример помощника, exampleHelperMobileRobotController, используется для этой цели. Пример помощника также гарантирует, что робот останавливается, когда он находится в заданном радиусе цели.
goalPoints = waypoints(end,:)'; goalRadius = 1;
ode45 вызывается один раз для каждого типа модели. Производная функция вычисляет выходы с начальным состоянием, заданным initPose. Каждая производная принимает соответствующий объект кинематической модели, текущее положение робота и выход контроллера в этом положении.
% Compute trajectories for each kinematic model under motion control
[tUnicycle,unicyclePose] = ode45(@(t,y)derivative(unicycle,y,exampleHelperMobileRobotController(controller1,y,goalPoints,goalRadius)),tVec,initPose);
[tBicycle,bicyclePose] = ode45(@(t,y)derivative(bicycle,y,exampleHelperMobileRobotController(controller2,y,goalPoints,goalRadius)),tVec,initPose);
[tDiffDrive,diffDrivePose] = ode45(@(t,y)derivative(diffDrive,y,exampleHelperMobileRobotController(controller3,y,goalPoints,goalRadius)),tVec,initPose);Графическое изображение результатов
Результаты решателя ОДУ можно легко просмотреть на одном графике с помощью plotTransforms визуализировать результаты всех траекторий сразу.
Выходы положения должны быть сначала преобразованы в индексированные матрицы переводов и кватернионов.
unicycleTranslations = [unicyclePose(:,1:2) zeros(length(unicyclePose),1)]; unicycleRot = axang2quat([repmat([0 0 1],length(unicyclePose),1) unicyclePose(:,3)]); bicycleTranslations = [bicyclePose(:,1:2) zeros(length(bicyclePose),1)]; bicycleRot = axang2quat([repmat([0 0 1],length(bicyclePose),1) bicyclePose(:,3)]); diffDriveTranslations = [diffDrivePose(:,1:2) zeros(length(diffDrivePose),1)]; diffDriveRot = axang2quat([repmat([0 0 1],length(diffDrivePose),1) diffDrivePose(:,3)]);
Затем набор всех преобразований можно построить и просмотреть сверху. Пути одноколесных, велосипедных и дифференциально-приводных роботов красные, синие и зеленые, соответственно. Чтобы упростить график, покажите только каждый десятый выход.
figure plot(waypoints(:,1),waypoints(:,2),"kx-","MarkerSize",20); hold all plotTransforms(unicycleTranslations(1:10:end,:),unicycleRot(1:10:end,:),'MeshFilePath','groundvehicle.stl',"MeshColor","r"); plotTransforms(bicycleTranslations(1:10:end,:),bicycleRot(1:10:end,:),'MeshFilePath','groundvehicle.stl',"MeshColor","b"); plotTransforms(diffDriveTranslations(1:10:end,:),diffDriveRot(1:10:end,:),'MeshFilePath','groundvehicle.stl',"MeshColor","g"); view(0,90)

Симулируйте модель мобильного робота, которая использует рулевое управление Ackermann с ограничениями на его угол поворота. Во время симуляции модель сохраняет максимальный угол поворота руля после достижения предела поворота руля. Чтобы увидеть эффект насыщения рулевого управления, вы сравниваете траекторию двух роботов, один с ограничениями на угол рулевого управления, а другой без каких-либо ограничений рулевого управления.
Определите модель
Задайте кинематическую модель Аккермана. В этой модели, подобной автомобилю, передние колеса расположены на заданном расстоянии друг от друга. Чтобы они включали концентрические круги, колеса имеют разные углы поворота. При повороте передние колеса получают вход рулевого управления как скорость изменения угла поворота рулевого управления.
carLike = ackermannKinematics;
Настройка параметров симуляции
Установите мобильного робота, чтобы следовать постоянной линейной скорости и получить постоянную скорость рулевого управления в качестве входных параметров. Симулируйте ограниченного робота в течение более длительного периода, чтобы продемонстрировать насыщение рулевого управления.
velo = 5; % Constant linear velocity psidot = 1; % Constant left steering rate % Define the total time and sample rate sampleTime = 0.05; % Sample time [s] timeEnd1 = 1.5; % Simulation end time for unconstrained robot timeEnd2 = 10; % Simulation end time for constrained robot tVec1 = 0:sampleTime:timeEnd1; % Time array for unconstrained robot tVec2 = 0:sampleTime:timeEnd2; % Time array for constrained robot initPose = [0;0;0;0]; % Initial pose (x y theta phi)
Создайте структуру опций для решателя ОДУ
В этом примере вы передаете options структура как аргумент решателя ОДУ. The options структура содержит информацию о пределе угла поворота руля. Как создать options структура, используйте Events опция odeset и созданная функция события, detectSteeringSaturation. detectSteeringSaturation устанавливает максимальный угол поворота руля равным 45 степеням.
Описание того, как определить detectSteeringSaturation, см. Define Event Function в конце этого примера.
options = odeset('Events',@detectSteeringSaturation);Симулируйте модель с помощью решателя ОДУ
Далее вы используете derivative функция и решатель ОДУ, ode45, чтобы решить модель и сгенерировать решение.
% Simulate the unconstrained robot [t1,pose1] = ode45(@(t,y)derivative(carLike,y,[velo psidot]),tVec1,initPose); % Simulate the constrained robot [t2,pose2,te,ye,ie] = ode45(@(t,y)derivative(carLike,y,[velo psidot]),tVec2,initPose,options);
Обнаружение насыщения рулевого управления
Когда модель достигает предела управления, она регистрирует временную метку события. Время достижения предела сохранено в te.
if te < timeEnd2 str1 = "Steering angle limit was reached at "; str2 = " seconds"; comp = str1 + te + str2; disp(comp) end
Steering angle limit was reached at 0.785 seconds
Симулируйте ограниченного робота с новыми начальными условиями
Теперь используйте состояние ограниченного робота перед прекращением интегрирования в качестве начального условия для второй симуляции. Измените вектор входа, чтобы представлять насыщение рулевого управления, то есть установите скорость рулевого управления равного нуля.
saturatedPsiDot = 0; % Steering rate after saturation cmds = [velo saturatedPsiDot]; % Command vector tVec3 = te:sampleTime:timeEnd2; % Time vector pose3 = pose2(length(pose2),:); [t3,pose3,te3,ye3,ie3] = ode45(@(t,y)derivative(carLike,y,cmds), tVec3,pose3, options);
Постройте график результатов
Постройте график траектории робота с помощью plot и данные, хранящиеся в pose.
figure(1) plot(pose1(:,1),pose1(:,2),'--r','LineWidth',2); hold on; plot([pose2(:,1); pose3(:,1)],[pose2(:,2);pose3(:,2)],'g'); title('Trajectory X-Y') xlabel('X') ylabel('Y') legend('Unconstrained robot','Constrained Robot','Location','northwest') axis equal

Робот без ограничений следует по спиральной траектории с уменьшающимся радиусом кривизны, а робот с ограничениями - по круговой траектории с постоянным радиусом кривизны после достижения предела рулевого управления.
Задайте функцию события
Установите функцию события таким образом, чтобы интегрирование заканчивалось, когда 4-е состояние, theta, равно максимальному углу поворота.
function [state,isterminal,direction] = detectSteeringSaturation(t,y) maxSteerAngle = 0.785; % Maximum steering angle (pi/4 radians) state(4) = (y(4) - maxSteerAngle); % Saturation event occurs when the 4th state, theta, is equal to the max steering angle isterminal(4) = 1; % Integration is terminated when event occurs direction(4) = 0; % Bidirectional termination end
[1] Линч, Кевин М. и Фрэнк С. Парк. Современная робототехника: Механика, Планирование и Контроль 1 эд. Кембридж, Массачусетс: Cambridge University Press, 2017.
У вас есть измененная версия этого примера. Вы хотите открыть этот пример с вашими правками?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.